동적 계획법 (Dynamic Programming - DP)
 핵심 개념
핵심 개념
DP 이전단계에서 구했던 최적의 값과, 현재상황에서 구한 값을 비교하여 더 최적의 값을 찾는 알고리즘이다.
 DP가 필요한 이유
DP가 필요한 이유
많은 알고리즘 문제는 큰 문제를 작은 문제로 쪼개서 해결합니다. 하지만 단순히 재귀로 풀면 같은 계산을 수십, 수백 번 반복하게 됩니다.
예를 들어, fibonacci(5)를 재귀로 계산하면:
fib(5)
/ \
fib(4) fib(3) ← fib(3)이 여기서 1번
/ \ / \
fib(3) fib(2) fib(2) fib(1)
/ \ ↑ ↑
fib(2) fib(1) | |
└───────┴─── 중복 계산 발생!
fib(3)은 2번, fib(2)는 3번 계산됩니다.
큰 숫자일수록 중복은 기하급수적으로 증가합니다!
Plain Text
복사
DP의 핵심 아이디어: 한 번 계산한 결과를 저장(메모)해두고, 다시 필요할 때 재사용하자!
동적 계획법의 세 가지 핵심 특징
1. 중복 부분 문제 (Overlapping Subproblems)
같은 작은 문제가 여러 번 반복해서 등장합니다.
예시: fib(5)를 계산할 때 fib(3), fib(2)가 여러 번 등장
→ 한 번만 계산하고 저장하면, 나머지는 그냥 꺼내 쓰면 됨!
Plain Text
복사
2. 최적 부분 구조 (Optimal Substructure)
큰 문제의 최적해가 작은 문제들의 최적해로 구성됩니다.
예시: "15원 거스름돈의 최소 동전 개수"
= min(
"14원의 최소 개수 + 1원 동전 1개",
"10원의 최소 개수 + 5원 동전 1개",
...
)
→ 작은 문제(14원, 10원)의 최적해를 알면, 큰 문제(15원)도 풀 수 있음!
Plain Text
복사
3. Memoization / Tabulation
계산한 결과를 테이블에 저장해서 재사용합니다.
**메모이제이션(Top-Down)**과 **타뷸레이션(Bottom-Up)**은 DP를 코드로 옮길 때 사용하는 **'양대 구현 방식'**일 뿐입니다.
Memoization
방식: Top-Down (하향식)
구현: 재귀 (Recursion)
큰 문제를 해결하기 위해 작은 문제를 호출하다가, 이미 계산한 적 있는 값이라면 계산하지 않고 저장된 값을 반환하는 방식입니다.
•
특징:
◦
필요한 부분만 계산(Lazy Evaluation): 문제 해결에 필요 없는 하위 문제는 계산하지 않습니다.
◦
캐싱(Caching): 이전에 계산한 값을 메모리(배열, 해시맵 등)에 '메모'해 둡니다.
◦
단점: 재귀 호출의 깊이가 깊어지면 스택 오버플로우(Stack Overflow)가 발생할 수 있으며, 함수 호출 오버헤드가 있습니다.
Tabulation
방식: Bottom-Up (상향식)
구현: 반복문 (Iteration / Loop)
가장 작은 문제(기저 사례)부터 시작해서 테이블(배열)을 차례대로 채워 나가며 최종적으로 큰 문제를 해결하는 방식입니다.
•
특징:
◦
모든 부분 계산(Eager Evaluation): 테이블의 처음부터 끝까지 순차적으로 다 채웁니다.
◦
테이블 채우기: dp[0], dp[1]... 순서로 값을 채워 나가므로 타뷸레이션이라 부릅니다.
◦
장점: 재귀 호출이 없어 스택 오버플로우 위험이 없고, 일반적으로 메모이제이션보다 성능이 약간 더 빠릅니다. (CPU 캐시 지역성 활용 유리)
◦
단점: 문제 해결에 필요 없는 하위 문제까지 모두 계산할 수도 있습니다
// Top-down (재귀 + 메모)
int memo[100];
int fib_memo(int n)
{
if (n <= 1)
return n;
if (memo[n] != 0)
return memo[n]; // 이미 계산했으면 바로 리턴!
return memo[n] = fib_memo(n-1) + fib_memo(n-2);
}
// Bottom-up (반복문 + 테이블)
int fib_dp(int n)
{
vector<int> dp(n+1);
dp[0] = 0; dp[1] = 1;
for (int i = 2; i <= n; i++)
dp[i] = dp[i-1] + dp[i-2]; // 작은 것부터 차례로 계산
return dp[n];
}
C++
복사
 DP의 시간복잡도 개선 원리
DP의 시간복잡도 개선 원리
재귀 (중복 계산):
- fib(5): 15번의 함수 호출
- fib(10): 177번의 함수 호출
- fib(40): 약 20억 번의 함수 호출! 💀
→ 시간복잡도: O(2^n) - 지수 시간
DP (중복 제거):
- fib(5): 5번의 계산 (각 숫자당 1번)
- fib(10): 10번의 계산
- fib(40): 40번의 계산
→ 시간복잡도: O(n) - 선형 시간
결론: 중복 계산을 제거하면 지수 → 선형으로 극적 개선!
Plain Text
복사
 그래프 탐색 vs 동적 계획법
그래프 탐색 vs 동적 계획법
그래프 탐색 (BFS/DFS)
위 문제를 해결하기 위한 대표적인 알고리즘 세가지를 고려해 볼 수 있다.
1. 모든 경우의 수를 다 해볼것인가? 브루트포스(DFS,BFS)
Plain Text
복사
DP의 장점
2. 최적의 해를 향상 그리기에 찾는다. 그리디 알고리즘
과거 선택에대한 고려가 전혀 없어 미래를 선택하는 부분도 전혀 고려를 하지 않고 현재의
한때 선택한다.
3. DP 이전단계에서 구했던 최적의 값과, 현재상황에서 구한 값을 비교하여 더 최적의 값을 찾는 알고리즘이다.
Plain Text
복사
// factorial dp, 재귀함수 비교 예시
#include <iostream>
#include <vector>
int factorial(int n)
{
if (n <= 1)
return 1;
//int result = n * factorial(n - 1);
//return result;
return n * factorial(n - 1);
}
int factorial_dp(int n)
{
if (n < 0)
return -1;
std::vector<int> dp(n + 1);
dp[0] = 1;
for (size_t i = 1; i < n + 1; i++)
dp[i] = dp[i - 1] * i;
return dp[n];
}
int main()
{
int fact = factorial(5);
fact = factorial_dp(5);
return 0;
}
C++
복사
 동전 문제 (Coin Change Problem)
동전 문제 (Coin Change Problem)
문제 상황
또 다른 예로 앞서 풀어봤던 문제죄에 거스름돈 문제가 있다.
화폐단위: 500원, 100원, 50원, 10원
손님이 받을 개수: 2개, 2개, 1개, 1개
1260원을 만드는 경우 이것 또한 그리디 알고리즘의 하나로 볼 수 있다.
Plain Text
복사
그리디 알고리즘의 한계
3,4,5원의 동전을 가지고 15원을 만들어보라고 가정해보자.
그리디로 해결하면:
•
5원 × 3개 = 15원 
•
하지만 다른 조합도 가능: 3원 × 5개 = 15원
 DP 테이블로 문제 해결
DP 테이블로 문제 해결
기본 DP 문제 설정
위문제를 DP로 풀어보자
정확하고 대표적인 기본 DP 문제이다. dp 테이블을 만들어서 문제를 해결하면 된다.
만들어야 할 테이블의 크기를 정해준다. 금액보다 +1 한개 크게 만들어주면 된다.
 DP 테이블 설계 원리
DP 테이블 설계 원리
DP 테이블을 만들 때는 다음을 정의해야 합니다:
1. 테이블의 의미: dp[i] = i원을 만들 수 있는 경우의 수
2. 초기값: dp[0] = 1 (0원을 만드는 방법은 "아무것도 선택 안함" 1가지)
3. 테이블 크기: 목표 금액 + 1 (0원부터 시작하므로)
vector<int> dp(amount + 1, 0); // 모두 0으로 초기화
dp[0] = 1; // 0원은 1가지 방법 (기저 조건)
C++
복사
3원 동전만 사용하는 경우
3원의 동전만 가지고 15원의 거스름을 만드는 경우의수를 테이블로 만들어보자
단계별 계산 과정:
dp[0] = 1 (초기값)
dp[3] = dp[3-3] = dp[0] = 1 (3원 1개)
dp[6] = dp[6-3] = dp[3] = 1 (3원 2개)
dp[9] = dp[9-3] = dp[6] = 1 (3원 3개)
dp[12] = dp[12-3] = dp[9] = 1 (3원 4개)
dp[15] = dp[15-3] = dp[12] = 1 (3원 5개)
나머지는 모두 0 (3원으로 만들 수 없음)
| 금액 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10| 11| 12| 13| 14| 15|
|------|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3원 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
↑ ↑ ↑ ↑ ↑
초기값 3원×1개 3원×2개 3원×3개 3원×5개
Plain Text
복사
3원과 4원 동전을 함께 사용하는 경우
이제 4원 동전을 추가해봅시다. 핵심: 이전 결과(3원만)를 유지하면서 새로운 경우를 더해갑니다.
4원 동전 추가 후 변화:
dp[4] = dp[4] + dp[4-4] = 0 + dp[0] = 0 + 1 = 1
↑ ↑
기존값 4원 1개 사용
dp[7] = dp[7] + dp[7-4] = 0 + dp[3] = 0 + 1 = 1
↑ ↑
기존값 "3원 1개" + "4원 1개"
dp[8] = dp[8] + dp[8-4] = 0 + dp[4] = 0 + 1 = 1
↑
"4원 2개"
dp[12] = dp[12] + dp[12-4] = 1 + dp[8] = 1 + 1 = 2
↑ ↑
3원×4개(기존) 4원×3개(새로운)
| 금액 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10| 11| 12| 13| 14| 15|
|------|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3원 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 3,4원| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 1 | 1 | 2 |
↑ ↑
4원 추가 3원×4 + 4원×3
2가지 방법!
Plain Text
복사
금액 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
3 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
3,4 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 1 | 1 | 2 |
3,4,5 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 4 |
거스름돈이 4원이 만들어질때까지는 3원까지의 조합과 동일하다.
 DP 알고리즘 단계별 분석
DP 알고리즘 단계별 분석
 DP 점화식 도출 - 핵심 원리
DP 점화식 도출 - 핵심 원리
점화식 dp[i] += dp[i - coin]이 왜 성립하는지 깊이 이해해봅시다.
점화식의 의미
1차원 배열 기반
dp[i] += dp[i - coin]
↑ ↑
| └─ 현재 동전을 1개 사용한 후 남은 금액을 만드는 경우의 수
└────────── 기존 경우의 수에 "추가"
2차원 배열 기반
dp[i][j] = dp[i - 1][j] + dp[i][j - coin];
Plain Text
복사
왜 '='가 아니라 '+='인가?
중요: 우리는 동전을 하나씩 순차적으로 추가하면서 테이블을 업데이트합니다.
예시: 7원을 만드는 경우
1단계 (3원 동전만):
dp[7] = 0 (3원으로는 7원을 만들 수 없음)
2단계 (4원 동전 추가):
dp[7] = dp[7] + dp[7-4]
= 0 + dp[3]
= 0 + 1 = 1
↑ ↑
기존값 새로운 방법 (3원 1개 + 4원 1개)
만약 '='를 사용했다면:
dp[7] = dp[3] = 1 (기존 값 0이 사라짐, 하지만 여기선 기존값이 0이라 상관없음)
더 명확한 예시 - 12원:
3원만: dp[12] = 1 (3원×4개)
4원 추가: dp[12] += dp[8] = 1 + 1 = 2
↑ ↑
기존 새로운
'='를 썼다면 기존 방법(3원×4개)이 사라집니다!
Plain Text
복사
점화식이 작동하는 수학적 원리
질문: "15원을 만드는 경우의 수는?"
생각의 흐름:
1. 5원 동전을 "사용 안함" → dp[15] (5원 추가 전 값)
2. 5원 동전을 "1개 사용" → 남은 10원을 만드는 경우의 수 = dp[10]
3. 5원 동전을 "2개 사용" → 남은 5원을 만드는 경우의 수 = dp[5]
4. 5원 동전을 "3개 사용" → 남은 0원을 만드는 경우의 수 = dp[0]
핵심 통찰:
"5원을 1개 이상 사용하는 모든 경우" = dp[10] (1개 사용 후 남은 금액)
왜냐하면:
- 5원을 정확히 1개 쓰는 경우는 dp[10]에 5원 동전이 없는 조합들
- 5원을 2개 이상 쓰는 경우는 dp[10]에 5원 동전이 포함된 조합들
- dp[10]을 계산할 때 이미 "5원을 또 쓸 수 있는지" 고려했기 때문!
따라서:
dp[15] = dp[15](5원 안씀) + dp[10](5원 1개 이상 씀)
Plain Text
복사
동전 순서가 중요한 이유
// 동전별로 순차 처리 (올바른 방법)
for (int coin : coins) // 각 동전에 대해
for (int i = coin; i <= amount; i++) // 모든 금액 업데이트
dp[i] += dp[i - coin];
// 만약 순서를 바꾸면?
for (int i = 0; i <= amount; i++) // 각 금액에 대해
for (int coin : coins) // 모든 동전 시도
dp[i] += dp[i - coin];
// 문제: (3원, 4원)과 (4원, 3원)을 다른 경우로 중복 계산!
C++
복사
왜 동전별로 처리해야 하는가?
•
동전의 "순서"를 무시하고 "조합"만 세기 위해서
•
3원 → 4원 순서로 처리하면, 4원을 추가할 때 3원이 이미 고려됨
•
따라서 (3원, 4원) = (4원, 3원) 으로 동일하게 취급됨
0+0 은 0 이기 때문에 (3,4) 조합으로 5원을 거슬러 줄 수 없다
dp[i] += dp[i - coin] // 핵심 점화식
Plain Text
복사
4원 동전 추가 후 변화
4원 부터는 달라진다.
| 금액 | 0 | 1 | 2 | 3 | 4 |
|------|---|---|---|---|---|
| 3원 | 1 | 0 | 0 | 1 | 0 |
| 3,4원| 1 | 0 | 0 | 1 | 1 |
5원의 경우에는 3,4원으로 만들 수 있는 경우의수가 없다.
그렇다면 3,4원으로 5원을 거슬러 줄 경우에는 4원을 내주고 1원을 거슬러 줄 수 있는 경우의 조합이 있을 것이 불 수 있다.
| 금액 | 0 | 1 | 2 | 3 | 4 | 5 |
|------|---|---|---|---|---|---|
| 3원 | 1 | 0 | 0 | 1 | 0 | 0 |
| 3,4원| 1 | 0 | 0 | 1 | 1 | 0 |
|3,4,5 | 1 | 0 | 0 | 1 | 1 | 1 |
Plain Text
복사
 DP 구현 코드
DP 구현 코드
#include <iostream>
#include <vector>
using namespace std;
int main()
{
// 동전 집합과 목표 금액
vector<int> coins = {3, 4, 5};
int amount = 15;
// DP 테이블 초기화: (동전 개수+1) x (금액+1)
vector<vector<int>> dp(coins.size() + 1, vector<int>(amount + 1, 0));
dp[0][0] = 1; // 아무 동전도 사용하지 않고 0원을 만드는 경우 1가지
// DP 채우기
for (int i = 1; i <= coins.size(); i++) // 각 동전별
{
int coin = coins[i - 1];
for (int j = 0; j <= amount; j++)
{
if (j < coin)
dp[i][j] = dp[i - 1][j]; // 해당 동전을 못 쓰는 경우
else
dp[i][j] = dp[i - 1][j] + dp[i][j - coin]; // 점화식
}
}
// 결과 출력
cout << "DP 테이블 (행: 동전개수, 열: 금액)" << endl;
for (int i = 0; i <= coins.size(); i++)
{
for (int j = 0; j <= amount; j++)
cout << dp[i][j] << " ";
cout << endl;
}
cout << "\n" << amount << "원을 만드는 경우의 수: " << dp[coins.size()][amount] << endl;
return 0;
}
GLSL
복사
#include <iostream>
#include <vector>
#include <algorithm>
#include <climits>
using namespace std;
int main()
{
// 동전 집합과 목표 금액
vector<int> coins = {3, 4, 5};
int amount = 15;
// DP 테이블 초기화
vector<int> dp(amount + 1, 0);
dp[0] = 1; // 0원을 만드는 방법은 1가지 (아무것도 선택하지 않기)
// 각 동전에 대해
for (int coin : coins)
{
// 해당 동전부터 목표 금액까지
for (int i = coin; i <= amount; i++)
{
dp[i] += dp[i - coin]; // 점화식
}
}
// 결과 출력
if (dp[amount] == 0)
{
cout << "해당 금액을 만들 수 없습니다." << endl;
}
else
{
cout << amount << "원을 만들기 위한 최소 동전 개수: " << dp[amount] << endl;
}
return 0;
}
C++
복사
 DP 실행 과정 시뮬레이션
DP 실행 과정 시뮬레이션
3원 동전 처리
coin = 3일 때:
i=3: dp[3] += dp[0] = 0 + 1 = 1
i=6: dp[6] += dp[3] = 0 + 1 = 1
i=9: dp[9] += dp[6] = 0 + 1 = 1
...
Plain Text
복사
4원 동전 추가
coin = 4일 때:
i=4: dp[4] += dp[0] = 0 + 1 = 1
i=7: dp[7] += dp[3] = 0 + 1 = 1
i=8: dp[8] += dp[4] = 0 + 1 = 1
...
Plain Text
복사
5원 동전 추가
coin = 5일 때:
i=5: dp[5] += dp[0] = 0 + 1 = 1
i=8: dp[8] += dp[3] = 1 + 1 = 2 (3+5 또는 4+4)
i=10: dp[10] += dp[5] = 1 + 1 = 2
...
Plain Text
복사
 DP 테이블 완성 과정
DP 테이블 완성 과정
최종 DP 테이블
결과적으로 이것들은 패턴이 보이기 시작한다.
| 금액 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10| 11| 12| 13| 14| 15|
|------|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3원 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 3,4원| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 1 | 1 | 2 |
7원의 경우 (현재 동전) 추가되지전 거슬러 줄 수 있는 경우의수 0) + (4원 거슬러주고 남은 3원 거슬러 줄 수 있는 경우의수 1) = 1이 된다.
Plain Text
복사
 DP의 핵심 원리
DP의 핵심 원리
1. 상태 정의
dp[i] = i원을 만들 수 있는 경우의 수
C++
복사
2. 초기값 설정
dp[0] = 1; // 0원을 만드는 방법은 1가지
C++
복사
3. 점화식
dp[i] += dp[i - coin]; // 현재 동전을 사용해서 만드는 경우
C++
복사
4. 계산 순서
•
동전별로 순차 처리
•
각 동전에 대해 해당 동전 값부터 목표까지 계산
 다양한 DP 문제 유형
다양한 DP 문제 유형
1. 동전 교환 문제 변형들
•
최소 동전 개수: dp[i] = min(dp[i], dp[i-coin] + 1)
•
경우의 수: dp[i] += dp[i-coin]
•
가능 여부: dp[i] = dp[i] || dp[i-coin]
2. 배낭 문제 (Knapsack)
dp[i][w] = max(dp[i-1][w], dp[i-1][w-weight[i]] + value[i]);
C++
복사
3. 피보나치 수열
dp[i] = dp[i-1] + dp[i-2];
C++
복사
 DP 설계 체크리스트
DP 설계 체크리스트
 DP 적용 가능 조건
DP 적용 가능 조건
1.
최적 부분 구조: 작은 문제의 최적해가 큰 문제의 최적해에 포함
2.
중복 부분 문제: 같은 하위 문제가 여러 번 등장
3.
무후효성: 현재 상태가 미래에만 영향, 과거와 독립
 DP 구현 단계
DP 구현 단계
1.
상태 정의: dp[i]가 무엇을 의미하는지 명확히
2.
점화식 도출: 상태 간의 관계식 설정
3.
기저 조건: 초기값 설정
4.
계산 순서: Bottom-up 또는 Top-down
 연습 문제
연습 문제
1.
계단 오르기: 1칸 또는 2칸씩 올라갈 수 있을 때 n번째 계단에 도달하는 방법의 수
2.
최장 증가 부분 수열: 배열에서 증가하는 부분 수열의 최대 길이
3.
편집 거리: 두 문자열을 같게 만들기 위한 최소 편집 횟수
4.
0-1 배낭 문제: 용량 제한이 있는 배낭에 최대 가치로 물건 담기
 피보나치 수열 DP 분석
피보나치 수열 DP 분석
 문제 정의
문제 정의
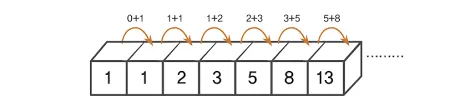
피보나치 수열: F(n) = F(n-1) + F(n-2), F(0) = 0, F(1) = 1
수열: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...
F(10) = 55를 구해보자
Plain Text
복사
 일반 재귀 vs DP 비교
일반 재귀 vs DP 비교
일반 재귀 (비효율적)
int fibonacci_recursive(int n)
{
if (n <= 1) return n;
return fibonacci_recursive(n-1) + fibonacci_recursive(n-2);
}
// clean code
int fibonacci_recursive(int n)
{
if (n <= 1)
return n;
int n_1 = fibonacci_recursive(n - 1);
int n_2 = fibonacci_recursive(n - 2);
return n_1 + n_2;
}
문제점: F(5)를 계산할 때의 함수 호출 트리
F(5) ────────────────┐
/ \ │
F(4) F(3) ←───────┐ │
/ \ / \ │ │
F(3) F(2) F(2) F(1) │ │
/ \ / \ / \ │ │
F(2) F(1)F(1)F(0)F(1)F(0) │ │
/ \ │ │
F(1) F(0) │ │
│ │
중복 계산 현황: │ │
F(3): 2번 ─────────────────────────┘ │
F(2): 3번 ────────────────────────────┘
F(1): 5번
F(0): 3번
총 함수 호출: 15번!
int main()
{
int result = fibonacci_recursive(5);
return 0;
}
C++
복사
왜 O(2^n)인가?
각 함수는 2개의 자식 함수를 호출합니다 (n-1, n-2)
깊이(depth)별 함수 호출 수:
깊이 0: 1개 (F(5))
깊이 1: 2개 (F(4), F(3))
깊이 2: 4개 (F(3), F(2), F(2), F(1))
깊이 3: 최대 8개
...
깊이 n: 최대 2^n개
전체 호출 수 ≈ 2^0 + 2^1 + 2^2 + ... + 2^n ≈ 2^(n+1) - 1
따라서 시간복잡도: O(2^n)
실제 숫자로 보면:
F(10): 177번 호출
F(20): 21,891번 호출
F(30): 2,692,537번 호출
F(40): 331,160,281번 호출 (약 3억 번!) 💀
Plain Text
복사
DP 해결 (효율적)
int fibonacci_dp(int n)
{
vector<int> dp(n + 1);
dp[0] = 0; // 기저조건
dp[1] = 1; // 기저조건
for (int i = 2; i <= n; i++)
{
dp[i] = dp[i-1] + dp[i-2]; // 점화식
}
return dp[n];
}
시간복잡도: O(n) - 효율적!
C++
복사
 DP 테이블 구성 과정
DP 테이블 구성 과정
F(10)을 구하는 과정:
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10|
|----|---|---|---|---|---|---|---|---|---|---|---|
|dp[i]| 0 | 1 | 1 | 2 | 3 | 5 | 8 |13 |21 |34 |55 |
단계별 계산:
dp[2] = dp[1] + dp[0] = 1 + 0 = 1
dp[3] = dp[2] + dp[1] = 1 + 1 = 2
dp[4] = dp[3] + dp[2] = 2 + 1 = 3
dp[5] = dp[4] + dp[3] = 3 + 2 = 5
...
dp[10] = dp[9] + dp[8] = 34 + 21 = 55
Plain Text
복사
 완전한 피보나치 DP 구현
완전한 피보나치 DP 구현
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int n = 10; // F(10) 구하기
// DP 테이블 초기화
vector<int> dp(n + 1);
// 기저 조건
dp[0] = 0;
dp[1] = 1;
cout << "피보나치 수열 계산 과정:" << endl;
cout << "F(0) = " << dp[0] << endl;
cout << "F(1) = " << dp[1] << endl;
// Bottom-up 방식으로 계산
for (int i = 2; i <= n; i++)
{
dp[i] = dp[i-1] + dp[i-2];
//cout << "F(" << i << ") = F(" << (i-1) << ") + F(" << (i-2)
//<< ") = " << dp[i-1] << " + " << dp[i-2] << " = " << dp[i] << endl;
}
cout << "\n최종 결과: F(" << n << ") = " << dp[n] << endl;
return 0;
}
C++
복사
 배낭 문제 완전 정복 - 게임 아이템 수집하기
배낭 문제 완전 정복 - 게임 아이템 수집하기
 문제 상황: RPG 게임의 던전 탐험
문제 상황: RPG 게임의 던전 탐험
배경 스토리 
용사가 던전을 탐험하며 보스를 처치했습니다! 보상으로 귀중한 아이템들을 발견했지만, 인벤토리 용량이 한정되어 있어 모든 아이템을 가져갈 수 없습니다.
🎒 인벤토리 용량: 5칸
💎 발견한 아이템들:
┌──────────────────────────────────────────┐
│ 💍 마법반지 │ 2칸 │ 가치 3 │ 💰💰💰 │
│ ⚔️ 신검 │ 3칸 │ 가치 4 │ 💰💰💰💰 │
│ 🛡️ 용방패 │ 4칸 │ 가치 5 │ 💰💰💰💰💰 │
│ 👑 왕의왕관 │ 5칸 │ 가치 6 │ 💰💰💰💰💰💰 │
└──────────────────────────────────────────┘
❓ 문제: 인벤토리에 담을 수 있는 최대 가치는?
Plain Text
복사
 DP 테이블 설계 및 점화식
DP 테이블 설계 및 점화식
상태 정의
dp[i][w] = i번째 아이템까지 고려했을 때,
용량 w에서 얻을 수 있는 최대 가치
C++
복사
 왜 2차원 테이블이 필요한가?
왜 2차원 테이블이 필요한가?
배낭 문제는 두 가지 변수가 동시에 변합니다:
1.
어떤 아이템까지 고려했는가? (행: 아이템 인덱스)
2.
현재 남은 용량은? (열: 용량)
1차원으로는 표현 불가능한 상황:
"용량 5칸일 때 최대 가치"는
- 아이템 1개만 봤을 때: 3
- 아이템 2개 봤을 때: 7
- 아이템 3개 봤을 때: 7
→ 용량이 같아도 고려한 아이템에 따라 답이 다름!
따라서 dp[아이템수][용량] 2차원 필요!
Plain Text
복사
점화식 - 선택의 논리
dp[i][w] = max
(
dp[i-1][w], // 선택 1: 현재 아이템을 선택하지 않는 경우
dp[i-1][w-weight[i]] + value[i] // 선택 2: 현재 아이템을 선택하는 경우
)
C++
복사
점화식의 의미를 깊이 파헤치기
상황: 마법반지(2칸, 가치3)와 신검(3칸, 가치4)이 있고,
현재 용량 5칸에서 신검을 고려 중
질문: "신검을 넣을까, 말까?"
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
선택 1: 신검을 넣지 않는다
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
dp[2][5] = dp[1][5] // 이전 아이템까지의 최선
= 3 // 마법반지만 넣은 상태 유지
🎒 [💍 반지(2칸)] [빈공간 3칸] → 가치 3
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
선택 2: 신검을 넣는다
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
dp[2][5] = dp[1][5-3] + 4 // 신검(3칸) 넣으면 남은 2칸에서 최선 + 신검 가치
= dp[1][2] + 4
= 3 + 4 = 7
↑
"용량 2칸일 때 마법반지까지 고려한 최대 가치"
🎒 [💍 반지(2칸)] [⚔️ 신검(3칸)] → 가치 7
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
결론: max(3, 7) = 7 선택!
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
Plain Text
복사
핵심 통찰: 왜 dp[i-1][w-weight[i]]를 사용하는가?
"현재 아이템을 넣으려면, 그 공간을 비워야 한다"
예시: 용량 5칸에 신검(3칸)을 넣으려면
→ 3칸을 비우고, 남은 2칸으로 최선을 다해야 함
→ 하지만! 신검은 아직 안 본 상태에서 2칸의 최선을 구해야 함
→ 따라서 dp[i-1][2] (신검 보기 "전"의 2칸 최대 가치)
만약 dp[i][2]를 썼다면?
→ 신검을 이미 고려한 상태 (순환 참조!)
→ 신검을 2번 넣는 오류 발생 가능
i-1을 쓰는 이유: "아직 현재 아이템을 고려하지 않은 세계"의 값을 가져오기 위해!
Plain Text
복사
경계 조건
if (weight[i] > w)
{
dp[i][w] = dp[i-1][w]; // 용량 초과 시 선택 불가
}
C++
복사
예시: 용량 2칸인데 신검(3칸)을 고려하는 경우
물리적으로 불가능! → 선택지가 1개뿐
→ dp[2][2] = dp[1][2] (신검을 넣지 않은 경우만 가능)
Plain Text
복사
 단계별 DP 테이블 구성
단계별 DP 테이블 구성
아이템 정보 정리
아이템 1: 💍 마법반지 (2칸, 가치 3)
아이템 2: ⚔️ 신검 (3칸, 가치 4)
아이템 3: 🛡️ 용방패 (4칸, 가치 5)
아이템 4: 👑 왕의왕관 (5칸, 가치 6)
Plain Text
복사
초기화
용량 → 0 1 2 3 4 5
아이템 ↓
0개 (없음) 0 0 0 0 0 0
Plain Text
복사
1단계: 마법반지 (2칸, 가치 3) 추가
💭 각 용량별 계산:
- 용량 0~1: 마법반지(2칸)이 안들어감 → 0
- 용량 2~5: 마법반지 들어감 → 가치 3
용량 → 0 1 2 3 4 5
아이템 ↓
0개 (없음) 0 0 0 0 0 0
1개 (반지) 0 0 3 3 3 3
Plain Text
복사
2단계: 신검 (3칸, 가치 4) 추가
💭 핵심 계산 (용량 5):
dp[2][5] = max
(
dp[1][5], // 신검 안가져가기 = 3
dp[1][5-3] + 4 // 신검 가져가기 = dp[1][2] + 4 = 3 + 4 = 7
)
→ max(3, 7) = 7 선택! (반지 + 신검)
용량 → 0 1 2 3 4 5
아이템 ↓
0개 (없음) 0 0 0 0 0 0
1개 (반지) 0 0 3 3 3 3
2개 (신검) 0 0 3 4 4 7
Plain Text
복사
3단계: 용방패 (4칸, 가치 5) 추가
💭 핵심 계산 (용량 5):
dp[3][5] = max(
dp[2][5], // 용방패 안가져가기 = 7
dp[2][5-4] + 5 // 용방패 가져가기 = dp[2][1] + 5 = 0 + 5 = 5
)
→ max(7, 5) = 7 선택! (반지 + 신검이 더 좋음)
용량 → 0 1 2 3 4 5
아이템 ↓
0개 (없음) 0 0 0 0 0 0
1개 (반지) 0 0 3 3 3 3
2개 (신검) 0 0 3 4 4 7
3개 (용방패) 0 0 3 4 5 7
Plain Text
복사
4단계: 왕의왕관 (5칸, 가치 6) 추가
💭 핵심 계산 (용량 5):
dp[4][5] = max(
dp[3][5], // 왕관 안가져가기 = 7
dp[3][5-5] + 6 // 왕관 가져가기 = dp[3][0] + 6 = 0 + 6 = 6
)
→ max(7, 6) = 7 선택! (반지 + 신검 조합이 최고)
용량 → 0 1 2 3 4 5
아이템 ↓
0개 (없음) 0 0 0 0 0 0
1개 (반지) 0 0 3 3 3 3
2개 (신검) 0 0 3 4 4 7
3개 (용방패) 0 0 3 4 5 7
4개 (왕관) 0 0 3 4 5 7 ← 최종!
Plain Text
복사
 완전한 C++ 구현
완전한 C++ 구현
#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
using namespace std;
int main()
{
// 게임 설정
int capacity = 5;
vector<string> items = { "💍마법반지", "⚔️신검", "🛡️용방패", "👑왕의왕관" };
vector<int> weights = { 2, 3, 4, 5 };
vector<int> values = { 3, 4, 5, 6 };
int n = items.size();
// DP 테이블 초기화
vector<vector<int>> dp(n + 1, vector<int>(capacity + 1, 0));
cout << "🎮 RPG 게임 - 던전 아이템 수집하기" << endl;
cout << "🎒 인벤토리 용량: " << capacity << "칸\n" << endl;
// 아이템 정보 출력
cout << "💎 발견한 아이템들:" << endl;
for (int i = 0; i < n; i++)
{
cout << " " << (i + 1) << ". " << items[i]
<< " (용량: " << weights[i] << "칸, 가치: " << values[i] << ")" << endl;
}
cout << endl;
// DP 계산
for (int i = 1; i <= n; i++)
{
cout << "📋 " << i << "단계: " << items[i - 1] << " 검토 중..." << endl;
for (int w = 0; w <= capacity; w++)
{
if (weights[i - 1] > w)
{
// 현재 아이템이 용량을 초과하는 경우
dp[i][w] = dp[i - 1][w];
}
else
{
// 선택하지 않는 경우와 선택하는 경우 중 최대값
int not_take = dp[i - 1][w];
int take = dp[i - 1][w - weights[i - 1]] + values[i - 1];
dp[i][w] = max(not_take, take);
// 최대 용량에서의 계산 과정 출력
if (w == capacity)
{
cout << " 용량 " << w << "칸: max(" << not_take
<< ", " << take << ") = " << dp[i][w] << endl;
}
}
}
cout << endl;
}
// 최종 DP 테이블 출력
cout << "📊 최종 DP 테이블:" << endl;
cout << " ";
for (int w = 0; w <= capacity; w++)
{
cout << "c" << w << " ";
}
cout << endl;
for (int i = 0; i <= n; i++)
{
if (i == 0)
{
cout << "없음: ";
}
else
{
cout << i << "개: ";
}
for (int w = 0; w <= capacity; w++)
{
cout << dp[i][w] << " ";
}
cout << endl;
}
cout << "\n🏆 최대 가치: " << dp[n][capacity] << endl;
// 선택된 아이템 역추적
cout << "\n🎒 선택된 아이템들:" << endl;
vector<bool> selected(n, false);
int w = capacity;
for (int i = n; i > 0 && w > 0; i--)
{
if (dp[i][w] != dp[i - 1][w])
{
selected[i - 1] = true;
cout << " ✅ " << items[i - 1]
<< " (용량: " << weights[i - 1] << "칸, 가치: " << values[i - 1] << ")" << endl;
w -= weights[i - 1];
}
else
{
cout << " ❌ " << items[i - 1] << " (선택하지 않음)" << endl;
}
}
// 최종 요약
int total_weight = 0, total_value = 0;
for (int i = 0; i < n; i++)
{
if (selected[i])
{
total_weight += weights[i];
total_value += values[i];
}
}
cout << "\n📋 최종 요약:" << endl;
cout << " 총 사용 용량: " << total_weight << "/" << capacity << "칸" << endl;
cout << " 총 가치: " << total_value << endl;
cout << " 남은 용량: " << (capacity - total_weight) << "칸" << endl;
return 0;
}
C++
복사
 결과 분석 및 역추적
결과 분석 및 역추적
최적해: 가치 7
🎒 선택된 아이템 조합:
✅ 💍 마법반지 (2칸, 가치 3)
✅ ⚔️ 신검 (3칸, 가치 4)
❌ 🛡️ 용방패 (선택하지 않음)
❌ 👑 왕의왕관 (선택하지 않음)
총 사용 용량: 2 + 3 = 5칸 (꽉 참!)
총 가치: 3 + 4 = 7
Plain Text
복사
역추적 과정
1. dp[4][5] = 7, dp[3][5] = 7 → 왕관 선택 안함 ❌
2. dp[3][5] = 7, dp[2][5] = 7 → 용방패 선택 안함 ❌
3. dp[2][5] = 7, dp[1][5] = 3 → 신검 선택! ✅ (남은 용량: 5-3=2)
4. dp[1][2] = 3, dp[0][2] = 0 → 마법반지 선택! ✅
Plain Text
복사
왜 이 조합이 최적일까?
다른 가능한 조합들:
- 👑 왕관만: 5칸, 가치 6
- 🛡️ 용방패만: 4칸, 가치 5
- 💍 반지 + ⚔️ 신검: 5칸, 가치 7 ← 최고!
작은 아이템들의 조합이 큰 아이템 하나보다 더 효율적!
Plain Text
복사
 핵심 개념 정리
핵심 개념 정리
1. DP의 핵심 아이디어
•
최적 부분 구조: 작은 문제의 최적해로 큰 문제의 최적해 구성
•
중복 부분 문제: 같은 계산을 여러 번 하지 않도록 결과 저장
•
점진적 구성: 아이템을 하나씩 추가하며 최적해 갱신
2. 선택의 기준
각 단계에서 두 가지 선택:
1. 현재 아이템 선택 안함 → 이전 상태 그대로
2. 현재 아이템 선택함 → 남은 공간의 최적해 + 현재 아이템 가치
Plain Text
복사
3. 시간/공간 복잡도
•
시간 복잡도: O(n × W) = O(4 × 5) = O(20)
•
공간 복잡도: O(n × W) = O(20)
4. 실전 팁
•
작은 아이템 조합 vs 큰 아이템: 효율성 비교 중요
•
역추적: 최적해가 어떤 선택들로 구성되었는지 파악
•
경계 조건: 용량 초과 시 처리 주의
 세 가지 DP 문제 비교
세 가지 DP 문제 비교
구분 | 동전 문제 | 피보나치 | 배낭 문제 |
DP 차원 | 1차원 | 1차원 | 2차원 |
상태 정의 | dp[i] = i원을 만드는 경우의 수 | dp[i] = i번째 피보나치 수 | dp[i][w] = i개 물건, 용량w에서 최대 가치 |
점화식 | dp[i] += dp[i-coin] | dp[i] = dp[i-1] + dp[i-2] | dp[i][w] = max(dp[i-1][w], dp[i-1][w-weight] + value) |
시간복잡도 | O(amount × coins) | O(n) | O(n × W) |
공간복잡도 | O(amount) | O(n) | O(n × W) |
 DP 마스터 체크리스트
DP 마스터 체크리스트
 문제 분석 단계
문제 분석 단계
1.
중복 부분 문제가 있는가?
•
같은 하위 문제가 여러 번 계산되는지 확인
2.
최적 부분 구조를 만족하는가?
•
작은 문제의 최적해가 큰 문제의 최적해에 포함되는지 확인
3.
무후효성을 만족하는가?
•
현재 상태가 과거 경로와 무관하게 결정되는지 확인
 구현 전략
구현 전략
1.
Top-down (재귀 + 메모이제이션)
int dp[MAX];
int solve(int n)
{
if (dp[n] != -1) return dp[n]; // 이미 계산됨
return dp[n] = /* 점화식 */;
}
C++
복사
2.
Bottom-up (반복문)
vector<int> dp(n + 1);
dp[0] = /* 초기값 */;
for (int i = 1; i <= n; i++)
{
dp[i] = /* 점화식 */;
}
C++
복사
 최적화 기법
최적화 기법
1.
공간 최적화: 필요한 이전 상태만 저장
2.
상태 압축: 2차원을 1차원으로 변환
3.
계산 순서 최적화: 불필요한 계산 생략
 실전 DP 문제 해결 전략
실전 DP 문제 해결 전략
 문제 접근 순서
문제 접근 순서
1.
브루트포스 솔루션 먼저 생각
•
모든 경우를 다 해보는 재귀 함수 작성
•
시간복잡도가 너무 크다면 DP 고려
2.
상태와 점화식 정의
•
dp[i]가 무엇을 나타내는지 명확히 정의
•
상태 간의 관계식 도출
3.
기저 조건 설정
•
가장 작은 문제의 답을 직접 설정
•
경계 조건 처리
4.
계산 순서 결정
•
의존성을 고려한 계산 순서
•
Bottom-up vs Top-down 선택
 디버깅 팁
디버깅 팁
1.
작은 케이스로 손 계산: 점화식이 맞는지 검증
2.
DP 테이블 출력: 중간 과정 확인
3.
경계 조건 체크: 배열 범위 초과 방지
4.
초기값 확인: 기저 조건이 올바른지 검토
 핵심 정리
핵심 정리
1.
DP = 과거의 최적해 + 현재 선택 = 새로운 최적해
2.
테이블 크기: 보통 문제 범위 + 1
3.
점화식이 핵심: 상태 간의 관계를 정확히 파악
4.
초기값 중요: 기저 조건을 올바르게 설정
 현실적인 DP 학습 과정:
현실적인 DP 학습 과정:
 초보자의 전형적인 시행착오:
초보자의 전형적인 시행착오:
문제를 본다 → "어... 뭔가 복잡하네?"
→ 그리디로 시도 → 반례 발견 😱
→ 브루트포스로 시도 → 시간초과 😵
→ "이게 뭔 문제지?" → 답 확인 → "아, DP구나..."
Plain Text
복사
 점진적 감각 발달:
점진적 감각 발달:
5-10문제 후: "어? 이거 아까 본 패턴 같은데?"
20-30문제 후: "이런 키워드 나오면 DP일 확률 높아"
50문제 후: "문제 읽자마자 DP 냄새가 난다"
100문제 후: "이건 1차원 DP, 저건 2차원 DP"
Plain Text
복사
 실제 도움되는 학습법:
실제 도움되는 학습법:
 의도적으로 실패해보기
의도적으로 실패해보기
// 1. 일부러 재귀로 먼저 풀어보기
int slowFib(int n)
{
if (n <= 1) return n;
return slowFib(n-1) + slowFib(n-2);
}
// 2. "어? 너무 느리네" 경험하기
// 3. 같은 계산 반복 발견하기
// 4. "아하! 이걸 저장하면 되겠다" 깨달음
C++
복사
 문제 유형별 외우기
문제 유형별 외우기
그냥 외워버리는 것도 방법:
- "경우의 수" → DP 의심
- "최소 개수" → DP 의심
- "배낭, 동전, 계단" → 무조건 DP
- "피보나치 같은 점화식" → DP
Plain Text
복사
정말 솔직히 말하면, 처음 20-30문제는 답 보고 "아, 이런 게 DP구나" 하면서 패턴을 익히는 게 가장 효율적입니다!
무작정 고민하다가 시간만 낭비하는 것보다는, 답을 보고 "왜 DP인지" 이해하는 게 더 도움이 돼요. 

“강의는 많은데, 왜 나는 아직도 코드를 못 짤까?”
혼자 공부하다 보면 누구나 이런 고민을 하게 됩니다.
•
강의는 다 들었지만 막상 손이 안 움직이고,
•
복습을 하려 해도 무엇을 다시 봐야 할지 모르겠고,
•
질문할 곳도 없고,
•
유튜브는 결국 정답을 따라 치는 것밖에 안 되는 것 같고.
문제는 ‘연습’이 빠졌기 때문입니다.
단순히 강의를 듣는 것만으로는 실력이 늘지 않습니다.
실제 문제를 풀고, 고민하고, 직접 구현해보는 시간이 반드시 필요합니다.
그래서, 얌얌코딩 코칭은 다릅니다.
그냥 가르치지 않습니다.
스스로 설계하고, 코딩할 수 있게 만듭니다.
얌얌코딩 코칭에서는 단순한 예제가 아닌,
스스로 문제를 분석하고 구현해야 하는 연습문제를 제공합니다.
이 연습문제들은 다음과 같은 역량을 키우기 위해 설계되어 있습니다:
•
문제를 스스로 쪼개고 설계하는 힘
•
다양한 조건을 만족시키는 실제 구현 능력
•
기능 단위가 아닌, 프로그램 단위로 사고하는 습관
•
마침내 자신의 힘으로 코드를 끝까지 작성하는 경험
지금 필요한 건 더 많은 강의가 아닙니다.
코드를 스스로 완성해 나가는 훈련,
그것이 지금 실력을 끌어올릴 가장 현실적인 방법입니다.