계수정렬 (Counting Sort) & 해시테이블 (Hash Table)
계수정렬 (Counting Sort)
핵심 개념
Counting sort는 정렬 알고리즘중 하나로, 키 값의 범위가 제한된 정수 일때 매우 효율적인 방법. 다른 비교기반 정렬 알고리즘과 달리, 비교를 하지 않고 숫자의 발생 횟수를 카운트하여 정렬을 수행한다.
시간 복잡도가 O(n+k)이다. 데이터크기와 데이터 값의 범위에 비례한다.
카운팅소트의 동작원리
1. 입력데이터와 범위를 미리 알아두어야 한다. 예를 들어 0에서 100사이의 정수만을 다룬다면, 해당범위에 맞춰 알고리즘 동작
2. 각 데이터가 몇번씩 등장했는지 기록하는 카운트 배열을 만든다.
3. 카운트 배열을 통해 해당 숫자보다 작은 숫자가 몇개 있는지 계산한다.
4. 원래 배열의 숫자를 하나씩 꺼내면서 정렬된 위치에 배치한다.
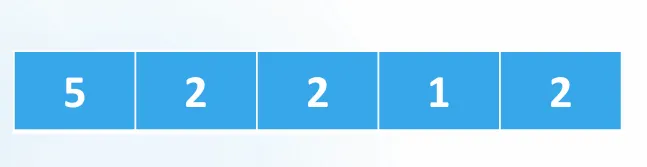
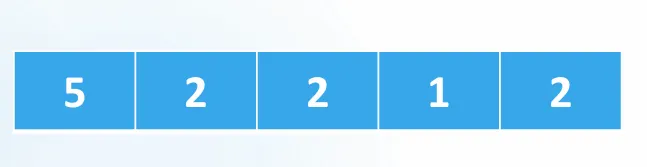
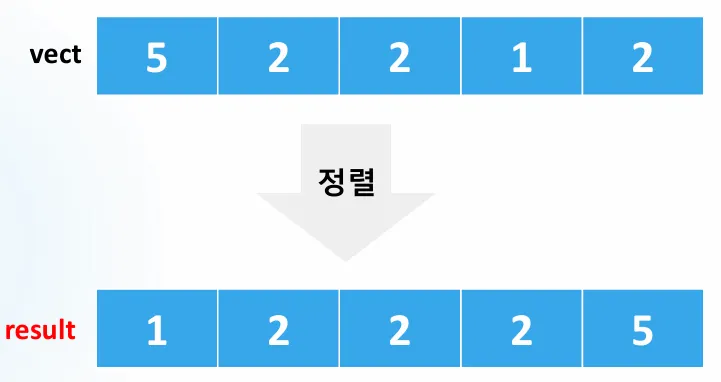
예제: [5, 2, 2, 1, 2] 정렬
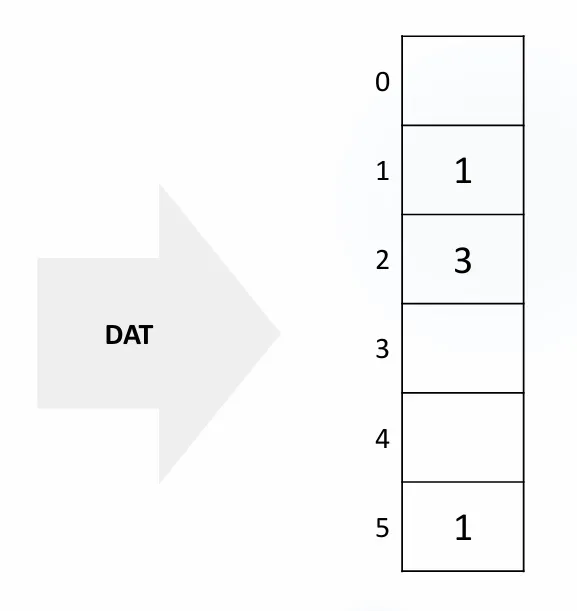
1단계: 정렬할 값들을 count 배열에 저장한다.
원본 배열: [5, 2, 2, 1, 2]
카운트 배열 구성:
숫자 | 0 | 1 | 2 | 3 | 4 | 5 |
개수 | 0 | 1 | 3 | 0 | 0 | 1 |
각 숫자의 등장 횟수를 센다:
- 1이 1번 등장
- 2가 3번 등장
- 5가 1번 등장
Plain Text
복사
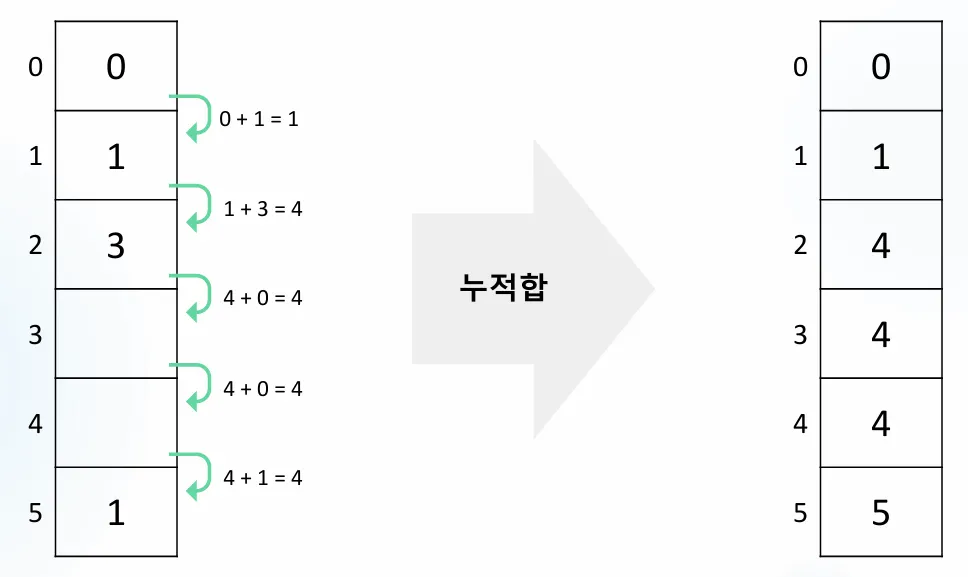
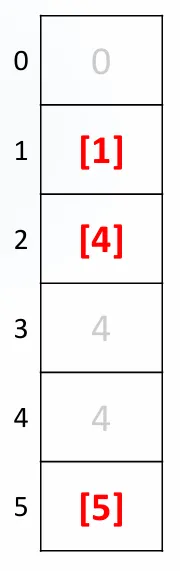
2단계: 누적합을 구해준다.
누적합 계산 과정:
index 0: 0
index 1: 0 + 1 = 1
index 2: 1 + 3 = 4
index 3: 4 + 0 = 4
index 4: 4 + 0 = 4
index 5: 4 + 1 = 5
결과 배열: [0, 1, 4, 4, 4, 5]
Plain Text
복사
누적합을 구하는 이유
신기하게도 정렬할 값들이 result 배열에 들어 갈 수 있는 LastIndex가 결정된다.
예시 분석:
- 숫자 5는 result[5-1]에 들어가면 된다.
- 숫자 2는 result[4-1]에 들어가면 된다.
- 숫자 1은 result[1-1]에 들어가면 된다.
(index에 -1을 해주면 result[0]부터 채울 수 있다.)
최종 결과: [1, 2, 2, 2, 5]
Plain Text
복사
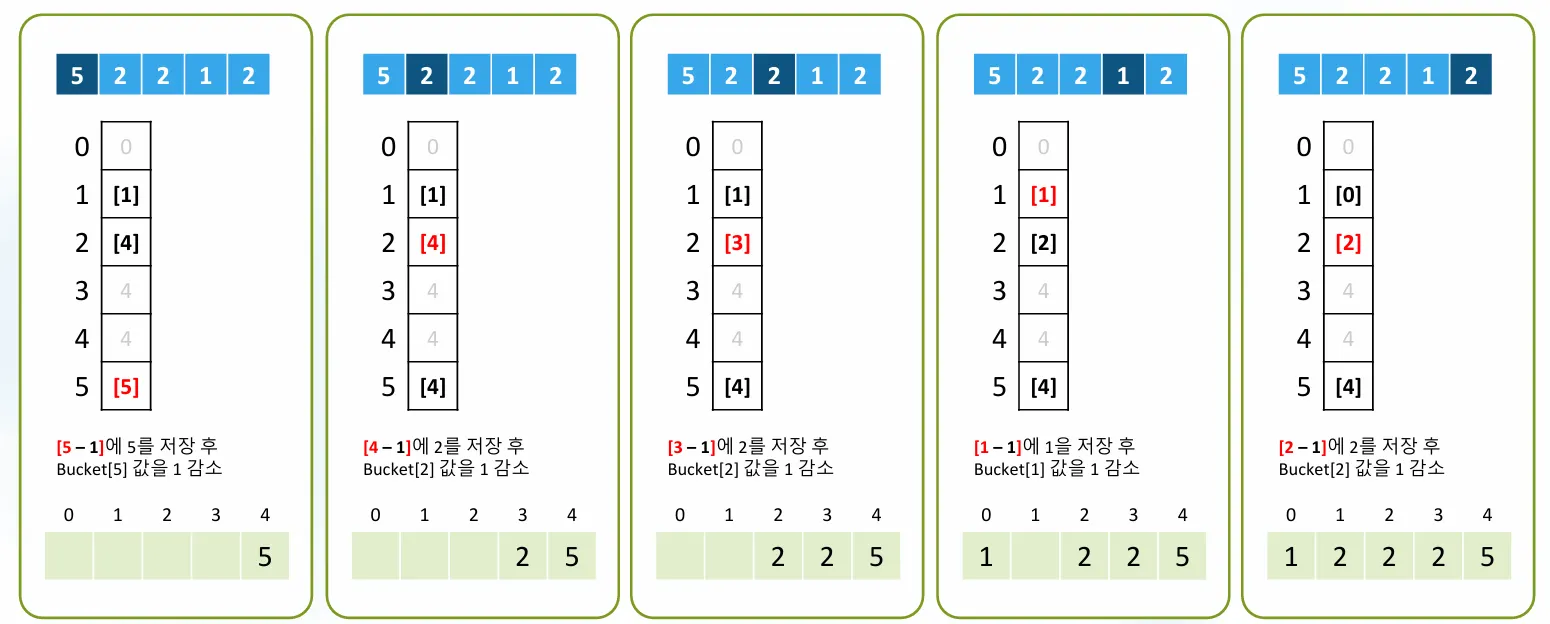
3단계: 누적합을 이용하여 정렬 결과 저장
원본 배열을 뒤에서부터 처리하여 안정 정렬 보장:
3단계 과정 (5단계별 세부 처리):
1. 숫자 2 처리: count[2]=4 → result[3]=2, count[2]=3
2. 숫자 1 처리: count[1]=1 → result[0]=1, count[1]=0
3. 숫자 2 처리: count[2]=3 → result[2]=2, count[2]=2
4. 숫자 2 처리: count[2]=2 → result[1]=2, count[2]=1
5. 숫자 5 처리: count[5]=5 → result[4]=5, count[5]=4
정렬된 값을 하나씩 담색하면서, 제 위치에다가 값을 저장한다.
Plain Text
복사
계수정렬 완전 구현
#include <iostream>
#include <queue>
int main()
{
int arr[5] = { 5, 2, 2, 1, 2 };
int bucket[6] = { }; // 카운트 배열
int result[5] = { }; // 결과 배열
//1. bucket에 arr의 값을 넣어준다.
for (size_t i = 0; i < 5; i++)
{
bucket[arr[i]]++;
}
//2. bucket의 값을 누적시킨다.
for (size_t i = 1; i < 6; i++)
{
bucket[i] += bucket[i - 1];
}
//3. result에 bucket의 값을 넣어준다.
for (size_t i = 0; i < 5; i++)
{
int index = bucket[arr[i]] - 1;
result[index] = arr[i];
bucket[arr[i]]--; // 같은 값의 다음 위치를 위해 감소
}
// 결과 출력
std::cout << "정렬 결과: ";
for (int i = 0; i < 5; i++)
{
std::cout << result[i] << " ";
}
std::cout << std::endl;
return 0;
}
C++
복사
계수정렬의 특징
장점
1.
매우 빠른 속도: O(n+k) 시간복잡도
2.
안정 정렬: 같은 값의 상대적 순서 유지
3.
비교 없음: 값의 비교 연산 불필요
단점
1.
범위 제한: 정수만 가능, 범위가 클 수록 비효율
2.
추가 메모리: O(k) 공간 필요 (k = 값의 범위)
3.
범위 의존적: 값의 범위가 크면 사용 불가
사용 적합한 경우
•
정수 데이터
•
값의 범위가 작을 때 (보통 n과 비슷하거나 작을 때)
•
안정 정렬이 필요한 경우
•
최고 성능이 필요한 경우
해시테이블 (Hash Table) - unordered_map
핵심 개념
C++에서 제공하는 해시테이블 기반의 컨테이너입니다. 이 컨테이너는 키값과 데이터값 쌍으로 이루어져있다.
키를 기준으로 인덱스에 접근하기 때문에 데이터를 검색, 삽입할때 빠른속도로 사용 할 수 있다.
해시테이블의 특징
1. 해시 기반: 내부적으로 해시함수를 사용해서 키를 계산하기 때문에, 평균 시간 복잡도가 삽입, 삭제, 검색 전부 O(1)이다.
2. 키의 순서 보장이 되지 않는다: 삽입되는 순서가 유지되지 않는다. 내부적으로 해시테이블에 저장되기때 문에, 순서가 무작위이다.
3. 중복되는 키값을 허용 않는다: 각 키는 고유해야 하며, 중복된 값을 사용하면 그냥 덮어 씌어진다
4. 시간복잡도는 O(1)이다: 그치만 해시 충돌이 많이질 경우 O(n)까지도 늘어날수도 있다.
unordered_map 기본 사용법
#include <iostream>
#include <unordered_map>
int main()
{
std::unordered_map<std::string, int> age_map;
// 삽입
age_map["Alice"] = 25;
//age_map.insert(std::make_pair("Bob", 30));
age_map["Bob"] = 30;
age_map["Charlie"] = 22;
// 값 접근
std::cout << "Alice's age: " << age_map["Alice"] << std::endl;
// 존재 여부 확인
if (age_map.find("Bob") != age_map.end())
{
std::cout << "Bob is in the map." << std::endl;
}
// 삭제
age_map.erase("Charlie");
// 전체 순회
for (const auto& pair : age_map)
{
std::cout << pair.first << ": " << pair.second << std::endl;
}
return 0;
}
C++
복사
주요 함수들
삽입 연산
// 방법 1: [] 연산자
map["key"] = value;
// 방법 2: insert 함수
map.insert(std::make_pair("key", value));
map.insert({"key", value}); // C++11 이후
C++
복사
조회 연산
// 방법 1: [] 연산자 (없으면 기본값으로 생성)
int value = map["key"];
// 방법 2: at() 함수 (없으면 예외 발생)
int value = map.at("key");
// 방법 3: find() 함수 (가장 안전)
auto it = map.find("key");
if (it != map.end())
{
int value = it->second;
}
C++
복사
삭제 연산
// 키로 삭제
map.erase("key");
// 반복자로 삭제
auto it = map.find("key");
if (it != map.end())
{
map.erase(it);
}
// 전체 삭제
map.clear();
C++
복사
기타 유용한 함수들
// 크기 확인
size_t size = map.size();
// 비어있는지 확인
bool empty = map.empty();
// 키 존재 여부 (C++20)
bool exists = map.contains("key");
// 개수 세기 (0 또는 1)
size_t count = map.count("key");
C++
복사
해시테이블 vs 다른 자료구조
구분 | unordered_map | map | vector |
평균 시간복잡도 | O(1) | O(log n) | O(n) |
최악 시간복잡도 | O(n) | O(log n) | O(n) |
순서 보장 | | (정렬됨) | (삽입순) |
메모리 사용 | 높음 | 보통 | 낮음 |
사용 적합성 | 빠른 검색 | 정렬된 데이터 | 순차 접근 |
실전 활용 예제
1. 문자 빈도 계산
std::unordered_map<char, int> charCount;
std::string text = "hello world";
for (char c : text)
{
charCount[c]++; // 없으면 0으로 초기화 후 증가
}
// 결과: h(1), e(1), l(3), o(2), ' '(1), w(1), r(1), d(1)
C++
복사
2. 두 수의 합 문제
std::vector<int> twoSum(std::vector<int>& nums, int target)
{
std::unordered_map<int, int> numMap;
for (int i = 0; i < nums.size(); i++)
{
int complement = target - nums[i];
if (numMap.find(complement) != numMap.end())
{
return {numMap[complement], i};
}
numMap[nums[i]] = i;
}
return {};
}
C++
복사
주의사항
해시 충돌
// 해시 충돌이 많이 발생하면 성능 저하
// 좋은 해시 함수를 사용하는 것이 중요
// 커스텀 해시 함수 예제
struct StringHash
{
size_t operator()(const std::string& s) const {
return std::hash<std::string>{}(s);
}
};
C++
복사
메모리 사용량
// 해시테이블은 추가 메모리를 많이 사용
// 로드 팩터(load factor)에 따라 메모리 사용량 결정
// 기본적으로 75% 로드 팩터에서 재해싱
C++
복사
핵심 정리
계수정렬
1.
O(n+k) 시간복잡도로 매우 빠름
2.
정수 범위가 제한적일 때만 사용 가능
3.
안정 정렬이며 비교 연산 불필요
4.
추가 메모리 O(k) 필요
해시테이블 (unordered_map)
1.
평균 O(1) 시간복잡도로 빠른 검색/삽입/삭제
2.
키의 순서 보장 안됨
3.
해시 충돌 시 성능 저하 가능
4.
빈도 계산, 캐시, 매핑 등에 유용
unordered_map은 순서를 신경 쓰지 않고 빨르게 키 기반으로 데이터를 조회하고자 할 때 매우 유용한 컨테이너입니다.
이 코드는 간단한 캐시(Cache) 클래스입니다!
SimpleCache 클래스 상세 분석
캐시란?
자주 사용하는 데이터를 빠르게 접근할 수 있도록 임시 저장하는 공간
예시:
- 웹사이트 방문 기록 저장
- 계산 결과 임시 보관
- 사용자 정보 빠른 조회
Plain Text
복사
클래스 구조 분석
1. Private 멤버
std::unordered_map<std::string, int> cache;
C++
복사
•
키: std::string (예: 사용자 이름, ID 등)
•
값: int (예: 나이, 점수, 카운트 등)
•
해시테이블 사용 → 빠른 O(1) 접근 속도
2. Public 함수들
put() 함수 - 데이터 저장
void put(const std::string& key, int value)
{
cache[key] = value;
}
C++
복사
•
역할: 키-값 쌍을 캐시에 저장
•
동작: cache["이름"] = 25 형태로 저장
•
특징: 같은 키가 있으면 값을 덮어씀
get() 함수 - 데이터 조회
int get(const std::string& key)
{
auto it = cache.find(key);
return (it != cache.end()) ? it->second : -1;
}
C++
복사
•
역할: 키에 해당하는 값 반환
•
안전한 조회: 키가 없으면 -1 반환 (크래시 방지)
•
삼항 연산자: 조건 ? 참일때값 : 거짓일때값
exists() 함수 - 존재 여부 확인
bool exists(const std::string& key)
{
return cache.find(key) != cache.end();
}
C++
복사
•
역할: 키가 캐시에 있는지 확인
•
반환: true(있음) 또는 false(없음)
실사용 예제
#include <iostream>
#include <unordered_map>
#include <string>
class SimpleCache
{
private:
std::unordered_map<std::string, int> cache;
public:
void put(const std::string& key, int value)
{
cache[key] = value;
std::cout << "저장: " << key << " = " << value << std::endl;
}
int get(const std::string& key)
{
auto it = cache.find(key);
if (it != cache.end()) {
std::cout << "조회 성공: " << key << " = " << it->second << std::endl;
return it->second;
} else {
std::cout << "조회 실패: " << key << " (없음)" << std::endl;
return -1;
}
}
bool exists(const std::string& key)
{
return cache.find(key) != cache.end();
}
void showAll()
{
std::cout << "\n=== 전체 캐시 내용 ===" << std::endl;
for (const auto& pair : cache) {
std::cout << pair.first << ": " << pair.second << std::endl;
}
}
};
int main()
{
SimpleCache myCache;
// 데이터 저장
myCache.put("Alice", 25);
myCache.put("Bob", 30);
myCache.put("Charlie", 22);
// 데이터 조회
int age = myCache.get("Alice"); // 25 반환
int unknown = myCache.get("David"); // -1 반환 (없음)
// 존재 여부 확인
if (myCache.exists("Bob"))
{
std::cout << "Bob이 캐시에 있습니다!" << std::endl;
}
if (!myCache.exists("Eve"))
{
std::cout << "Eve는 캐시에 없습니다." << std::endl;
}
// 전체 내용 출력
myCache.showAll();
return 0;
}
C++
복사
실행 결과
저장: Alice = 25
저장: Bob = 30
저장: Charlie = 22
조회 성공: Alice = 25
조회 실패: David (없음)
Bob이 캐시에 있습니다!
Eve는 캐시에 없습니다.
=== 전체 캐시 내용 ===
Alice: 25
Bob: 30
Charlie: 22
Plain Text
복사
핵심 포인트
1. 안전한 조회
// ❌ 위험한 방법 (키가 없으면 0으로 생성됨)
int value = cache["nonexistent"];
// ✅ 안전한 방법 (키가 없으면 -1 반환)
int value = get("nonexistent");
C++
복사
2. find() 함수의 작동 원리
auto it = cache.find("Alice");
if (it != cache.end()) {
// 찾았음! it->second가 값
std::cout << it->first << ": " << it->second << std::endl;
} else {
// 못찾음!
std::cout << "키가 없습니다." << std::endl;
}
C++
복사
3. 왜 -1을 반환하나?
•
0은 유효한 값일 수 있음 (나이가 0살인 경우)
•
1은 일반적으로 "없음"을 나타내는 관례
•
더 좋은 방법: std::optional<int> 사용 (C++17 이후)
개선된 버전
#include <optional> // C++17
class BetterCache {
private:
std::unordered_map<std::string, int> cache;
public:
void put(const std::string& key, int value)
{
cache[key] = value;
}
// optional을 사용한 더 안전한 get
std::optional<int> get(const std::string& key) {
auto it = cache.find(key);
if (it != cache.end()) {
return it->second; // 값이 있으면 반환
}
return std::nullopt; // 없으면 nullopt 반환
}
bool exists(const std::string& key) {
return cache.find(key) != cache.end();
}
};
// 사용법
BetterCache cache;
cache.put("Alice", 25);
auto result = cache.get("Alice");
if (result.has_value()) {
std::cout << "Alice의 나이: " << result.value() << std::endl;
} else {
std::cout << "Alice를 찾을 수 없습니다." << std::endl;
}
C++
복사
실전 활용 사례
1. 웹서버 세션 관리
SimpleCache sessionCache;
sessionCache.put("user123", 1); // 로그인됨
sessionCache.put("user456", 0); // 로그아웃됨
C++
복사
2. 계산 결과 캐싱
SimpleCache fibCache;
fibCache.put("fib_10", 55); // 피보나치(10) = 55 저장
fibCache.put("fib_15", 610); // 피보나치(15) = 610 저장
C++
복사
3. 게임 플레이어 점수
SimpleCache scoreCache;
scoreCache.put("player1", 1500);
scoreCache.put("player2", 2300);
C++
복사
요약
SimpleCache는:
•
해시테이블 기반의 빠른 캐시
•
put(): 저장, get(): 조회, exists(): 확인
•
O(1) 평균 성능으로 매우 빠름
•
간단하지만 실용적인 캐시 구현체
"자주 쓰는 데이터를 빠르게 꺼내 쓸 수 있는 임시 저장소" 라고 생각하면 됩니다!