퀵정렬 (Quick Sort)
기본 개념
퀵정렬은 분할정복 전략을 사용하는 정렬 알고리즘으로, 실무에서 가장 많이 사용되는 정렬 방법입니다.
핵심 아이디어:
1.
배열에서 피벗(pivot)이라는 기준값을 선택합니다.
2.
피벗을 기준으로 배열을 두 부분으로 분할합니다:
•
왼쪽 부분: 피벗보다 작은 값들
•
오른쪽 부분: 피벗보다 큰 값들
3.
분할된 두 부분에 대해 재귀적으로 퀵정렬을 수행합니다.
4.
더 이상 쪼갤 수 없을 때까지 반복하면 정렬이 완료됩니다.
퀵정렬 (Quick Sort) 상세 구현
 퀵정렬 특징
퀵정렬 특징
시간 복잡도에 따라서 o(nlogn)의 빠른 속도이지만, 데이터 값에 따라 O(n^2)나올 수 있다.
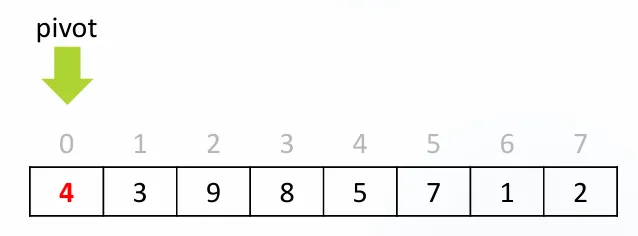
특정 범위에서 (start ~ end) 가장 왼쪽에 있는 숫자를 pivot으로 배치한다.
 퀵정렬 핵심 아이디어
퀵정렬 핵심 아이디어
1. 피벗(Pivot) 선택
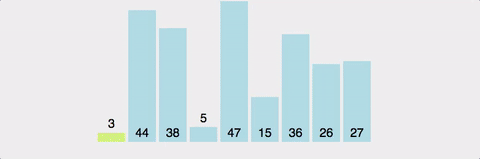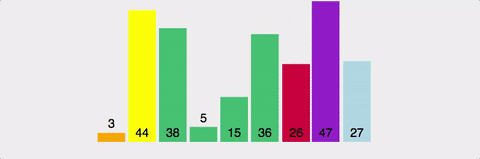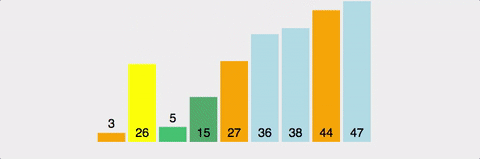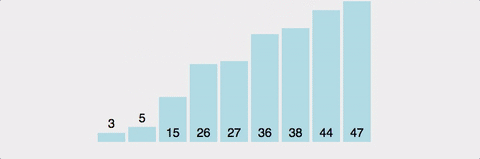
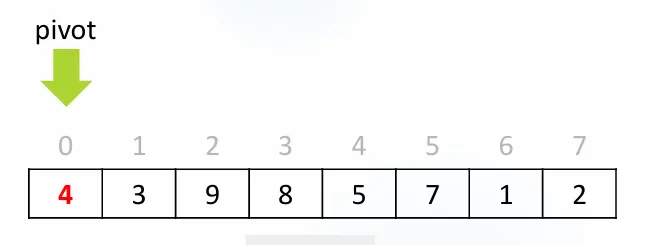
배열: [4, 3, 9, 8, 5, 7, 1, 2]
↑
pivot
특정 범위의 가장 왼쪽 원소를 피벗으로 선택
Plain Text
복사
2. 분할(Partition) 과정
여러번의 swap 작업을 통해 pivot의 위치를 결정하고,pivot 왼쪽에는 pivot보다 작은숫자를pivot 오른쪽에는 pivot보다 큰 숫자를 배치한다.
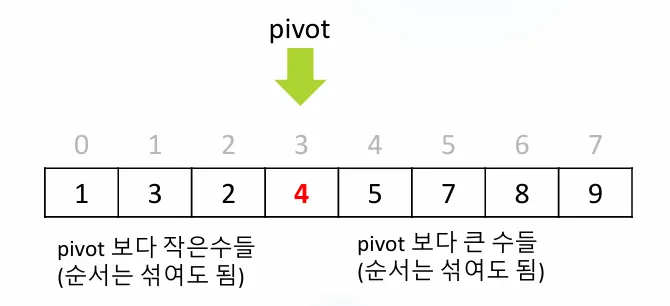
목표: pivot(4)를 기준으로 분할
- 왼쪽: 4보다 작은 수들 (순서는 섞여도 됨)
- 오른쪽: 4보다 큰 수들 (순서는 섞여도 됨)
Plain Text
복사
 분할 과정 상세 분석
분할 과정 상세 분석
이번에는 구간을 나누어서 같은 작업을 진행하면 된다.
초기 상태:
[4, 3, 9, 8, 5, 7, 1, 2]
Plain Text
복사
가장 작은 구간이 될때까지 재귀호출을 통해서 반복하여 위치를 실행해준다.
1단계: 두 부분으로 분할
원본: [1, 3, 2, 4, 5, 7, 8, 9]
←----- pivot보다 작은수들 pivot pivot보다 큰 수들 ----→
(순서는 섞여도 됨) (순서는 섞여도 됨)
Plain Text
복사
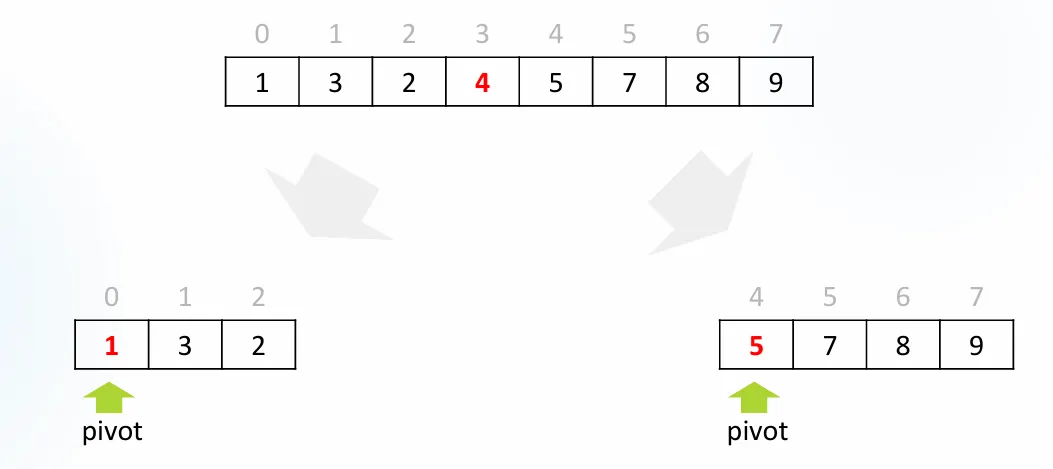
2단계: 각 부분을 재귀적으로 정렬
왼쪽 부분: [1, 3, 2] → pivot으로 다시 분할
오른쪽 부분: [5, 7, 8, 9] → pivot으로 다시 분할
Plain Text
복사
 세부과정: 투 포인터 분할 알고리즘
세부과정: 투 포인터 분할 알고리즘
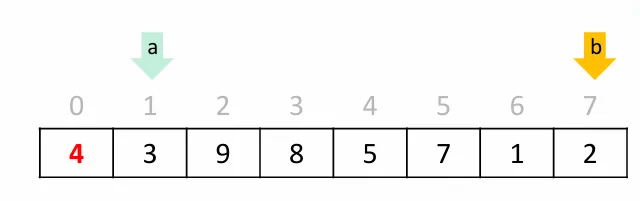
범수 a를 start + 1, 범수 b를 end로 설정해준다.
a++ 하면서 pivot보다 큰숫자를 찾는다. b-- 하면서 pivot보다 작은숫자를 찾는다.
1단계: a는 오른쪽으로, b는 왼쪽으로 이동
[4, 3, 9, 8, 5, 7, 1, 2]
↑ ↑
a(9>4 발견) b(2<4 발견)
Plain Text
복사
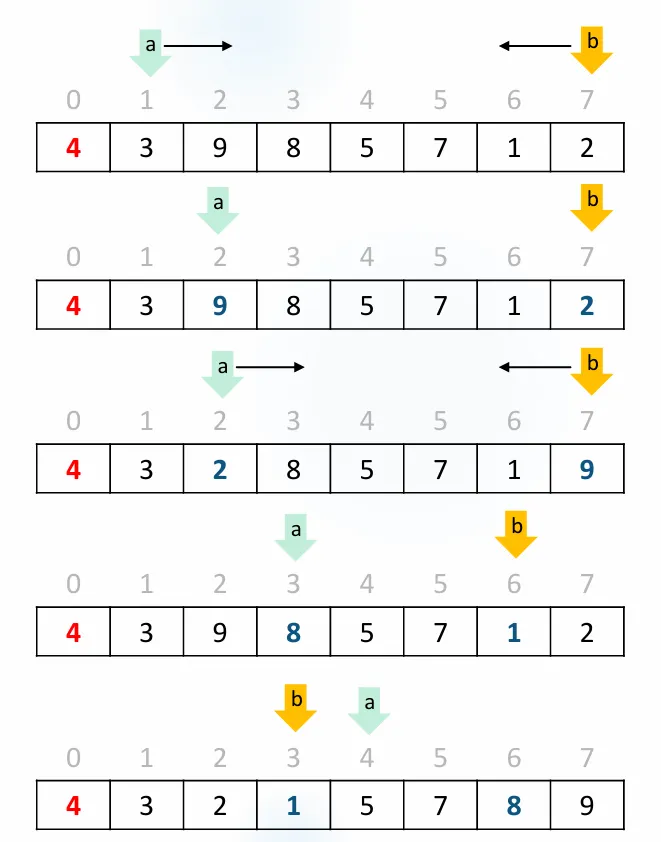
찾았으면 swap하여 바꿔주고, 이과정을 a와 b가 엇갈리기 전까지 반복해준다.
2단계: 9와 2를 교환
[4, 3, 2, 8, 5, 7, 1, 9]
↑ ↑
a b
3단계: 계속 진행
[4, 3, 2, 1, 5, 7, 8, 9]
↑ ↑
b a (엇갈림!)
Plain Text
복사
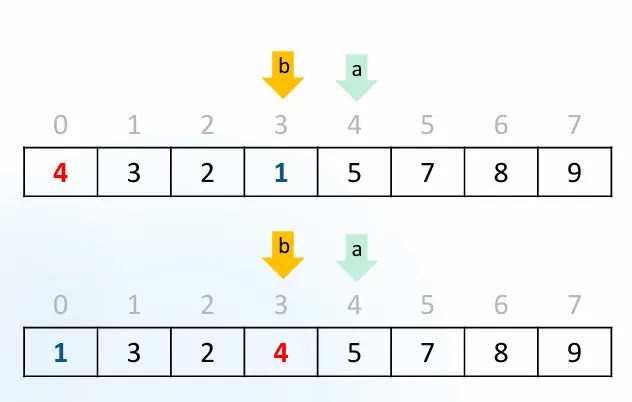
엇갈렸으면 마무리 단계로 pivot과 b를 swap하면 된다.
최종: pivot(4)과 b위치(1) 교환
[1, 3, 2, 4, 5, 7, 8, 9]
↑
pivot 최종 위치
Plain Text
복사
이제 pivot원쪽에는 전부 pivot보다 작은숫자들이 배치고, 오른쪽에는 큰 숫자들이 배치하게 된다.
 투 포인터 방식 구현 (방법 1)
투 포인터 방식 구현 (방법 1)
#include <iostream>
int vect[10] = { 4,3,9,8,5,7,1,2 };
int n = 8;
void quicksort(int start, int end)
{
if (start >= end)
return;
int pivot = start; // 첫 번째 원소를 피벗으로
int a = start + 1; // 왼쪽에서 시작
int b = end; // 오른쪽에서 시작
while (true)
{
// a: pivot보다 큰 원소를 찾을 때까지 오른쪽으로 이동
while (a <= end && vect[a] <= vect[pivot])
a++;
// b: pivot보다 작은 원소를 찾을 때까지 왼쪽으로 이동
while (b >= start && vect[b] > vect[pivot])
b--;
// a와 b가 엇갈렸으면 종료
if (a > b)
break;
// 찾은 원소들을 교환
std::swap(vect[a], vect[b]);
}
// pivot을 올바른 위치(b)로 이동
std::swap(vect[pivot], vect[b]);
// 재귀 호출로 좌우 부분 정렬
quicksort(start, b - 1); // 왼쪽 부분
quicksort(b + 1, end); // 오른쪽 부분
}
int main()
{
quicksort(0, n - 1);
// 결과 출력
for (int i = 0; i < n; i++) {
std::cout << vect[i] << " ";
}
return 0;
}
C++
복사
 Hoare 분할 방식 구현 (방법 2)
Hoare 분할 방식 구현 (방법 2)
#include <iostream>
int vect[10] = { 4,3,9,8,5,7,1,2 };
int n = 8;
void quicksort(int left, int right)
{
int i = left, j = right;
int pivot = vect[(left + right) / 2]; // 중간값을 피벗으로
/* partition */
while (i <= j)
{
// 왼쪽에서 피벗보다 큰 값 찾기
while (vect[i] < pivot)
i++;
// 오른쪽에서 피벗보다 작은 값 찾기
while (vect[j] > pivot)
j--;
// 교환 조건 만족시 교환
if (i <= j) {
std::swap(vect[i++], vect[j--]);
}
}
/* recursion */
if (left < j)
quicksort(left, j); // 왼쪽 부분 재귀
if (i < right)
quicksort(i, right); // 오른쪽 부분 재귀
}
int main()
{
quicksort(0, n - 1);
return 0;
}
C++
복사
 두 구현 방식 비교
두 구현 방식 비교
구분 | 방법 1 (Lomuto-style) | 방법 2 (Hoare-style) |
피벗 선택 | 첫 번째 원소 | 중간 원소 |
포인터 이동 | 한 방향씩 순차적 | 양방향 동시 |
교환 횟수 | 상대적으로 많음 | 상대적으로 적음 |
구현 난이도 | 이해하기 쉬움 | 약간 복잡 |
성능 | 보통 | 약간 더 빠름 |
 퀵정렬 동작 과정 시뮬레이션
퀵정렬 동작 과정 시뮬레이션
초기 배열: [4, 3, 9, 8, 5, 7, 1, 2]
1차 분할 후: [1, 3, 2, 4, 5, 7, 8, 9]
←--left--→ ↑ ←--right--→
pivot(4)
2차 분할:
왼쪽 [1, 3, 2]: pivot=1 → [1, 2, 3]
오른쪽 [5, 7, 8, 9]: 이미 정렬됨
3차 분할:
[2, 3]: pivot=2 → [2, 3]
최종 결과: [1, 2, 3, 4, 5, 7, 8, 9]
Plain Text
복사
 퀵정렬의 한계와 해결책
퀵정렬의 한계와 해결책
최악의 경우 O(n²)
이미 정렬된 배열: [1, 2, 3, 4, 5]
첫 번째 원소를 피벗으로 선택하면:
- 왼쪽: [] (빈 배열)
- 오른쪽: [2, 3, 4, 5] (거의 모든 원소)
이런 불균형 분할이 계속되면 O(n²)
Plain Text
복사
해결책들
1.
랜덤 피벗: 무작위로 피벗 선택
2.
중간값 피벗: 첫째, 중간, 마지막 중 중간값 선택
3.
Median-of-3: 세 값의 중간값을 피벗으로
4.
Intro Sort: 재귀 깊이가 깊어지면 힙정렬로 전환
 최적화된 퀵정렬
최적화된 퀵정렬
void optimizedQuickSort(int arr[], int low, int high) {
if (low < high) {
// 작은 배열은 삽입정렬 사용
if (high - low < 10) {
insertionSort(arr, low, high);
return;
}
// Median-of-3 피벗 선택
int mid = (low + high) / 2;
if (arr[mid] < arr[low]) swap(arr[mid], arr[low]);
if (arr[high] < arr[low]) swap(arr[high], arr[low]);
if (arr[high] < arr[mid]) swap(arr[high], arr[mid]);
int pi = partition(arr, low, high);
optimizedQuickSort(arr, low, pi - 1);
optimizedQuickSort(arr, pi + 1, high);
}
}
C++
복사
 핵심 포인트 정리
핵심 포인트 정리
분할(Partition)의 핵심
1.
피벗 선택: 보통 첫 번째, 마지막, 또는 중간 원소
2.
투 포인터: 양쪽에서 접근하여 교환할 원소 찾기
3.
교환: 조건에 맞는 원소들 위치 바꾸기
4.
피벗 배치: 최종적으로 피벗을 올바른 위치에 배치
재귀 호출
•
분할 완료 후: 피벗 기준으로 좌우 부분을 독립적으로 정렬
•
기저 조건: start >= end일 때 재귀 종료
•
점점 작은 문제: 전체 → 부분 → 더 작은 부분
시간복잡도
•
평균: O(nlogn) - 균등 분할
•
최악: O(n²) - 불균등 분할
•
공간: O(logn) - 재귀 스택
퀵정렬은 실제로 가장 많이 사용되는 정렬 알고리즘 중 하나입니다! 
“강의는 많은데, 왜 나는 아직도 코드를 못 짤까?”
혼자 공부하다 보면 누구나 이런 고민을 하게 됩니다.
•
강의는 다 들었지만 막상 손이 안 움직이고,
•
복습을 하려 해도 무엇을 다시 봐야 할지 모르겠고,
•
질문할 곳도 없고,
•
유튜브는 결국 정답을 따라 치는 것밖에 안 되는 것 같고.
문제는 ‘연습’이 빠졌기 때문입니다.
단순히 강의를 듣는 것만으로는 실력이 늘지 않습니다.
실제 문제를 풀고, 고민하고, 직접 구현해보는 시간이 반드시 필요합니다.
그래서, 얌얌코딩 코칭은 다릅니다.
그냥 가르치지 않습니다.
스스로 설계하고, 코딩할 수 있게 만듭니다.
얌얌코딩 코칭에서는 단순한 예제가 아닌,
스스로 문제를 분석하고 구현해야 하는 연습문제를 제공합니다.
이 연습문제들은 다음과 같은 역량을 키우기 위해 설계되어 있습니다:
•
문제를 스스로 쪼개고 설계하는 힘
•
다양한 조건을 만족시키는 실제 구현 능력
•
기능 단위가 아닌, 프로그램 단위로 사고하는 습관
•
마침내 자신의 힘으로 코드를 끝까지 작성하는 경험
지금 필요한 건 더 많은 강의가 아닙니다.
코드를 스스로 완성해 나가는 훈련,
그것이 지금 실력을 끌어올릴 가장 현실적인 방법입니다.