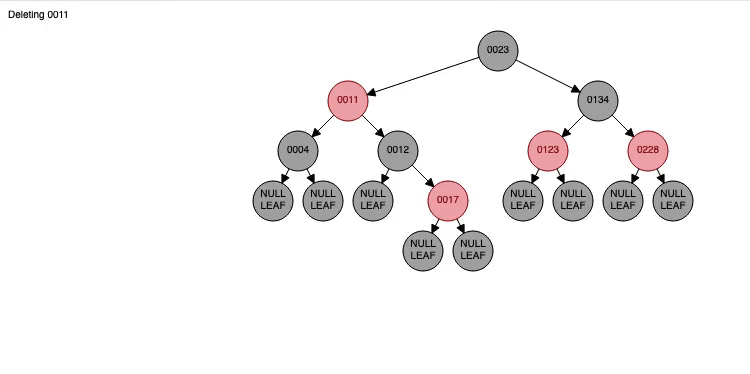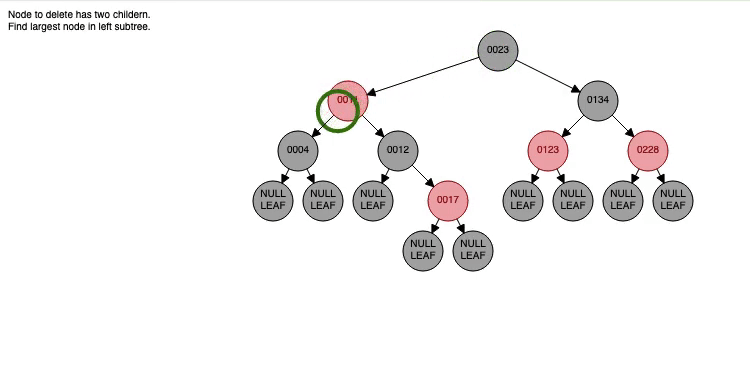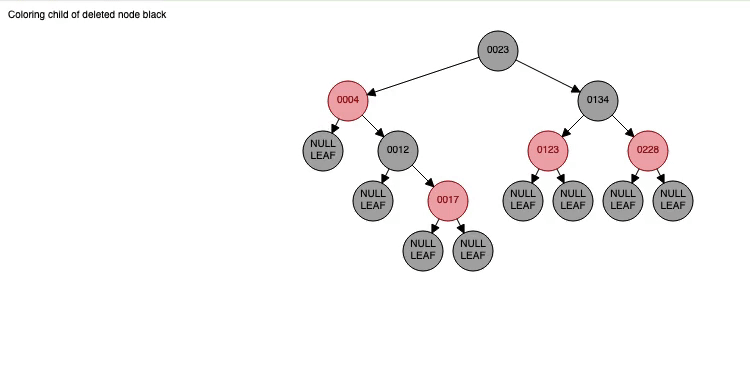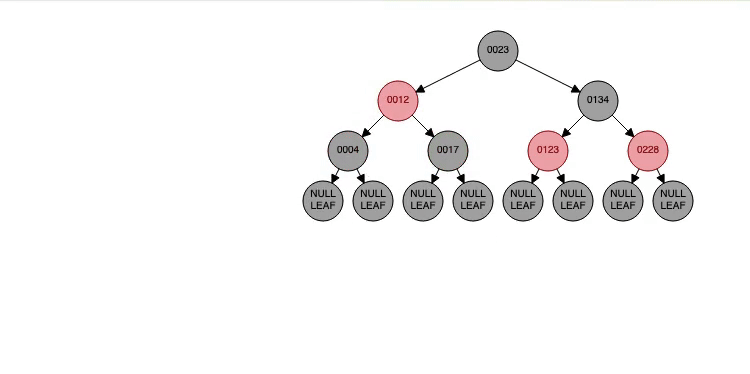
고급 트리정렬 & AVL 트리 (Advanced Tree Sort & AVL Tree)
트리정렬 재정의
이진 탐색 트리를 만들어서 정렬하는 방식이다. 추가될 값이 기존 노드보다 작으면 왼쪽으로, 모든값이 노드로 추가되어야 해당트리를 순회하는 방식으로 값을 정렬한다.
트리정렬의 핵심 과정
1. 데이터를 하나씩 이진 탐색 트리에 삽입
2. 중위 순회(In-order Traversal)로 정렬된 결과 출력
Plain Text
복사
기본 트리정렬의 한계
하지만 위와같은 방식은 모든 트리를 순회하는데 있어서 시간이 효율적일 수 있기 때문에 AVL(자가 균형 이진트리)를 이용하여 사용하는 경우가 많다.
문제 상황
최악의 경우 (이미 정렬된 입력):
1
\
2
\
3
\
4
\
5 → O(n²) 시간복잡도
Plain Text
복사
AVL 트리 (Adelson-Velsky and Landis Tree)
핵심 개념
자가 균형 이진 탐색 트리로, 모든 노드에서 왼쪽과 오른쪽 서브트리의 높이 차이가 최대 1을 넘지 않도록 유지한다.
AVL 트리의 균형 조건
Balance Factor (BF) = Height(Left Subtree) - Height(Right Subtree)
|BF| ≤ 1 (모든 노드에서)
Plain Text
복사
AVL 트리 예시
B
/ \
A D
/ \
C F
/ \
E G
모든 노드의 Balance Factor가 -1, 0, 1 중 하나
Plain Text
복사
AVL 트리의 회전 연산
1. LL 회전 (Left-Left Case)
z y
/ / \
y → x z
/ /
x T3
Plain Text
복사
2. RR 회전 (Right-Right Case)
x y
\ / \
y → x z
\ \
z T2
Plain Text
복사
3. LR 회전 (Left-Right Case)
z z x
/ / / \
y → x → y z
\ /
x y
Plain Text
복사
4. RL 회전 (Right-Left Case)
x x y
\ \ / \
z → y → x z
/ \
y z
Plain Text
복사
AVL 트리 기반 정렬 구현 개념
struct AVLNode
{
int data;
int height;
AVLNode* left;
AVLNode* right;
AVLNode(int value) : data(value), height(1), left(nullptr), right(nullptr) {}
};
class AVLTree
{
private:
AVLNode* root;
int getHeight(AVLNode* node)
{
return node ? node->height : 0;
}
int getBalanceFactor(AVLNode* node)
{
return node ? getHeight(node->left) - getHeight(node->right) : 0;
}
void updateHeight(AVLNode* node)
{
if (node)
node->height = 1 + std::max(getHeight(node->left), getHeight(node->right));
}
AVLNode* rotateRight(AVLNode* y)
{
AVLNode* x = y->left;
y->left = x->right;
x->right = y;
updateHeight(y);
updateHeight(x);
return x;
}
AVLNode* rotateLeft(AVLNode* x)
{
AVLNode* y = x->right;
x->right = y->left;
y->left = x;
updateHeight(x);
updateHeight(y);
return y;
}
AVLNode* insert(AVLNode* node, int value)
{
// 1. 일반적인 BST 삽입
if (!node) return new AVLNode(value);
if (value < node->data)
node->left = insert(node->left, value);
else
node->right = insert(node->right, value);
// 2. 높이 업데이트
updateHeight(node);
// 3. 균형 체크 및 회전
int balance = getBalanceFactor(node);
// LL Case
if (balance > 1 && value < node->left->data)
return rotateRight(node);
// RR Case
if (balance < -1 && value > node->right->data)
return rotateLeft(node);
// LR Case
if (balance > 1 && value > node->left->data)
{
node->left = rotateLeft(node->left);
return rotateRight(node);
}
// RL Case
if (balance < -1 && value < node->right->data)
{
node->right = rotateRight(node->right);
return rotateLeft(node);
}
return node;
}
public:
void insert(int value)
{
root = insert(root, value);
}
// 중위 순회로 정렬된 결과 출력
void inorderSort(std::vector<int>& result)
{
inorder(root, result);
}
void inorder(AVLNode* node, std::vector<int>& result)
{
if (node)
{
inorder(node->left, result);
result.push_back(node->data);
inorder(node->right, result);
}
}
};
C++
복사
성능 비교
구분 | 기본 BST | AVL 트리 | Red-Black 트리 |
삽입 시간복잡도 | O(n) ~ O(logn) | O(logn) | O(logn) |
탐색 시간복잡도 | O(n) ~ O(logn) | O(logn) | O(logn) |
균형 보장 | | | |
회전 횟수 | - | 많음 | 적음 |
구현 복잡도 | 낮음 | 높음 | 매우 높음 |
현대적 구현: STL 활용
가장 최근에는 std::map은 RED/BLACK 트리를 사용한다.
#include <map>
#include <set>
#include <vector>
void modernTreeSort(std::vector<int>& arr)
{
// Red-Black Tree 기반 (C++ STL)
std::multiset<int> balanced_tree;
// 1단계: 모든 원소를 균형 트리에 삽입 O(n log n)
for (int value : arr)
{
balanced_tree.insert(value);
}
// 2단계: 정렬된 순서로 다시 배열에 저장 O(n)
arr.assign(balanced_tree.begin(), balanced_tree.end());
}
C++
복사
AI 시대의 트리정렬
AI 기능을 사용하면 일력 후 스페이스 키를 누르세요. 명령어 사용 시에는 '/'를 누르세요...
AI가 도움을 줄 수 있는 영역
1.
최적의 트리 선택: 데이터 특성에 맞는 트리 구조 추천
2.
성능 분석: 입력 데이터 패턴 분석으로 성능 예측
3.
코드 최적화: 자동으로 균형 트리 구현 생성
4.
시각화: 트리 구조와 회전 과정 시각적 표현