MST 크루스칼 알고리즘 & BFS 길찾기 수업노트
MST: Minimum Spanning Tree
기본 개념
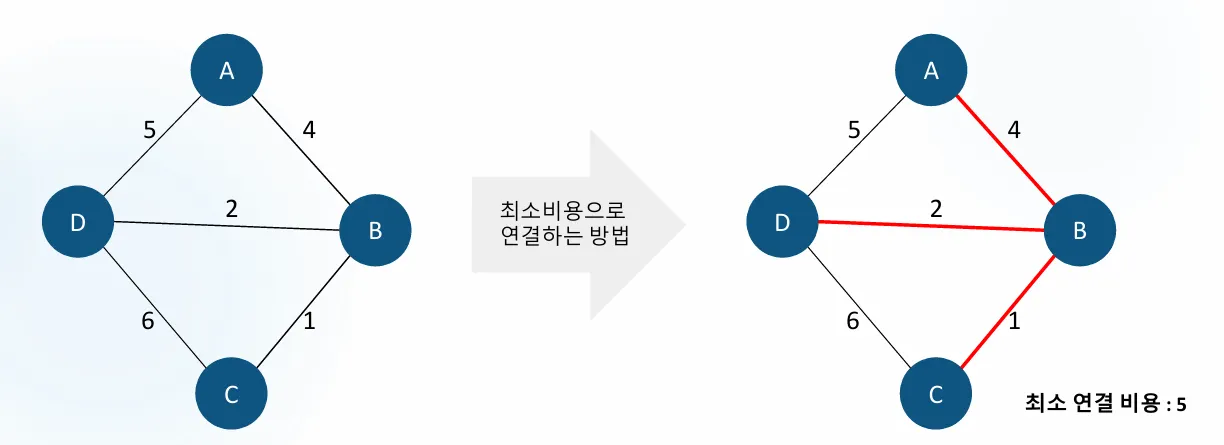
그래프에서 최소비용으로 모든 구간을 연결한 트리
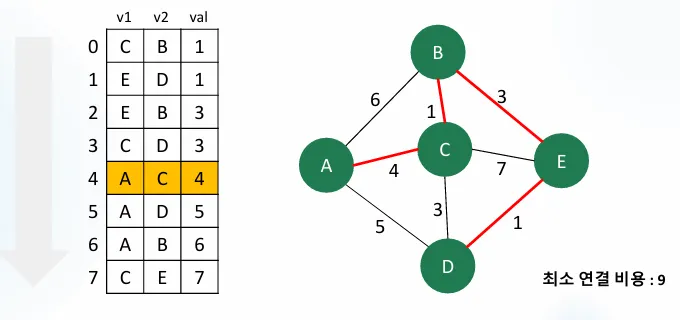
예시 그래프
MST의 특징
1.
트리이기 때문에 cycle 존재하면 안된다.
2.
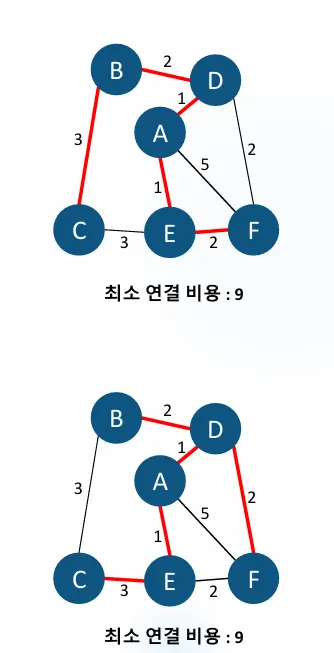
답은 여러개가 될 수 있다.
MST 예시 (복잡한 그래프)
KRUSKAL 알고리즘 요약
MST를 구하는 대표적인 알고리즘
시간복잡도는 O(N logN) 여기서 n은 엣지타는 간선의 수를 뜻한다.
크루스칼 알고리즘 과정
1.
가중치 값을 기준으로 정렬을 먼저 한다.
2.
Union Find 자료구조를 이용해서 간선을 선택해준다.
크루스칼 알고리즘 과정 1
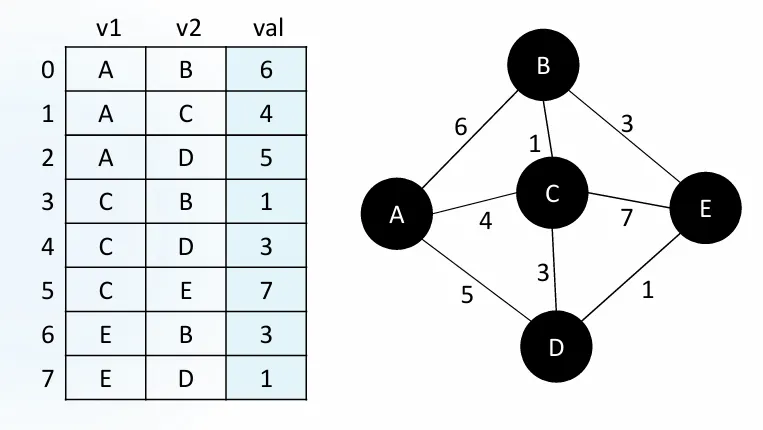
그래프를 아래와 같이 하드코딩 해준다.
v1과 v2의 순서는 반대여도 상관이 없다.
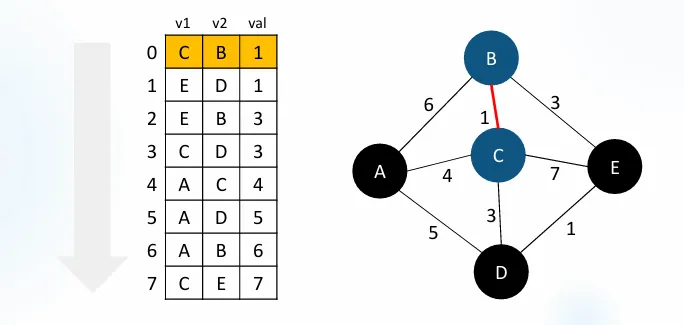
간선 리스트 표현
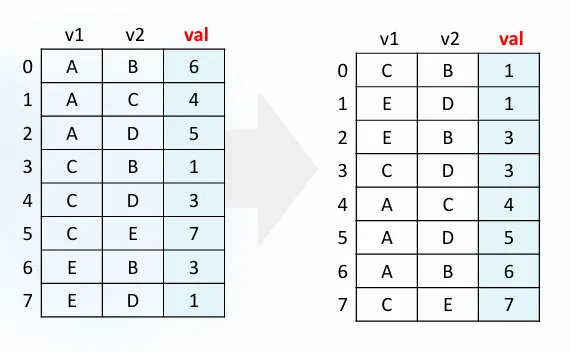
1. 정렬하기
가중치(val) 기준으로 오름차순 정렬:
2. 간선선택하기
단계별 진행 과정
1순 for문을 돌리면서 MST가 될 간선을 정정짓는다.
맨앞에 있는 C-B간선은 MST 간선으로 채택된다.
노드 C와 B는 같은 그룹이된다(Union Find알고리즘 사용)
1단계: C-B 간선 선택
C와 B가 같은 그룹으로 연결됨
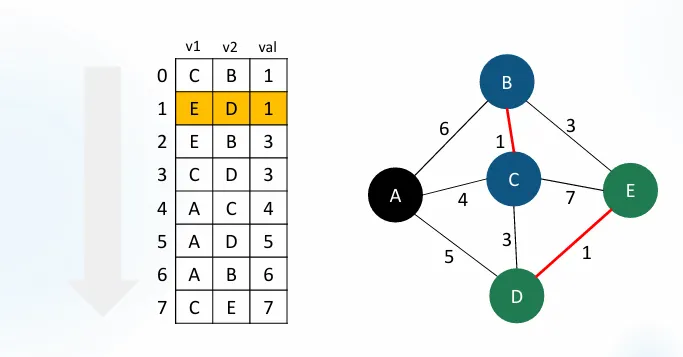
2단계: E-D 간선 확인
E-D 간선이 선택되고, E-D 가 같은 그룹인지 확인한후 아니라면 같은 그룹이 된다.
E-D는 간선 채택이 된다.
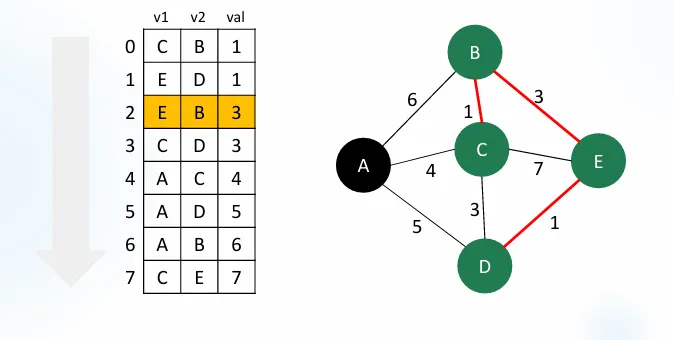
3단계: E-B 간선 확인
E-B에서 E,B는 각각 다른 그룹이기에 같은 그룹으로 만들고 간선 채택서진다.
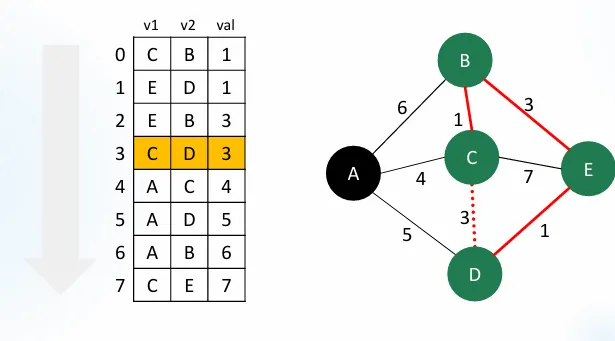
4단계: C-D 간선 확인
C-D는 같은 그룹이다. 같은 그룹인 노드를 연결시키면 Cycle이 발생하게 된다.
간선으로 채택하지 않고 넘어간다.
5단계: A-C 간선 선택
이와 같은 방법으로 나머지 간선정보들을 전부 순회시켜주면 MST가 완성된다.
MST 크루스칼 알고리즘 구현
완전한 소스코드
#include <iostream>
#include <algorithm>
#include <vector>
struct Node
{
char v1;
char v2;
int cost;
};
std::vector<Node> graph =
{
{'A', 'B', 6},
{'A', 'C', 4},
{'A', 'D', 5},
{'C', 'B', 1},
{'C', 'D', 3},
{'C', 'E', 7},
{'E', 'B', 3},
{'E', 'D', 1}
};
int n = 8; //간선의 갯수
bool compare(Node a, Node b)
{
return a.cost < b.cost;
}
int org[200] = {};
int findParent(int now)
{
if (org[now] == 0)
{
return now;
}
int ret = findParent(org[now]);
org[now] = ret;
return ret;
}
int unionOrg(int v1, int v2)
{
int p1 = findParent(v1);
int p2 = findParent(v2);
if (p1 == p2)
{
return 0;
}
org[p1] = p2;
return 1;
}
int main()
{
std::sort(graph.begin(), graph.end(), compare);
int cnt = 0;
int sum = 0;
for (size_t i = 0; i < graph.size(); i++)
{
if (unionOrg(graph[i].v1, graph[i].v2))
{
sum += graph[i].cost;
cnt++;
}
}
if (cnt == 4/*노드의개수 - 1 */)
{
std::cout << sum << std::endl;
}
return 0;
}
C++
복사
핵심 함수 분석
1. compare 함수
bool compare(Node a, Node b)
{
return a.cost < b.cost;
}
C++
복사
가중치 기준 오름차순 정렬용 비교함수
2. findParent 함수 (Union-Find)
int findParent(int now)
{
if (org[now] == 0)
{
return now;
}
int ret = findParent(org[now]);
org[now] = ret; // 경로 압축
return ret;
}
C++
복사
노드의 루트 부모를 찾는 함수 (경로 압축 최적화)
3. unionOrg 함수
int unionOrg(int v1, int v2)
{
int p1 = findParent(v1);
int p2 = findParent(v2);
if (p1 == p2)
{
return 0; // 같은 그룹 (사이클 발생)
}
org[p1] = p2; // 그룹 병합
return 1; // 병합 성공
}
C++
복사
두 노드를 같은 그룹으로 병합, 사이클 검사
BFS 길찾기 알고리즘
BFS 기본 특징
BFS(Breadth-First Search)는 그래프나 트리 구조에서 가장 가까운 노드부터 탐색하는 방식입니다.
•
큐(Queue) 자료구조를 사용합니다.
•
최단 경로를 찾는데 유용합니다.
•
시간복잡도는 O(V+E) 입니다. (V: 정점의 개수, E: 간선의 개수)
BFS 길찾기 구현
#include <iostream>
#include <queue>
#include <vector>
#include <tuple>
using namespace std;
const int dx[] = { -1, 1, 0, 0 };
const int dy[] = { 0, 0, -1, 1 };
//s -> 시작 좌표, e -> 도착 좌표
int bfs(const vector<vector<int>>& map, int sx, int sy, int ex, int ey)
{
int N = map.size();
int M = map[0].size();
vector<vector<bool>> visited(N, vector<bool>(M, false));
vector<vector<int>> dist(N, vector<int>(M, -1)); // 거리 배열
queue<pair<int, int>> q;
q.push({ sx, sy });
visited[sx][sy] = true;
dist[sx][sy] = 0;
while (!q.empty())
{
auto x = q.front().first;
auto y = q.front().second;
q.pop();
// 도착지 도달
if (x == ex && y == ey)
return dist[x][y];
for (int dir = 0; dir < 4; ++dir)
{
int nx = x + dx[dir];
int ny = y + dy[dir];
// 맵 내부 + 벽이 아님 + 미방문
if (nx >= 0 && nx < N && ny >= 0 && ny < M)
{
if (!visited[ny][nx] && map[ny][nx] == 0)
{
visited[ny][nx] = true;
dist[ny][nx] = dist[y][x] + 1;
q.push({ nx, ny });
}
}
}
}
return -1; // 도달 불가능
}
C++
복사
BFS 알고리즘 특징
핵심 요소
•
visited 배열: 방문 체크로 중복 방문 방지
•
dist 배열: 각 위치까지의 최단 거리 저장
•
4방향 탐색: dx, dy 배열로 상하좌우 이동
•
큐 사용: FIFO 구조로 레벨별 탐색
동작 과정
1.
시작점을 큐에 추가하고 방문 처리
2.
큐가 빌 때까지 반복:
•
큐에서 현재 위치 꺼내기
•
목표 도달시 거리 반환
•
4방향으로 이동 가능한 곳 탐색
•
조건 만족시 큐에 추가
장점과 활용
•
최단 경로 보장: 레벨별 탐색으로 최단 거리 찾기
•
격자 맵 탐색: 게임, 로봇 경로 계획
•
미로 찾기: 출구까지의 최단 경로
MST vs BFS 비교
구분 | MST (크루스칼) | BFS 길찾기 |
목적 | 최소 비용 연결 | 최단 경로 탐색 |
자료구조 | Union-Find | Queue |
시간복잡도 | O(E log E) | O(V + E) |
활용분야 | 네트워크 설계 | 경로 탐색 |
결과 | 최소 신장 트리 | 최단 거리 |
실무 활용 사례
MST 활용
•
네트워크 설계: 최소 비용으로 모든 도시 연결
•
클러스터링: 데이터 그룹핑
•
회로 설계: 최소 배선으로 모든 부품 연결
BFS 활용
•
게임 AI: 캐릭터 최단 이동 경로
•
네비게이션: 최단 거리 길찾기
•
소셜 네트워크: 친구 관계의 최단 연결
핵심 포인트
MST 크루스칼 알고리즘
1.
간선 정렬: 가중치 기준 오름차순
2.
Union-Find: 사이클 검사 및 그룹 관리
3.
간선 선택: 사이클 없이 최소 비용
4.
완성 조건: (노드 수 - 1)개의 간선
BFS 길찾기
1.
큐 활용: FIFO로 레벨별 탐색
2.
방문 체크: visited 배열로 중복 방지
3.
거리 기록: dist 배열로 최단 거리 저장
4.
4방향 탐색: 상하좌우 이동 처리
두 알고리즘 모두 그래프 문제 해결의 핵심 도구입니다.
“강의는 많은데, 왜 나는 아직도 코드를 못 짤까?”
혼자 공부하다 보면 누구나 이런 고민을 하게 됩니다.
•
강의는 다 들었지만 막상 손이 안 움직이고,
•
복습을 하려 해도 무엇을 다시 봐야 할지 모르겠고,
•
질문할 곳도 없고,
•
유튜브는 결국 정답을 따라 치는 것밖에 안 되는 것 같고.
문제는 ‘연습’이 빠졌기 때문입니다.
단순히 강의를 듣는 것만으로는 실력이 늘지 않습니다.
실제 문제를 풀고, 고민하고, 직접 구현해보는 시간이 반드시 필요합니다.
그래서, 얌얌코딩 코칭은 다릅니다.
그냥 가르치지 않습니다.
스스로 설계하고, 코딩할 수 있게 만듭니다.
얌얌코딩 코칭에서는 단순한 예제가 아닌,
스스로 문제를 분석하고 구현해야 하는 연습문제를 제공합니다.
이 연습문제들은 다음과 같은 역량을 키우기 위해 설계되어 있습니다:
•
문제를 스스로 쪼개고 설계하는 힘
•
다양한 조건을 만족시키는 실제 구현 능력
•
기능 단위가 아닌, 프로그램 단위로 사고하는 습관
•
마침내 자신의 힘으로 코드를 끝까지 작성하는 경험
지금 필요한 건 더 많은 강의가 아닙니다.
코드를 스스로 완성해 나가는 훈련,
그것이 지금 실력을 끌어올릴 가장 현실적인 방법입니다.
자세한 안내 보기: 프리미엄 코칭 안내 바로가기 또는 카카오톡 상담방: 얌얌코딩 상담방