선형 구조와 비선형 자료구조
선형 구조(Linear Structure)
데이터를 순차적으로 한 줄로 표기한 자료구조로 배열, 리스트, 스택, 큐가 있다.
순회하는 방법
•
반복문 (for, while) 사용
선형리스트 (Linear List)
데이터를 논리적인 순서에 따라서 메모리에 연속하여 저장하는 구현 방식을 의미하며, 주로 고정된 크기를 가진 배열을 통해 구현한다.
특징
•
그럼기 때문에 각 원소의 순서가 정해져 있으며, 각 원소의 인덱스를 사용할 수 있다
•
이로인해 데이터 검색에 효율적이지만, 삽입과 삭제 시 크기를 타 항목하거나, 모든 데이터를 이동해야하기 때문에 비효율적이다
핵심: 물리적 순서와 논리적 순서가 일치
링크드 리스트 (Linked List)
연결리스트는 노드를 통해 연결하는 리스트를 말한다.
특징
•
선형리스트와 달리 고정이 아닌, 가변적인 크기의 리스트를 가진다
•
따라서 데이터를 삽입, 제거 시 크기 할 당이나, 데이터를 이동할 필요 없이 다음 노드를 추가하거나, 제거할 수 있다
•
다만, 검색에 대해서는 선형리스트와 달리게 원하는 데이터를 한번에 찾아낼 수 없고, 리스트를 전부 탐색해 야 한다
사용 시기
•
주로 데이터 삽입, 제거가 많이 발생하는 프로그램이라면 연결리스트가 유리하고, 탐색에 주가 되는 프로그램이라면 선형리스트를 사용하는 것이 유리하다
스택 (Stack)
스택은 한쪽으로만 데이터를 넣고 뺄 수 있는 구조의 자료구조이다.
시각적 표현
┌───┐
│ 4 │ ← top (가장 나중에 들어온 것)
├───┤
│ 3 │
├───┤
│ 2 │
├───┤
│ 1 │ ← bottom (가장 먼저 들어온 것)
└───┘
Plain Text
복사
특징
•
그럼기 때문에 마지막에 넣은 데이터가 가장 먼저 나가는 LIFO (Last-In First-Out) 구조를 가진다
•
주로 연결리스트를 통해 구현하고, 컴파일우리의 페이지 되돌아기, undo, 문자열 뒤집기와 같은 프로그램에 사용된다
큐 (Queue)
큐는 양쪽으로 데이터를 넣고 뺄 수 있는 자료구조이다.
시각적 표현
← 제거 [1][2][3][4] 추가 →
(front) (rear)
Plain Text
복사
특징
•
큐의 중류에 따라 차이점이 있지만, 기본적인 큐는 한쪽으로 데이터를 넣고, 다른 한쪽으로 데이터를 뺄 수 있다
•
따라서 가장 먼저 들어온 데이터가 가장 먼저 나오는 FIFO (First-In First-Out) 구조를 가진다
•
큐는 일반적으로 연결리스트를 통해 구현하며, 선입선출을 필요로 하는 대기열, 프로세스 관리, 너비 우선 탐색에 사용된다
트리 (Tree)
트리는 노드가 나무 가지처럼 연결되어 있는 비선형 자료구조이다.
시각적 표현
특징
•
마치 나무를 뒤집어 놓은 모습과 유사하다
•
트리 내 또 다른 하위 트리가 있고, 그 안에도 또 다른 하위 트리가 있는 재귀적인 구조를 가진다
•
컴퓨터의 디렉토리 구조가 트리 구조이다
주요 용어
•
루트(Root): 트리의 최상단 노드
•
부모 노드(Parent): 상위 노드
•
자식 노드(Child): 하위 노드
•
잎 노드(Leaf): 자식이 없는 노드
그래프 (Graph)
그래프는 노드와 노드를 연결하는 간선을 모아놓는 자료구조이다.
시각적 표현
트리와 그래프의 차이점
•
트리와 많이 비교가 되는데 트리 역시 그래프의 형태이나, 그래프는 방향이 있거나, 없을 수 있으며, 루트 노드라는 개념이 없다. 또한 사이클이 가능한 형태로 구성되어 있다
순회하는 방법
그래프 순회 알고리즘
•
DFS, BFS 알고리즘 사용
그래프 표현 방법
그래프를 표현할 때는 인접행렬과 연결리스트를 사용하는 방식이 있다.•
보통 알고리즘 문제를 풀 때는 있어서는 인접행렬을 활용한 방식을 많이 사용한다
•
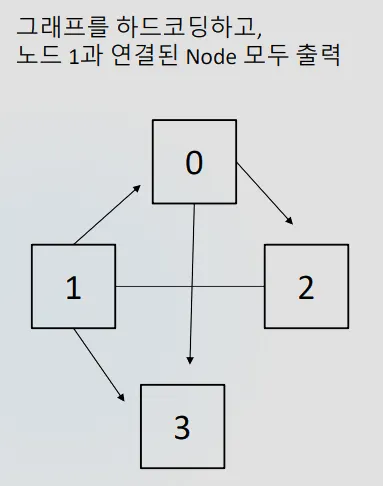
다음은 인접행렬을 이용해 그래프를 표현하고 1번 노드가 연결되어있는 다른노드의 종류를 표현하는 예제 코드이다
그래프 구현 예제
#include <iostream>
int main()
{
// 4x4 인접행렬로 그래프 표현
int map[4][4] =
{
0, 0, 1, 1, // 노드 0: 2, 3과 연결
1, 0, 1, 1, // 노드 1: 0, 2, 3과 연결
0, 1, 0, 0, // 노드 2: 1과 연결
0, 0, 0, 0, // 노드 3: 연결 없음
};
for (size_t j = 0; j < 4; j++)
{
std::cout << j << "번 노드 이동가능 : ";
for (size_t i = 0; i < 4; i++)
{
if (map[j][i] != 0) // 연결되어 있다면
{
std::cout << i << "번, ";
}
}
std::cout << std::endl;
}
return 0;
}
C++
복사
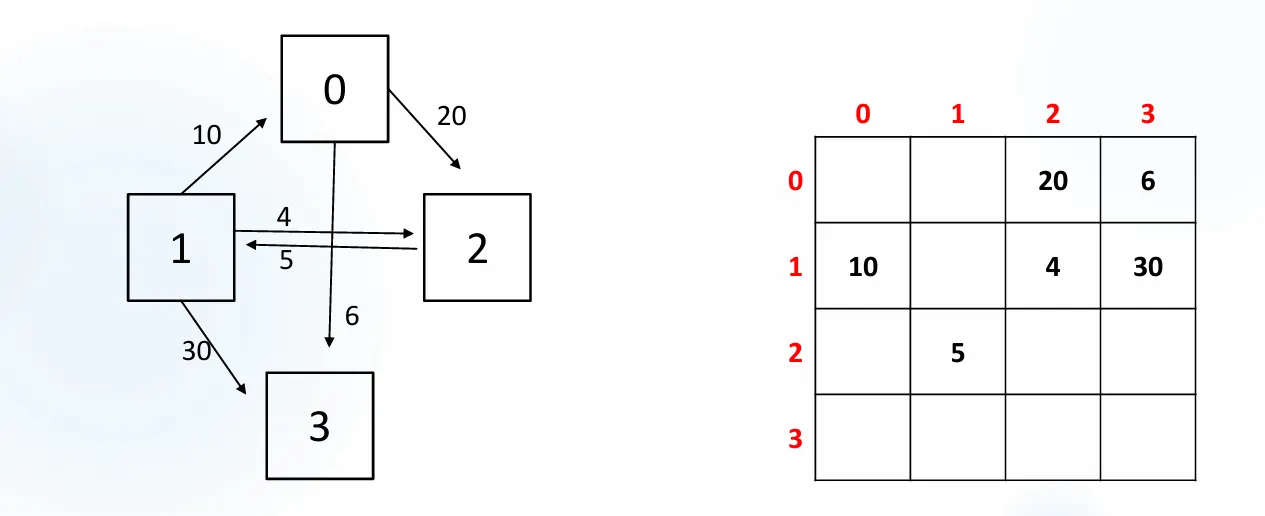
가중치가 있는 그래프
그래프 시각화:
핵심 정리
선형 자료구조
구조 | 특징 | 주요 연산 | 사용 예시 |
배열 | 연속 메모리, 인덱스 접근 | 읽기 O(1), 삽입/삭제 O(n) | 정적 데이터 저장 |
연결리스트 | 동적 크기, 포인터 연결 | 삽입/삭제 O(1), 검색 O(n) | 동적 데이터 관리 |
스택 | LIFO 구조 | push/pop O(1) | 함수 호출, Undo 기능 |
큐 | FIFO 구조 | enqueue/dequeue O(1) | 작업 대기열, BFS |
비선형 자료구조
구조 | 특징 | 순회 방법 | 사용 예시 |
트리 | 계층적 구조, 루트 존재 | 전위/중위/후위 순회 | 파일 시스템, 검색 트리 |
그래프 | 네트워크 구조, 사이클 가능 | DFS/BFS | 지도, 네트워크, SNS |
연습문제 해결 접근법
연습문제: 각 노드가 갈 수 있는 노드번호와 비용을 출력해 전부 해보자!
해결 단계
1.
인접행렬 분석: 각 행을 순회하며 0이 아닌 값 찾기
2.
연결 정보 출력: 노드 번호와 가중치 함께 출력
3.
모든 노드 순회: 전체 그래프 구조 파악
핵심 아이디어:
•
이차원 배열 map[i][j]에서 i는 시작 노드, j는 도착 노드
•
값이 0이 아니면 연결되어 있으며, 그 값이 가중치(비용)
이렇게 선형과 비선형 자료구조의 기본 개념과 구현 방법을 이해하면, 복잡한 알고리즘 문제도 효율적으로 해결할 수 있습니다!
“강의는 많은데, 왜 나는 아직도 코드를 못 짤까?”
혼자 공부하다 보면 누구나 이런 고민을 하게 됩니다.
•
강의는 다 들었지만 막상 손이 안 움직이고,
•
복습을 하려 해도 무엇을 다시 봐야 할지 모르겠고,
•
질문할 곳도 없고,
•
유튜브는 결국 정답을 따라 치는 것밖에 안 되는 것 같고.
문제는 ‘연습’이 빠졌기 때문입니다.
단순히 강의를 듣는 것만으로는 실력이 늘지 않습니다.
실제 문제를 풀고, 고민하고, 직접 구현해보는 시간이 반드시 필요합니다.
그래서, 얌얌코딩 코칭은 다릅니다.
그냥 가르치지 않습니다.
스스로 설계하고, 코딩할 수 있게 만듭니다.
얌얌코딩 코칭에서는 단순한 예제가 아닌,
스스로 문제를 분석하고 구현해야 하는 연습문제를 제공합니다.
이 연습문제들은 다음과 같은 역량을 키우기 위해 설계되어 있습니다:
•
문제를 스스로 쪼개고 설계하는 힘
•
다양한 조건을 만족시키는 실제 구현 능력
•
기능 단위가 아닌, 프로그램 단위로 사고하는 습관
•
마침내 자신의 힘으로 코드를 끝까지 작성하는 경험
지금 필요한 건 더 많은 강의가 아닙니다.
코드를 스스로 완성해 나가는 훈련,
그것이 지금 실력을 끌어올릴 가장 현실적인 방법입니다.
자세한 안내 보기: 프리미엄 코칭 안내 바로가기 또는 카카오톡 상담방: 얌얌코딩 상담방