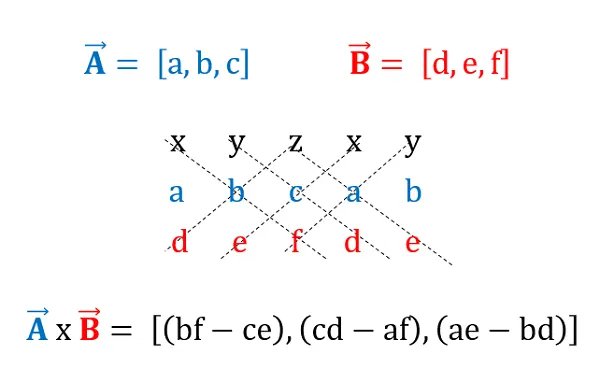/////
Search
Duplicate
📄

벡터 리포트

스칼라와 벡터

스칼라

•
방향이 없는 값
•
값만 가짐 ex) 속력

벡터

•
방향이 있는 값
•
방향과 값을 같이 가짐 ex) 속도
•
게임프로그래밍에 있어 벡터는 좌표처럼 사용된다.
•
벡터는 행렬로도 표기할 수 있음
(1,2) = [12]\begin{bmatrix} 1\\ 2 \end{bmatrix}
•
벡터와 행렬은 밀접한 관계에 있음

벡터의 크기

•
벡터는 피타고라스의 정의로 크기를 알 수 있다.
•
(a2+b2)=c2\sqrt{(a^2 + b^2)} = \sqrt{c^2}
•
프로그래밍에서 루트 연산은 꽤 큰 비용을 차지하므로 대체로 루트 연산을 생략한다.

영벡터

•
모든 원소의 값이 0인 벡터
•
유일하게 방향이 없다.
•
해당 벡터는 점으로 표현 가능

단위 벡터

•
크기가 1인 벡터
•
방향만을 알고 싶을 때 사용
•
벡터를 정규화하면 얻을 수 있다.
•
벡터의 정규화 공식은 아래와 같다.
•
normalized(a)=a∣∣a∣∣=aax2+ay2normalized(a) = \frac{a}{||a||} = \frac{a}{\sqrt{{a_x}^2 + {a_y}^2}}

벡터의 덧셈과 뺄셈

•
벡터끼리는 아래의 형태로 더하고 뺄 수 있음
•
교환법칙 성립
•
(1,2)+(3,4)=(4,6)(1,2)−(3,4)=(−2,−2)(1,2) + (3,4) = (4,6) \\ (1,2) - (3,4) = (-2,-2)
•
같은 위치의 값끼리 더하면 된다.

벡터의 스칼라 곱

•
벡터는 스칼라와 곱할 수 있음
•
k×(1,2)=(1,2)×k=(k,2k)k \times (1,2) = (1,2) \times k = (k, 2k)

벡터와 벡터의 곱셈

•
벡터간의 곱은 내적과 외적이다.

벡터의 내적

•
벡터의 내적은 결과값으로 스칼라값이 나온다
•
공식은 아래와 같다.
•
a⋅b=∑i=1naibi=axbx+aybya \cdot b = \sum\limits_{i=1}^na_ib_i = a_xb_x + a_yb_y
•
삼각함수를 이용하면 아래와 같이 표현할 수 있다.
•
a⋅b=∣a∣∣∣b∣cosθa \cdot b = |a|||b|cos\theta
•
게임에서는 대체로 삼각함수를 이용한 공식을 사용한다.
•
내적은 분배 법칙이 성립
•
활용 방법은 아래와 같다.

1. 내 위치에서 상대의 위치를 알고 싶을 때

•
내 벡터와 상대의 벡터를 내적 후 나온 값으로 상대가 어느 위치에 있는지 알 수 있다.
•
a⋅b>0a \cdot b > 0 ⇒ 상대가 내 앞에 있다.
•
a⋅b=0a \cdot b = 0 ⇒ 상대가 내 벡터와 수직으로 있다 (내 옆에 있다)
•
a⋅b<0a \cdot b < 0 ⇒ 상대가 내 뒤에 있다.
•
값의 부호에 따라 달라지는 이유는 coscos그래프를 보면 알 수 있다.

2. 두 벡터의 각도

•
위 1번 예시에서 cos의 값을 알 수 있으므로 θ\theta값(각도)를 알 수 있다.
•
나온 값을 cos의 역함수인 arccos에 넣으면 각도를 알 수 있다.
•
θ=arccos(a⋅b∥a∥∥b∥)θ=arccos(a^⋅b^)\theta = arccos(\frac{a \cdot b}{\Vert a \Vert \Vert b \Vert})\\ \theta = arccos(\hat{a} \cdot \hat{b})
•
각도를 구할 때 Atan2 함수를 이용하면 동일한 결과를 얻으나 단위 벡터를 구한 후 내적하여 계산하는 방식이 효율적

3. 시야각

•
1번과 2번을 이용하여 설정한 시야각 내에 물체가 존재하는지 판별할 수 있다.
•
방법은 아래와 같다.
1.
시야각을 절반으로 나눈 각의 cos 값을 계산 ⇒ FF
2.
캐릭터와 물체의 단위 벡터를 구한 후 해당 값을 내적
a.
캐릭터의 단위 벡터를 ff
b.
물체의 단위 벡터를 vv
3.
f⋅v≥Ff \cdot v \geq F ⇒ 물체가 시야각 내에 존재한다.
4.
f⋅v<Ff \cdot v < F ⇒ 물체가 시야각 내에 존재하지 않는다.

벡터의 외적

•
cross product라고도 하며 각 원소를 교하여 빼는 방식의 연산
•
이에 대한 이해를 돕는 그림은 아래와 같다
•
외적은 새로운 벡터를 결과 값으로 반환
•
외적으로 나온 벡터는 연산에 사용한 A벡터와 B벡터에 수직인 벡터가 나온다.
•
외적으로 생성된 벡터의 길이는 A벡터와 B벡터의 사이 각의 sinθsin\theta와 같다.
•
∥a∥×∥b∥=∥a∥∥b∥sinθ \Vert a \Vert \times \Vert b\Vert = \Vert a\Vert \Vert b \Vert sin\theta
•
외적은 결합법칙, 교환법칙 모두 성립하지 않는다.
•
수직인 벡터의 방향은 두가지가 존재하며 이를 게임 프로그래밍에서 활용한다.

1. 두 벡터가 평행 한가?

•
두 벡터를 외적하였을 때 크기가 0인 벡터가 나온다면 평행한 벡터이다.

2. 좌우 판별

•
플레이어와 물체의 벡터를 외적 하였을 때 나온 벡터와 플레이어의 윗방향을 가르키는 단위 벡터를 내적 하였을 때 값의 부호에 따라 좌우를 알 수 있다.
•
수식 : up⋅(A×B)up \cdot (A \times B)
이는 좌표계에 따라 좌우가 반전될 수 있음을 유의하여야 한다.
•
왼손좌표계 기준의 결과
◦
up⋅(A×B)>0up \cdot (A \times B) > 0 : 물체가 내 오른쪽에 있음
◦
up⋅(A×B)<0up \cdot (A \times B) < 0 : 물체가 내 왼쪽에 있음
Made with