LV16 트리(tree), 그래프(graph) DFS 순회

트리(Tree) 자료구조

트리란?

트리(Tree)란 노드들이 나무 가지처럼 연결되어 있는 비선형 계층적 자료구조이다.

•

트리는 다음과 같이 나무를 거꾸로 뒤집어 놓은 모양과 유사하다

•

트리는 또한 트리 내에 다른 하위 트리가 있고 그 하위 트리 안에도 또 다른 하위 트리가 있는 재귀적인 자료구조이기도 합니다

트리의 조건

트리의 조건:

단방향 그래프

Cycle이 없어야함

부모 자식관계인 그래프(정확히, 두 노드 간의 연결선이 유일한 그래프)

실생활 예시

컴퓨터의 directory구조가 트리 구조의 대표적인 예가 될 수 있습니다.

                      root
                        /
        ┌──────────────────────────────────────────┐
     /bin/  /boot/  /dev/  /etc/  /home/  /lib/  /media/  /mnt/
        │
    ┌───┴───┬───┬───┬───┬───┬───┬───┐
   /opt/  /root/ /sbin/ /srv/ /tmp/ /usr/ /var/
                                    │
                        ┌───────────┼───────────┐
                    /bin/ /include/ /lib/ /sbin/ /cache/ /log/ /spool/ /tmp/
Plain Text
복사

트리 구조에서 사용되는 기본 용어

기본 개념

•

노드 (Node): 트리를 구성하고 있는 기본 요소

•

노드에는 키 또는 값과 하위 노드에 대한 포인터를 가지고 있음

•

A, B, C, D, E, F, G, H, I, J

노드 관계

•

간선 (Edge): 노드와 노드 간의 연결선

•

루트 노드 (Root Node): 트리 구조에서 부모가 없는 최상위 노드

◦

root node : A

•

부모 노드 (Parent Node): 자식 노드를 가진 노드

◦

H, I에 부모 노드는 D

•

자식 노드 (Child node): 부모 노드의 하위 노드

◦

노드 D의 자식 노드는 H, I

•

형제 노드 (Sibling node): 같은 부모를 가지는 노드

◦

H, I는 같은 부모를 가지는 형제 노드

노드 분류

•

외부 노드(external node, outer node), 단말 노드 (terminal node), 리프 노드(leaf node)

◦

자식 노드가 없는 노드

◦

H, I, J, F, G

•

내부 노드 (internal node, inner node), 비 단말 노드 (non-terminal node), 가지 노드 (branch node)

◦

자식 노드 하나 이상 가진 노드

◦

A, B, C, D, E

트리 속성

•

깊이 (depth): 루트에서 어떤 노드까지의 간선(Edge) 수

◦

루트 노드의 깊이 : 0

◦

D의 깊이 : 2

•

높이 (height): 어떤 노드에서 리프 노드까지 가장 긴 경로의 간선(Edge) 수

◦

리프 노드의 높이 : 0

◦

A 노드의 높이 : 3

트리 종류

편향 트리 (Skew Tree)

•

모든 노드들이 자식을 하나만 가진 트리

•

왼쪽 방향으로 자식을 하나씩만 가질 때 left skew tree, 오른쪽 방향으로 하나씩만 가질 때 right skew tree라고 함

이진트리 (Binary Tree)

•

각 노드의 차수(자식 노드)가 2 이하인 트리

이진 탐색 트리 (Binary Search Tree, BST)

•

순서화된 이진 트리

•

노드의 왼쪽 자식은 부모의 값보다 작은 값을 가져야 하며 노드의 오른쪽 자식은 부모의 값보다 큰 값을 가져야 함

m원 탐색 트리(m-way search tree)

•

최대 m개의 서브 트리를 갖는 탐색 트리

•

이진 탐색 트리의 확장된 형태로 높이를 줄이기 위해 사용함

균형 트리 (Balanced Tree, B-Tree)

•

m원 탐색 트리에서 높이 균형을 유지하는 트리

•

height-balanced m-way tree라고도 함

사용 사례

계층적 데이터 저장

•

트리는 데이터를 계층 구조로 저장하는 데 사용됩니다

•

예를 들어 파일 및 폴더는 계층적 트리 형태로 저장됩니다

효율적인 검색 속도

•

효율적인 삽입, 삭제 및 검색을 위해 트리 구조를 사용합니다

힙(Heap)

•

힙도 트리로 된 자료 구조입니다

데이터 베이스 인덱싱

•

데이터베이스 인덱싱을 구현하는데 트리를 사용합니다

•

예) B-Tree, B+Tree, AVL-Tree..

Trie

•

사전을 저장하는 데 사용되는 특별한 종류의 트리입니다

트리 하드코딩 하기

인접행렬로 표현하는 경우

트리 구조:

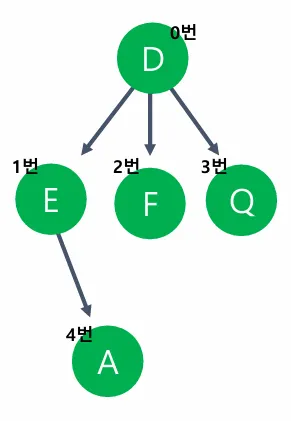
       D(0번)
      / | \
   E(1) F(2) Q(3)
   /
 A(4)
Plain Text
복사

인접행렬 표현:

char value[5] = { 'D', 'E', 'F', 'Q', 'A' };
int matrix[5][5] =
{
    0,1,1,1,0,   // D → E, F, Q 연결
    0,0,0,0,1,   // E → A 연결
    0,0,0,0,0,   // F 연결 없음
    0,0,0,0,0,   // Q 연결 없음
    0,0,0,0,0,   // A 연결 없음
};
C++
복사

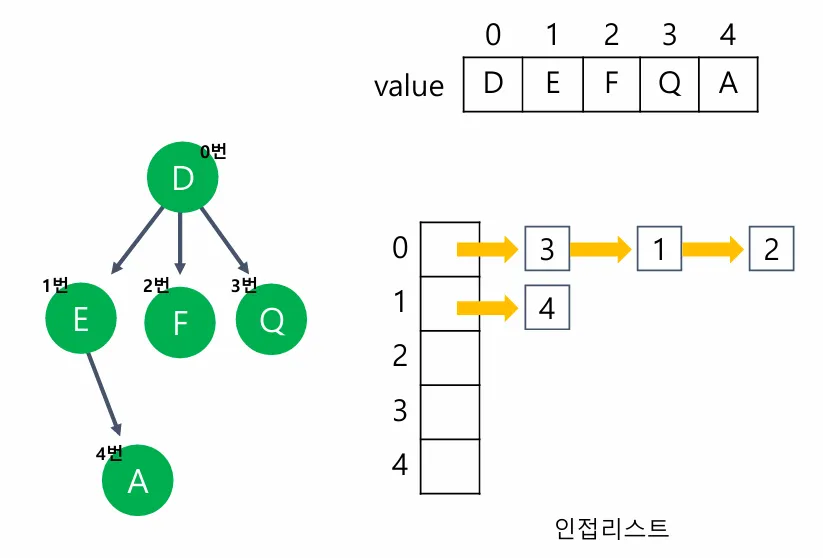
리스트로 표현하는 경우

인접리스트:

→ 3 → 1 → 2
→ 4



Plain Text
복사

1차원 배열로 표현하는 경우

2진트리의 경우 1차원배열로도 표현 가능하다:

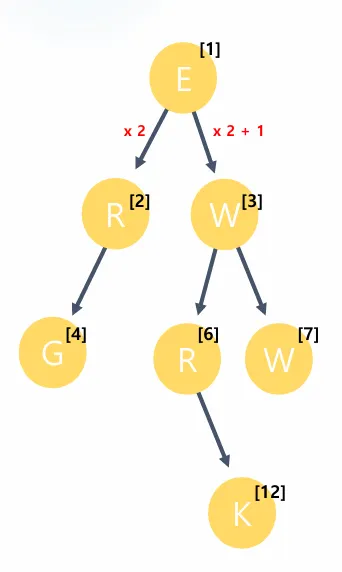
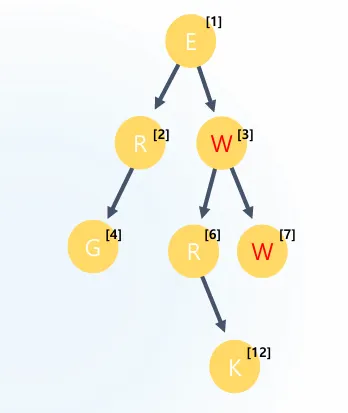
char map[256] = " ERWG RW    K ";

// 배열 인덱스와 트리 노드 관계:
//     E[1]
//    /    \
//  R[2]   W[3]
//  /  \   /  \
// G[4] [5]R[6] W[7]
//            \
//            K[12]

// rootNode를 1번으로
// 왼쪽자식은 부모 index * 2
// 오른쪽 자식은 부모 index *2 + 1
C++
복사

char map[256] = " ERWG RW    K";
Python
복사

인덱스 계산 공식:

•

왼쪽 자식: parent_index * 2

•

오른쪽 자식: parent_index * 2 + 1

•

부모: child_index / 2

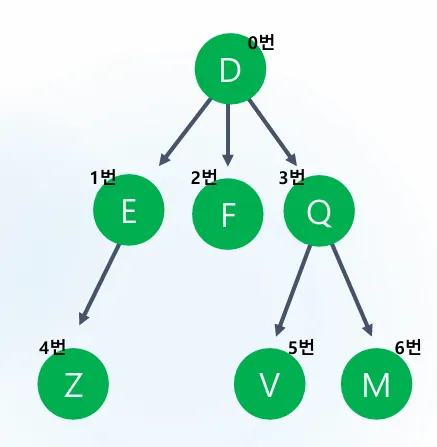
자식노드 출력해보기

#include<iostream>

int main()
{
    char value[10] = "DEFQZVM";
    int map[7][7] =
    {
        0,1,1,1,0,0,0,
        0,0,0,0,1,0,0,
        0,0,0,0,0,0,0,
        0,0,0,0,0,1,1,
        0,0,0,0,0,0,0,
        0,0,0,0,0,0,0,
        0,0,0,0,0,0,0,
    };

    int n = 0;
    std::cin >> n;

    for (size_t i = 0; i < 7; i++)
    {
        if (map[n][i] > 0)
        {
            std::cout << value[i] << std::endl;
        }
    }

    return 0;
}
C++
복사

동작: 입력받은 노드 번호에 자식노드들을 전부 출력해보자.

부모 노드 출력 해보기

#include<iostream>

int main()
{
    char map[15] = " ERMG RW    K ";

    int n = 0;
    std::cin >> n;

    std::cout << map[n / 2] << std::endl;

    return 0;
}
C++
복사

동작: 1차원 배열로 구현된 트리에서 부모 노드 찾기

트리 순회와 DFS 연결

트리의 순회 방법 2가지

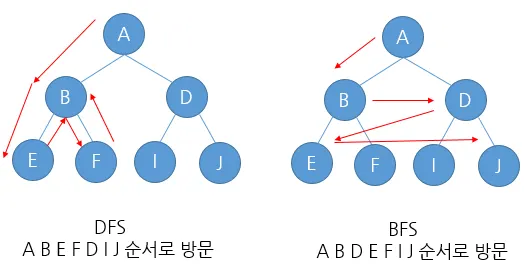
DFS
 재귀호출,스택을 사용하여 노드를 탐색한다. Depth First Search(깊이 우선 탐색)
 노드를 깊숙히 안쪽으로 들어가면서 탐색한다.
 트리,그래프 둘다 연습해야한다.

BFS
큐를 이용하여 , 노드를 탐색한다. Breadth First Search(너비 우선 탐색)
노드의 레벨 또는 너비를 우선적으로 탐색한다.
 트리,그래프 둘다 연습해야한다.

 트리냐 그래프냐에 따라서 큰 순회방법은 비슷하지만
 특정조건이 들어갈수 있기때문에 구현방법이 달라질수 있다.
Plain Text
복사

핵심 정리

트리 vs 그래프 차이점

구분	트리	그래프
사이클	없음	있을 수 있음
루트	하나의 루트 존재	루트 개념 없음
방향성	부모→자식 (단방향)	양방향/단방향 가능
연결성	모든 노드 연결	연결되지 않은 노드 가능

표현 방법 비교

방법	장점	단점	적합한 경우
인접행렬	구현 간단, 빠른 연결 확인	메모리 낭비	작은 트리, 완전 트리
인접리스트	메모리 효율적	구현 복잡	큰 트리, 희소 트리
1차원 배열	매우 간단	완전 이진트리만 가능	힙, 완전 이진트리

활용 분야

•

 파일 시스템: 디렉토리 구조

•

 검색 엔진: 인덱싱 구조

•

 데이터베이스: B-Tree 인덱스

•

 언어 처리: 구문 분석 트리

•

 게임: 의사결정 트리

트리는 계층적 구조를 효율적으로 표현하고 관리할 수 있는 핵심적인 자료구조입니다!

1. 트리 순회 (Tree Traversal)

기본 개념

•

트리: 사이클이 없는 연결 그래프

•

DFS: 한 방향으로 끝까지 가서 탐색 후 되돌아가기

DFS란 무엇인가?

DFS(Depth First Search, 깊이 우선 탐색)는 그래프나 트리를 탐색하는 기본 알고리즘입니다.

핵심 아이디어:

•

한 경로를 끝까지(깊이 우선) 탐색합니다

•

더 이상 갈 곳이 없으면 뒤로 돌아와서(백트래킹) 다른 경로를 탐색합니다

•

재귀 함수 또는 스택으로 구현합니다.

비유:

•

미로를 탐험할 때 한 길을 끝까지 가보고, 막다른 길이면 돌아와서 다른 길을 시도하는 것과 같습니다

•

책의 목차를 읽을 때 1장 → 1.1절 → 1.1.1항 순서로 깊이 들어갔다가, 다시 1.1.2항으로 이동하는 것과 같습니다

코드 구조

#include <iostream>

char value[6] = "TBECD";
char path[6] = "";

int map[5][5] =
{
    0,1,1,0,0,
    0,0,0,1,1,
    0,0,0,0,0,
    0,0,0,0,0,
    0,0,0,0,0,
};

void run(int now, int level)
{
    std::cout << value[now];

    for (size_t i = 0; i < 5; i++)
    {
        if (map[now][i] == 1)
        {
            path[level + 1] = value[i];
            run(i, level + 1);
            path[level + 1] = 0;
        }
    }
}

int main()
{
    path[0] = value[0];
    run(0, 0);

    return 0;
}
C++
복사

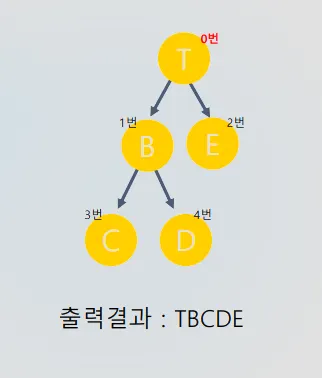
실행 결과: T → B → C → D → E (TBCDE)

코드 동작 분석

라인별 상세 설명:

void run(int now, int level)
{
    std::cout << value[now];  // ① 현재 노드 출력

    for (size_t i = 0; i < 5; i++)  // ② 모든 자식 노드 확인
    {
        if (map[now][i] == 1)  // ③ 연결된 자식이 있는가?
        {
            path[level + 1] = value[i];  // ④ 경로 기록
            run(i, level + 1);  // ⑤ 재귀 호출 (깊이 우선!)
            path[level + 1] = 0;  // ⑥ 백트래킹 후 경로 초기화
        }
    }
}
C++
복사

실행 흐름 (단계별):

T(0) 방문 → 출력: T

•

자식 확인: B(1), E(2) 발견

•

B(1)부터 탐색 시작

B(1) 방문 (T의 첫 번째 자식) → 출력: B

•

자식 확인: C(3), D(4) 발견

•

C(3)부터 탐색 시작

C(3) 방문 (B의 첫 번째 자식) → 출력: C

•

자식 없음 → 돌아감 (백트래킹)

D(4) 방문 (B의 두 번째 자식) → 출력: D

•

자식 없음 → 돌아감 (백트래킹)

E(2) 방문 (T의 두 번째 자식) → 출력: E

•

자식 없음 → 탐색 종료

최종 출력: TBCDE

DFS의 핵심 특징

장점:

•

구현이 간단합니다 (재귀 사용)

•

경로를 저장하면서 탐색 가능

•

백트래킹 문제에 적합

•

메모리 사용이 적습니다 (현재 경로만 저장)

단점:

•

최단 경로를 보장하지 않습니다

•

깊이가 너무 깊으면 스택 오버플로우 위험

•

모든 경로를 탐색하므로 비효율적일 수 있음

DFS가 유용한 경우:

•

모든 경로를 탐색해야 할 때

•

백트래킹이 필요한 문제 (미로 찾기, 순열 생성 등)

•

사이클 감지

•

위상 정렬

•

연결 요소 찾기

2. 배열 기반 트리 표현

•

1차원 배열로 이진트리 표현

•

인덱스 규칙: 왼쪽 자식(now * 2), 오른쪽 자식(now * 2 + 1)

코드

#include <iostream>

char tree[256] = " TBECD";


void run(int now, int level)
{
    if (tree[now] == '\0')  // 종료 조건: 빈 노드
    {
        return;
    }

		std::cout << tree[now];  // 현재 노드 출력
    run(now * 2, level + 1);  // 왼쪽 자식 탐색
    run(now * 2 + 1, level + 1);  // 오른쪽 자식 탐색
}

int main()
{
    run(1, 0);  // 인덱스 1부터 시작 (루트 노드)

    return 0;
}
C++
복사

배열 기반 트리 순회 설명

트리 구조 (인덱스):

실행 순서 (Pre-order):

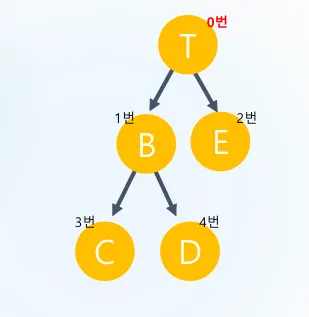
T[1] 출력 → T

왼쪽 자식 B[2] 탐색

•

B[2] 출력 → B

•

왼쪽 자식 C[4] 탐색

◦

C[4] 출력 → C

◦

C의 자식들은 '0' (없음)

•

오른쪽 자식 D[5] 탐색

◦

D[5] 출력 → D

◦

D의 자식들은 '0' (없음)

오른쪽 자식 E[3] 탐색

•

E[3] 출력 → E

•

E의 자식들은 '0' (없음)

최종 출력: TBECD

인덱스 계산의 비밀:

•

부모가 i일 때:

◦

왼쪽 자식 = i * 2

◦

오른쪽 자식 = i * 2 + 1

•

자식이 i일 때:

◦

부모 = i / 2

3. 그래프 순회 (Graph Traversal)

핵심 차이점

•

사이클 존재 가능 → visited[] 배열 필수

•

중복 방문 방지가 핵심

코드 구조

#include <iostream>

char value[10] = "TEQWA";
int map[5][5] = 
{
    {0, 1, 0, 0, 0},
    {0, 0, 1, 1, 0},
    {0, 0, 0, 0, 0},
    {1, 0, 0, 0, 1},
    {0, 0, 0, 0, 0}
};
int visited[10] = { 0, };  // 방문 표시
char path[10] = { 0, };     // 경로 저장


void run(int now, int level)
{
    std::cout << value[now];

    for (size_t i = 0; i < 5; i++)
    {
        if (map[now][i] == 1 && visited[i] == 0)  // 연결되고 미방문
        {
            path[level + 1] = value[i];
            visited[i] = 1;              // ★ 방문 표시
            run(i, level + 1);
            path[level + 1] = 0;
        }
    }
}

int main()
{
    path[0] = 'T';
    visited[0] = 1;    // 시작점 방문 표시
    run(0, 0);

    return 0;
}
C++
복사

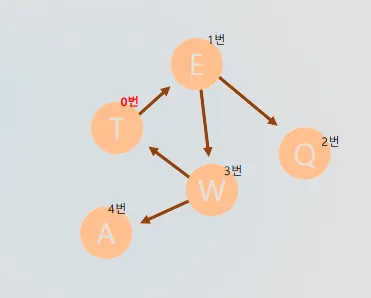
그래프 예시

•

노드: T, E, Q, W, A

•

연결 관계: T가 시작, 각 노드들이 상호 연결

•

탐색 순서: visited 배열에 따라 결정

그래프 DFS 상세 실행 과정

인접 행렬 분석:

실행 흐름:

초기화: visited[0] = 1 (T 방문 표시)

T(0) 탐색 시작 → 출력: T

•

E(1) 발견, 미방문

•

visited[1] = 1, E로 이동

E(1) 탐색 → 출력: E

•

Q(2) 발견, 미방문

•

visited[2] = 1, Q로 이동

Q(2) 탐색 → 출력: Q

•

연결된 미방문 노드 없음

•

E로 백트래킹

E(1) 계속 (Q 다음)

•

W(3) 발견, 미방문

•

visited[3] = 1, W로 이동

W(3) 탐색 → 출력: W

•

T(0) 발견, 이미 방문 (visited[0] = 1) → 무시 

•

A(4) 발견, 미방문

•

visited[4] = 1, A로 이동

A(4) 탐색 → 출력: A

•

연결된 미방문 노드 없음

•

탐색 종료

최종 출력: TEQWA

visited 배열의 역할:

•

W에서 T로 다시 가려는 순간, visited[0] = 1을 확인

•

이미 방문했으므로 무시 → 무한 루프 방지!

4. 핵심 비교

구분	트리 DFS	그래프 DFS
사이클	없음	있을 수 있음
visited 배열	불필요	필수
복잡도	간단	중복 체크 필요

5. 중요 포인트

반드시 기억할 것

재귀 구조: 작은 문제로 나눠서 해결

visited 배열: 그래프에서 무한루프 방지의 핵심

초기화: visited[시작점] = 1 잊지 말기

코딩 주의사항

•

배열 범위 체크

•

재귀 종료조건 명확히

•

visited 배열 올바른 사용

6. 시간/공간 복잡도

시간 복잡도

트리 DFS: O(N)

•

N: 노드의 개수

•

모든 노드를 정확히 한 번씩 방문

•

각 노드에서 자식 확인: O(자식 수)

그래프 DFS:

•

인접 행렬: O(V²)

◦

V: 정점(vertex) 개수

◦

각 정점에서 모든 정점 확인 필요

•

인접 리스트: O(V + E)

◦

V: 정점 개수, E: 간선(edge) 개수

◦

각 정점과 연결된 간선만 확인

공간 복잡도

O(H) - H는 트리/그래프의 높이(깊이)

•

재귀 호출 스택에 저장되는 최대 깊이

•

최악의 경우 (편향 트리): O(N)

•

최선의 경우 (균형 트리): O(log N)

•

visited 배열: O(V)

실전 예시:

7. 실전 문제 해결 팁

DFS 구현 체크리스트

트리 DFS를 구현할 때:

재귀 함수 정의 (현재 노드, 레벨)

현재 노드 처리 (출력/저장)

자식 노드들 순회

각 자식에 대해 재귀 호출

그래프 DFS를 구현할 때:

visited 배열 선언 및 초기화

시작 노드 방문 표시

재귀 함수 정의

인접 노드 중 미방문 노드만 탐색

방문 즉시 visited 표시 (중요!)

자주 하는 실수

실수 1: visited 표시 시점 잘못됨

// 잘못된 코드
run(i, level + 1);
visited[i] = 1;  // ❌ 재귀 후에 표시 → 중복 방문 발생!

// 올바른 코드
visited[i] = 1;  // ✅ 재귀 전에 표시
run(i, level + 1);
C++
복사

실수 2: 시작 노드 visited 표시 안 함

// 잘못된 코드
run(0, 0);  // ❌ visited[0] 표시 안 함 → 다시 방문 가능!

// 올바른 코드
visited[0] = 1;  // ✅ 시작 전에 표시
run(0, 0);
C++
복사

실수 3: 종료 조건 없음

// 잘못된 코드
void run(int now) {
    std::cout << tree[now];
    run(now * 2);  // ❌ 종료 조건 없음 → 무한 재귀!
}

// 올바른 코드
void run(int now) {
    if (tree[now] == '\0') return;  // ✅ 종료 조건
    std::cout << tree[now];
    run(now * 2);
}
C++
복사

디버깅 팁

출력으로 확인하기:

void run(int now, int level) {
    // 들여쓰기로 깊이 시각화
    for(int i = 0; i < level; i++) std::cout << "  ";
    std::cout << "방문: " << value[now] << " (깊이: " << level << ")\n";
    
    for (size_t i = 0; i < 5; i++) {
        if (map[now][i] == 1 && visited[i] == 0) {
            visited[i] = 1;
            run(i, level + 1);
        }
    }
}
C++
복사

출력 예시:

연습 문제 접근법

문제를 받았을 때:

트리인가, 그래프인가? → visited 배열 필요 여부 결정

무엇을 찾는가? → 경로? 특정 노드? 모든 노드?

어떻게 저장되어 있는가? → 인접 행렬? 리스트? 배열?

종료 조건은? → 리프 노드? 목표 발견? 모두 방문?

결과를 어떻게 저장? → 출력만? 경로 저장? 개수 세기?

“강의는 많은데, 왜 나는 아직도 코드를 못 짤까?”

혼자 공부하다 보면 누구나 이런 고민을 하게 됩니다.

•

강의는 다 들었지만 막상 손이 안 움직이고,

•

복습을 하려 해도 무엇을 다시 봐야 할지 모르겠고,

•

질문할 곳도 없고,

•

유튜브는 결국 정답을 따라 치는 것밖에 안 되는 것 같고.

문제는 ‘연습’이 빠졌기 때문입니다.

단순히 강의를 듣는 것만으로는 실력이 늘지 않습니다.

실제 문제를 풀고, 고민하고, 직접 구현해보는 시간이 반드시 필요합니다.

그래서, 얌얌코딩 코칭은 다릅니다.

그냥 가르치지 않습니다.

스스로 설계하고, 코딩할 수 있게 만듭니다.

얌얌코딩 코칭에서는 단순한 예제가 아닌,

스스로 문제를 분석하고 구현해야 하는 연습문제를 제공합니다.

이 연습문제들은 다음과 같은 역량을 키우기 위해 설계되어 있습니다:

•

문제를 스스로 쪼개고 설계하는 힘

•

다양한 조건을 만족시키는 실제 구현 능력

•

기능 단위가 아닌, 프로그램 단위로 사고하는 습관

•

마침내 자신의 힘으로 코드를 끝까지 작성하는 경험

지금 필요한 건 더 많은 강의가 아닙니다.

코드를 스스로 완성해 나가는 훈련,

그것이 지금 실력을 끌어올릴 가장 현실적인 방법입니다.

자세한 안내 보기: 프리미엄 코칭 안내 바로가기

또는 카카오톡 상담방: 얌얌코딩 상담방