LV02 기본기 복습(마스킹, 다중카운팅, 인덱스, 함수)

C++ 고급 배열 기법과 알고리즘

비트별로 마스킹 하기

마스킹(Masking)의 개념

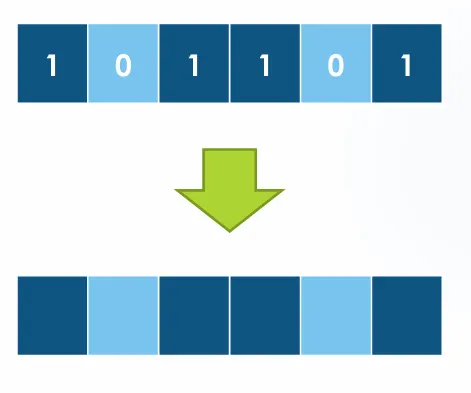
마스킹은 1과 0이 들어있는 배열을 단순하게 색칠해서 나타낼 수 있는 기법입니다. 내가 원하는 값만 뽑아내기 위해, 필요 없는 값을 필터에 거르는 작업을 뜻합니다.

마스킹 동작 원리

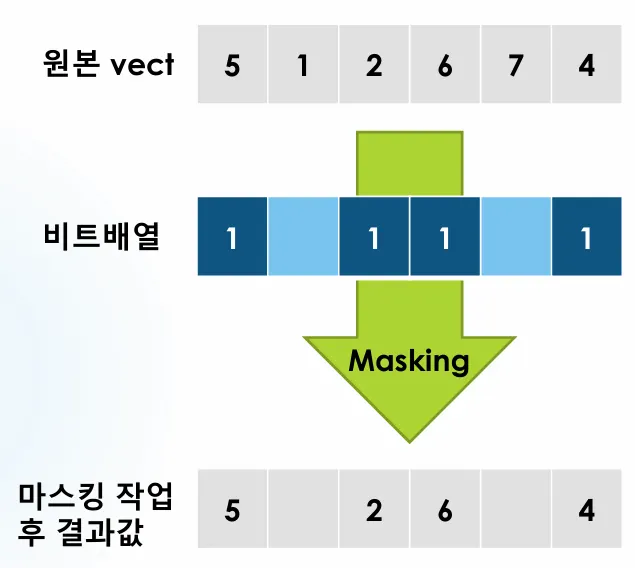
시각적 표현:

마스킹 과정:

마스크 배열: 1은 선택, 0은 제외를 의미

필터링: 마스크가 1인 위치의 값만 결과에 포함

결과 생성: 선택된 값들로 새로운 배열 생성

마스킹 구현

#include <iostream>
using namespace std;

int main()
{
    int mask[4] = { 1, 1, 0, 1 };
    int arr[4] = { 3, 7, 45, 8 };
    int ret[4] = { 0, 0, 0, 0 };

    for (size_t i = 0; i < 4; i++)
    {
        if (mask[i] == 1)
        {
            ret[i] = arr[i];
        }
    }

    // 결과 출력
    cout << "원본 배열: ";
    for (int i = 0; i < 4; i++)
    {
        cout << arr[i] << " ";
    }
    cout << endl;

    cout << "마스크 배열: ";
    for (int i = 0; i < 4; i++)
    {
        cout << mask[i] << " ";
    }
    cout << endl;

    cout << "결과 배열: ";
    for (int i = 0; i < 4; i++)
    {
        cout << ret[i] << " ";
    }
    cout << endl;

    return 0;
}
C++
복사

실행 결과:

원본 배열: 3 7 45 8
마스크 배열: 1 1 0 1
결과 배열: 3 7 0 8
Plain Text
복사

마스킹의 실용적 활용

이미지 처리에서의 마스킹:

•

특정 영역만 효과 적용

•

배경 제거 (크로마키)

•

관심 영역(ROI) 추출

데이터 분석에서의 마스킹:

•

조건에 맞는 데이터만 선택

•

이상치(outlier) 제거

•

특정 범위 값 필터링

다중 카운트

배열에서 각 원소의 개수 세기

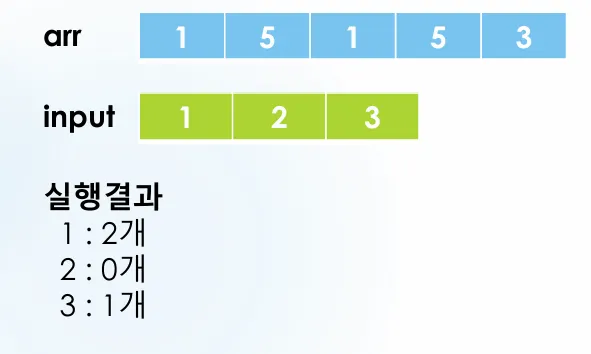
임의발은 숫자 배열에 몇개 있는지 count 하는 방법입니다. 각 값이 몇 번 나타나는지 효율적으로 계산하는 알고리즘입니다.

#include <iostream>
using namespace std;

int main()
{
    int arr[5] = { 1, 5, 1, 5, 3 };
    int input[3] = { 1, 2, 3 };

    for (size_t y = 0; y < 3; y++)
    {
        int count = 0;
        for (size_t x = 0; x < 5; x++)
        {
            if (arr[x] == input[y])
            {
                count++;
            }
        }
        cout << input[y] << ": " << count << "개" << endl;
    }

    return 0;
}
C++
복사

실행 결과:

1: 2개
2: 0개
3: 1개
Plain Text
복사

알고리즘 분석:

•

시간 복잡도: O(n×m) (n: 배열 크기, m: 찾을 값의 개수)

•

공간 복잡도: O(1) (추가 배열 불필요)

•

장점: 구현 간단, 이해하기 쉬움

•

단점: 많은 값을 찾을 때 비효율적

다중 flag

여러 조건을 동시에 확인하는 방법

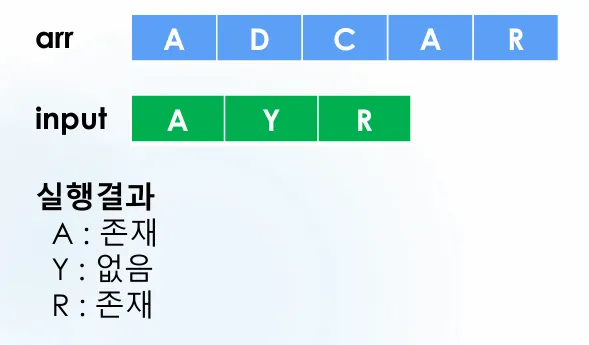
문자 3개를 입력받고, 입력받은 문자들이 arr배열에 각각 존재하는지 확인하는 방법입니다.

#include <iostream>
using namespace std;

int main()
{
    int arr[5] = { 1, 5, 1, 5, 3 };
    int input[3] = { 1, 2, 3 };

    for (size_t y = 0; y < 3; y++)
    {
        int flag = 0;
        for (size_t x = 0; x < 5; x++)
        {
            if (arr[x] == input[y])
            {
                flag = 1;
                break;  // 찾으면 즉시 중단 (효율성)
            }
        }

        if (flag == 1)
        {
            cout << "존재 O" << endl;
        }
        else
        {
            cout << "존재 X" << endl;
        }
    }

    return 0;
}
C++
복사

다중 플래그의 장점:

•

조기 종료: 찾으면 즉시 break로 반복 중단

•

메모리 효율: 각 검색마다 하나의 flag 변수만 사용

•

가독성: 존재 여부를 명확하게 표현

개선된 다중 플래그 (함수 활용):

다중 플래그 대신 함수를 만들어서 문제를 해결하면 조금 더 간결해서 가독성 좋게 해결이 가능합니다.

isExist 함수 사용

main함수에서는 1중 for문만 체크하고 있기 때문에 가독성도 좋고 코딩하기도 편하다.

#include <iostream>
using namespace std;

int arr[5] = { 1, 5, 1, 5, 3 };
int input[3] = { 1, 2, 3 };

int isExist(int data)
{
    for (size_t x = 0; x < 5; x++)
    {
        if (arr[x] == data)
        {
            return 1;  // 즉시 반환
        }
    }

    return 0;  // 찾지 못함
}

int main()
{
    for (size_t y = 0; y < 3; y++)
    {
        int flag = isExist(input[y]);

        if (flag == 1)
        {
            cout << "존재 O" << endl;
        }
        else
        {
            cout << "존재 X" << endl;
        }
    }

    return 0;
}
C++
복사

함수 활용의 장점:

•

코드 재사용: 다른 곳에서도 isExist 함수 활용 가능

•

가독성 향상: main 함수가 단순해짐

•

유지보수 용이: 검색 로직 변경 시 한 곳만 수정

•

테스트 편의: 함수 단위로 테스트 가능

앞으로 문제들을 할때는 최대한 함수로 나누고 싶다면 함수를 활용해 문제를 풀어야겠다.

Base 인덱스와 Offset의 개념

상대적 인덱싱 시스템

Base 인덱스는 기준 index를 말하고 offset 기준 index로부터 얼마큼 떨어져있는지를 나타냅니다.

배열에서의 Base와 Offset

Offset 계산 예시:

•

base index [b] 니가 찾고자하는 값은 다 → offset 2칸이다

•

base index [c] 니가 찾고자하는 값은 t → offset 6칸이다

•

base index [g] 니가 찾고자하는 값은 d 다 → offset -3칸이다

Offset의 특징:

•

양수: base보다 오른쪽에 위치

•

음수: base보다 왼쪽에 위치

•

0: base와 같은 위치

2차원 배열에서의 Offset

마찬가지로 2차원 배열 일때도 가능한 말이다.

2차원 Offset 예시:

•

base index (1, 1) → x축으로 +1, y축으로 +2 떨어진 값을 출력해라: 8 출력 (offset x:1, y:2)

2차원 Offset 공식:

int getValue(int baseY, int baseX, int offsetY, int offsetX)
{
    int targetY = baseY + offsetY;
    int targetX = baseX + offsetX;

    // 경계 검사
    if (targetY >= 0 && targetY < rows &&
        targetX >= 0 && targetX < cols)
    {
        return array[targetY][targetX];
    }

    return -1; // 범위 벗어남
}
C++
복사

getSum() 함수 만들기

부분 배열의 합 계산

index 1개를 입력받고 연속된 4개의 배열의 값들의 합을 출력해보자.

구현 및 활용

#include <iostream>
using namespace std;

int vect[9] = {4, 3, 5, 1, 7, 5, 6, 8, 2};

int getSum(int target)
{
    int sum = 0;
    for (int i = target; i < target + 4; i++)
    {
        sum += vect[i];
    }

    return sum;
}

int main()
{
    int idx = 0;
    cout << "시작 인덱스를 입력하세요: ";
    cin >> idx;

    int ret = getSum(idx);
    cout << "연속된 4개 원소의 합: " << ret << endl;

    return 0;
}
C++
복사

예시 실행:

시작 인덱스를 입력하세요: 1
연속된 4개 원소의 합: 16
// vect[1] + vect[2] + vect[3] + vect[4] = 3 + 5 + 1 + 7 = 16
Plain Text
복사

안전한 버전의 getSum 함수

int getSumSafe(int target, int length)
{
    // 경계 검사
    if (target < 0 || target + length > 9)
    {
        cout << "범위를 벗어났습니다!" << endl;
        return -1;
    }

    int sum = 0;
    for (int i = target; i < target + length; i++)
    {
        sum += vect[i];
    }

    return sum;
}
C++
복사

두 문자열 배열이 완전히 똑같은지 확인하는 방법

문자열 비교 함수 구현

1중for문을 돌려서 flag기법으로 단순하게 비교해도 좋지만 flag를 함수로 만들어서 사용해줘야 한다.

이제는 코드가 복잡해지고 점점 길어지고 로직도 많아지기 때문에 디버깅과 가독성을 편하게 가지고 가려면 함수로 묶어주는 습관을 꼭!!! 길러줘야한다.

#include <iostream>
using namespace std;

bool IsSame(char* strA, char* strB)
{
    for (int i = 0; i < 256; i++)
    {
        if (strA[i] != strB[i]) // 하나라도 다른데 값이 더이상 못부름을 체크할필요가 없다.
        {
            return false;
        }
    }

    return true;
}

int main()
{
    char strA[256] = "ABCD";
    char strB[256] = "ABCE";

    bool checkk = IsSame(strA, strB);

    if (checkk)
    {
        cout << "Same" << endl;
    }
    else
    {
        cout << "Different" << endl;
    }

    return 0;
}
C++
복사

개선된 문자열 비교 함수

bool IsSameImproved(char* strA, char* strB)
{
    int i = 0;

    // null 문자를 만날 때까지 비교
    while (strA[i] != '\0' && strB[i] != '\0')
    {
        if (strA[i] != strB[i])
        {
            return false;
        }
        i++;
    }

    // 길이가 다른 경우 체크 (한쪽이 먼저 끝남)
    return strA[i] == strB[i];
}
C++
복사

함수화의 중요성

함수 분리의 장점:

디버깅 편의: 문제 발생 시 함수 단위로 확인

가독성 향상: main 함수가 간결해짐

재사용성: 다른 곳에서도 활용 가능

테스트 용이: 개별 함수별 단위 테스트

유지보수: 로직 변경 시 한 곳만 수정

실무에서의 함수 설계 원칙:

•

단일 책임: 하나의 함수는 하나의 기능만

•

명확한 이름: 함수 이름으로 기능 파악 가능

•

적절한 크기: 한 화면에 들어올 정도의 길이

•

입출력 명확: 매개변수와 반환값의 의미 명확

실무 활용 예시

데이터 필터링 시스템

#include <iostream>
using namespace std;

class BitMaskFilter 
{
public:
    // 생성자
    BitMaskFilter(int* inputData, int dataSize) : mData(inputData), mSize(dataSize) 
    {
        mMask = 0xFFFFFFFF; // 모든 비트를 1로 설정 (모든 데이터 포함)
        if (mSize < 32) 
        {
            mMask = (1U << mSize) - 1; // size만큼의 비트만 1로 설정
        }
    }
    
    // 소멸자 (동적 할당이 없으므로 기본 소멸자 사용)
    ~BitMaskFilter() {}
    
    // 멤버 함수들
    
    // 특정 인덱스의 필터 설정
    void SetBit(int index, bool value) 
    {
        if (index >= 0 && index < mSize && index < 32) 
        {
            if (value) 
            {
                mMask |= (1U << index);  // 비트 설정
            }
            else 
            {
                mMask &= ~(1U << index); // 비트 해제
            }
        }
    }
    
    // 특정 인덱스의 필터 상태 확인
    bool GetBit(int index) 
    {
        if (index >= 0 && index < mSize && index < 32) 
        {
            return (mMask & (1U << index)) != 0;
        }
        return false;
    }
    
    // 마스크 전체 설정
    void SetMask(unsigned int newMask) 
    {
        mMask = newMask;
    }
    
    // 필터 적용
    int ApplyFilter(int* result) 
    {
        int resultIndex = 0;
        for (int i = 0; i < mSize && i < 32; i++) 
        {
            if (mMask & (1U << i)) // i번째 비트가 1인지 확인
            {
                result[resultIndex++] = mData[i];
            }
        }
        return resultIndex; // 결과 개수 반환
    }
    
    // 마스크 상태 출력 (디버깅용)
    void PrintMask() 
    {
        cout << "Mask (binary): ";
        for (int i = mSize - 1; i >= 0; i--) 
        {
            cout << ((mMask & (1U << i)) ? '1' : '0');
        }
        cout << " (0x";
        cout.flags(ios::hex);
        cout << mMask;
        cout.flags(ios::dec);
        cout << ")" << endl;
    }
    
    // 모든 비트 설정
    void SetAllBits() 
    {
        mMask = (mSize < 32) ? (1U << mSize) - 1 : 0xFFFFFFFF;
    }
    
    // 모든 비트 해제
    void ClearAllBits() 
    {
        mMask = 0;
    }
    
    // 마스크 반전
    void InvertMask() 
    {
        mMask = ~mMask;
        if (mSize < 32) 
        {
            mMask &= (1U << mSize) - 1; // 사용하지 않는 상위 비트 제거
        }
    }
    
    // 두 마스크의 교집합
    void IntersectWith(unsigned int otherMask) 
    {
        mMask &= otherMask;
    }
    
    // 두 마스크의 합집합
    void UnionWith(unsigned int otherMask) 
    {
        mMask |= otherMask;
    }
    
    // 설정된 비트 개수 세기 (Population Count)
    int CountSetBits() 
    {
        int count = 0;
        unsigned int temp = mMask;
        while (temp) 
        {
            count += temp & 1;
            temp >>= 1;
        }
        return count;
    }

private:
    // 멤버 변수들
    int* mData;              // 원본 데이터 배열
    unsigned int mMask;      // 32개의 플래그를 저장할 수 있는 비트 마스크
    int mSize;               // 데이터 배열의 크기
};

// 사용 예시
int main() 
{
    int data[] = {10, 20, 30, 40, 50, 60, 70, 80};
    int dataSize = 8;
    int result[8];
    
    BitMaskFilter filter(data, dataSize);
    
    cout << "=== 비트 마스킹 데이터 필터링 예제 ===" << endl << endl;
    
    // 초기 상태 (모든 데이터 포함)
    cout << "1. 초기 상태 (모든 데이터 포함):" << endl;
    filter.PrintMask();
    int count = filter.ApplyFilter(result);
    cout << "필터된 데이터: ";
    for (int i = 0; i < count; i++) 
    {
        cout << result[i] << " ";
    }
    cout << endl << endl;
    
    // 특정 인덱스만 선택 (0, 2, 4, 6번째)
    cout << "2. 짝수 인덱스만 선택 (0, 2, 4, 6):" << endl;
    filter.ClearAllBits();
    filter.SetBit(0, true);
    filter.SetBit(2, true);
    filter.SetBit(4, true);
    filter.SetBit(6, true);
    filter.PrintMask();
    count = filter.ApplyFilter(result);
    cout << "필터된 데이터: ";
    for (int i = 0; i < count; i++) 
    {
        cout << result[i] << " ";
    }
    cout << endl << endl;
    
    // 비트 연산으로 마스크 직접 설정
    cout << "3. 비트 연산으로 마스크 설정 (0b10110101):" << endl;
    filter.SetMask(0b10110101); // 0, 2, 4, 5, 7번째 비트 설정
    filter.PrintMask();
    count = filter.ApplyFilter(result);
    cout << "필터된 데이터: ";
    for (int i = 0; i < count; i++) 
    {
        cout << result[i] << " ";
    }
    cout << "설정된 비트 개수: " << filter.CountSetBits() << endl << endl;
    
    // 마스크 반전
    cout << "4. 마스크 반전:" << endl;
    filter.InvertMask();
    filter.PrintMask();
    count = filter.ApplyFilter(result);
    cout << "필터된 데이터: ";
    for (int i = 0; i < count; i++) 
    {
        cout << result[i] << " ";
    }
    cout << endl << endl;
    
    // 두 마스크의 교집합
    cout << "5. 마스크 교집합 연산:" << endl;
    filter.SetMask(0b11110000); // 상위 4비트
    cout << "마스크 A: ";
    filter.PrintMask();
    
    unsigned int maskB = 0b10101010; // 짝수 비트들
    cout << "마스크 B: ";
    for (int i = 7; i >= 0; i--) 
    {
        cout << ((maskB & (1U << i)) ? '1' : '0');
    }
    cout << endl;
    
    filter.IntersectWith(maskB);
    cout << "교집합 결과: ";
    filter.PrintMask();
    count = filter.ApplyFilter(result);
    cout << "필터된 데이터: ";
    for (int i = 0; i < count; i++) 
    {
        cout << result[i] << " ";
    }
    cout << endl;
    
    return 0;
}
C++
복사

이러한 고급 배열 기법들은 알고리즘 문제 해결, 게임 개발, 데이터 분석 등 다양한 분야에서 핵심적으로 활용됩니다.

안녕하세요,

야무지고 맛있게 코딩하는 얌얌코딩입니다!

단순히 영상을 보는 것만으로는 부족한 분들,

"직접 손으로 풀어보며 성장하고 싶다"는 분들을 위해

얌얌코딩 유튜브 멤버십 전용 혜택을 마련했습니다.

멤버십 전용 혜택

단계별 연습문제 & 복습문제 PDF 제공

→ 강의에서 배운 내용을 직접 연습하며 복습할 수 있어요!

디스코드 전용 채널 입장 가능

→ 질문, 피드백, 코드 리뷰, 실습 자료 공유까지

디스코드 서버 바로가기

선공개 자료 및 전용 코드 예제 제공

커리어, 포트폴리오 관련 Q&A/코멘트도 비정기적으로 제공

 얌얌코딩 숙제, 전용 자료실은 "학생얌얌이" 등급 이상부터 제공됩니다.

일반 멤버십(입문얌얌)은 접근이 제한되며,

연습문제 다운로드 및 디스코드 채널 열람은 "학생얌얌" 등급 이상이어야 가능합니다.

가입 방법

아래 링크 클릭하여 멤버십 가입

멤버십 가입하기

디스코드 서버 입장

디스코드 초대 링크

유튜브 계정과 디스코드 계정 연동

→ 자동으로 멤버 등급 확인 후, 전용 채널 열립니다

→ (문제 시 디스코드 내 안내 채널에서 도움 요청 가능)