힙(Heap) 자료구조 수업노트
힙(heap)이란?
힙은 완전 이진 트리의 일종인 자료구조
•
완전 이진 트리: 마지막 레벨을 제외한 모든 레벨의 자식들이 왼쪽부터 채워진 이진 트리
•
우선순위 큐를 위하여 만들어진 자료구조이며 개의 값들 중에서 최댓값/최솟값을 빠르게 찾아내도록 만들어짐
힙의 종류
•
최대 힙(max heap): 부모 노드의 키 값 >= 자식 노드의 키 값을 만족하는 완전 이진 트리
•
최소 힙(min heap): 부모 노드의 키 값 <= 자식 노드의 키 값을 만족하는 완전 이진 트리
•
느슨한 정렬 상태(반정렬 상태) 유지하지만 트리의 깊이 중복 값 허용
배열로 힙 구현하기
배열로 힙 구현하기는 완전 이진 트리이기 때문에 빈 공간이 없어 배열로 구현하기에 용이하다. 구현을 쉽게 하기 위해 배열의 인덱스는 1부터 사용하고, 주는 노드를 1번으로 저장하고 같은 레벨에서 좌에서 우로 저장하는 순서로 저장한다.
배열 힙 구현 인덱스 규칙
배열로 힙 구현
부모 노드 i
왼쪽 자식 노드 2i
오른쪽 자식 노드 2i + 1
Plain Text
복사
배열 인덱스: [0, 1, 2, 3, 4, 5, 6]힙 값: [-, 15, 12, 7, 5, 3, 6]
힙 제거과정(heapify)
힙 제거과정(heapify)함에서 원소의 삽입이나 삭제가 일어나면 최대 힙의 조건이 깨질 수 있다. 이 경우 다시 최대 힙의 조건을 만족하도록 노드의 위치를 바꾸는 것을 heapify라고 한다.
삽입과 삭제의 경우 연산 자체는 O(n)의 시간 복잡도로 작동하지만, heapify의 과정이 O(logN)이기 때문에 최종적으로O(logN)의 시간 복잡도를 가지게 된다.
최대 힙 삽입 과정
원소를 가장 맨 뒤 노드에 삽입한 다음, 가장 맨뒤 노드부터 부모 노드와 값을 비교하여 최대 힙 조건을 만족하지 않을때마다 위치를 바꿔준다.
삽입 과정 예시 (최대 20 삽입)
1.
가장 맨 뒤 노드에 원소 삽입 (최대 힙에 원소 20 삽입)
2.
부모 노드와 비교하여 값이 크면 교환, 작으면 정지 (20이 부모 노드 7보다 크기 때문에 교환)
3.
2번 과정을 반복 (20이 부모 노드 15보다 크기 때문에 교환)
최악의 경우 가장 말단에서 삽입한 원소가 루트 노드까지 올라가게 되므로, 이때의 비교 횟수는 트리의 높이만큼이다. 따라서 삽입의 경우 heapify의 시간 복잡도는O(logN)이 된다.
최대 힙 삭제 과정
가장 원소인 루트 노드를 삭제하고 나면, 가장 맨뒤의 원소를 루트로 이동시킨다. 이후 루트 노드부터 자식 노드와 비교하여 최대 힙 조건을 만족하도록 힙을 구성한다.
삭제 과정 예시
1.
루트 노드 삭제 후 가장 말단 노드를 루트 노드로 이동
2.
큰 값을 가진 자식과 위치 교환, 자식의 가장 크다면 정지
3.
2번의 과정을 반복 (자식 노드 6보다 7이 크므로 교환하지 않고 정지)
삽입 과정과 유사하게, 최악의 경우 루트 노드에서 말말 노드까지 내려오게 되므로 비교 횟수는 트리의 높이만큼이다. 따라서 삭제 과정에서 heapify의 시간 복잡도는O(logN)이 된다.
힙 만들기(build heap)
build heap은 임의 아닌 배열을 힙으로 만드는 과정이다. 이때 heapify를 N번 진행하게 되므로 시간 복잡도는 O(NlogN)이다.
build heap 과정
가장 맨뒤의 오른쪽에 있는 노드의 부모 노드부터 위에서 아래로 heapify를 진행한다.
과정 예시: 10, 3, 5, 8, 7, 12 → heapify 과정을 통해 최대 힙으로 변환
최소 힙 삽입상세 예제
C++ 구현 코드
#include <iostream>
#include <queue>
int heap[256] = {};
int hn = 0;
void push(int value)
{
heap[++hn] = value;
int now = hn;
int parent = 0;
while (true)
{
// 부모의 index = 자식의 나누기 2
parent = now / 2;
// now가 root이면 부모가 없기 때문에 다이상 swap할 필요가 없다.
if (now == 1)
break;
// now가 부모보다 킬거나 클 경우 더 이상 swap할 필요가 없다.
if (heap[parent] <= heap[now])
break;
std::swap(heap[parent], heap[now]);
now = parent;
}
}
int pop()
{
int backup = heap[1];
heap[1] = heap[hn];
heap[hn--] = 0;
int now = 1;
int son = 0;
while (true)
{
// 왼쪽 자식
son = now * 2;
//왼쪽자식과 오른쪽 자식중에 더 작은 값을 설택 (둘째가 없으면 선택하지 않음)
if (son + 1 <= hn && heap[son] > heap[son+1])
{
son++;
}
// 자식이 없거나, 자식이 부모다 크거나 같으면 다이상 swap할 필요가 없다.
if (son > hn || heap[son] >= heap[now])
break;
std::swap(heap[son], heap[now]);
now = son;
}
return backup;
}
int main()
{
//Heap 자료구조
//std::priority_queue<int> pq;
push(3);
push(5);
push(2);
push(4);
push(1);
push(6);
std::cout << pop() << std::endl;
std::cout << pop() << std::endl;
std::cout << pop() << std::endl;
std::cout << pop() << std::endl;
std::cout << pop() << std::endl;
std::cout << pop() << std::endl;
return 0;
}
C++
복사
힙의 특징 및 활용
시간 복잡도
•
삽입(push): O(log N)
•
삭제(pop): O(log N)
•
힙 생성(build heap): O(N log N)
공간 복잡도
•
배열 기반: O(N)
주요 활용 분야
•
우선순위 큐 구현
•
힙 정렬 알고리즘
•
최단 경로 알고리즘 (다익스트라)
•
허프만 코딩 등
C++ STL
// 최대 힙 (기본)
std::priority_queue<int> max_heap;
// 최소 힙
std::priority_queue<int, std::vector<int>, std::greater<int>> min_heap;
C++
복사
핵심 포인트
1.
완전 이진 트리: 배열로 구현하기 용이
2.
느슨한 정렬: 완전 정렬이 아닌 부분 정렬 상태
3.
heapify 과정: 힙 속성 유지를 위한 핵심 연산
4.
O(log N) 성능: 삽입/삭제의 효율적인 시간 복잡도
5.
인덱스 규칙: 부모(i), 왼쪽 자식(2i), 오른쪽 자식(2i+1)
이진탐색이란?
이진 탐색이란 정렬돼 있는 데이터에서 특정한 값을 찾아내는 알고리즘이다.
•
이진탐색은 이분탐색이라고도 불린다. 이진탐색은 탐색 범위를 반으로 나누어 찾는 값을 포함하는 범위를 좁혀가는 방식으로 동작한다. 주로 배열의 인덱스를 기준으로 배열 내의 값을 탐색하는데 사용되지만, 리스트, 트리 등에서도 사용할 수 있다.
•
하지만 모든 리스트, 트리에서 사용할 수 있는 것이 아니라 반드시 원소들이 일정한 순서(예를 들면 오름차순)로 정렬된 구조에서만 사용할 수 있기 때문에 정렬된 리스트나 트리에서 사용이 가능하다.•
이진탐색의 시간 복잡도는 O(log n)으로, 배열의 크기에 비례하여 실행 시간이 빨라진다.
따라서 대용량 데이터에서 특정 값의 위치를 찾는 데 용이하다.
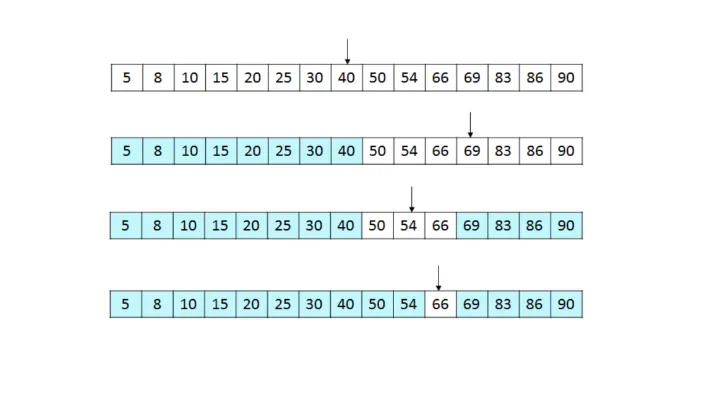
이진탐색의 동작 방식
이진 탐색의 동작 방식은 우리가 생각하는 중간점 탐색소거 방식과 크게 다르지 않다.
배열에서의 동작방식
1.
정렬된 배열에서 중간 인덱스(mid)를 찾는다.
2.
찾으려는 값(target)과 중간 값(mid_val)을 비교한다.
3.
target이 mid_val보다 작으면 mid를 기준으로 왼쪽 부분 배열을 탐색한다.target이 mid_val보다 크면 mid를 기준으로 오른쪽 부분 배열을 탐색한다.
4.
탐색 범위를 반으로 줄인다.
5.
탐색 범위가 더 이상 없을 때까지 위 과정을 반복한다.
예제 코드
#include <iostream>
#include <iostream>
#include <queue>
//binary search
int vect[10] = { 1, 2, 3, 4, 5, 6, 7, 9 };
int target = 7;
void runrecursive(int start, int end)
{
int mid = (start + end) / 2;
if (vect[mid] == target)
{
std::cout << "found" << std::endl;
return;
}
else if (vect[mid] < target)
{
runrecursive(mid + 1, end);
}
else
{
runrecursive(start, mid - 1);
}
}
void run()
{
while (true)
{
int start = 0;
int end = 7;
int mid = (start + end) / 2;
bool flag = false;
while (start <= end)
{
mid = (start + end) / 2;
if (vect[mid] == target)
{
flag = true;
std::cout << "found" << std::endl;
break;
}
else if (vect[mid] < target)
{
start = mid + 1;
}
else
{
end = mid - 1;
}
}
if (flag)
{
break;
}
if (start > end)
{
std::cout << "not found" << std::endl;
}
}
}
int main()
{
run();
//runrecursive(0, 7);
return 0;
}
JavaScript
복사
“강의는 많은데, 왜 나는 아직도 코드를 못 짤까?”
혼자 공부하다 보면 누구나 이런 고민을 하게 됩니다.
•
강의는 다 들었지만 막상 손이 안 움직이고,
•
복습을 하려 해도 무엇을 다시 봐야 할지 모르겠고,
•
질문할 곳도 없고,
•
유튜브는 결국 정답을 따라 치는 것밖에 안 되는 것 같고.
문제는 ‘연습’이 빠졌기 때문입니다.
단순히 강의를 듣는 것만으로는 실력이 늘지 않습니다.
실제 문제를 풀고, 고민하고, 직접 구현해보는 시간이 반드시 필요합니다.
그래서, 얌얌코딩 코칭은 다릅니다.
그냥 가르치지 않습니다.
스스로 설계하고, 코딩할 수 있게 만듭니다.
얌얌코딩 코칭에서는 단순한 예제가 아닌,
스스로 문제를 분석하고 구현해야 하는 연습문제를 제공합니다.
이 연습문제들은 다음과 같은 역량을 키우기 위해 설계되어 있습니다:
•
문제를 스스로 쪼개고 설계하는 힘
•
다양한 조건을 만족시키는 실제 구현 능력
•
기능 단위가 아닌, 프로그램 단위로 사고하는 습관
•
마침내 자신의 힘으로 코드를 끝까지 작성하는 경험
지금 필요한 건 더 많은 강의가 아닙니다.
코드를 스스로 완성해 나가는 훈련,
그것이 지금 실력을 끌어올릴 가장 현실적인 방법입니다.
자세한 안내 보기: 프리미엄 코칭 안내 바로가기 또는 카카오톡 상담방: 얌얌코딩 상담방