1. 서론(Introduction)
이 문서는 2012년 SIGGRAPH Asia를 위해 준비된 물리 기반 렌더링(Physically-Based Rendering, PBR)의 기초 개념에 관한 노트입니다.
첫 번째 저자가 컴퓨터 그래픽스를 시작했을 당시에는 지금처럼 인터넷이 발달하지 않았습니다. 엔지니어링은 소비 지출이 아니라 냉전 자금으로 지원되었고, 레이 트레이싱을 실행하는 데 며칠 혹은 몇 주가 걸리곤 했습니다. SIGGRAPH 강의 노트 또한 지금과는 달랐습니다. 당시 강의 노트는 렌더링과 관련된 실질적인 정보를 이해할 수 있는 거의 유일한 자료였습니다.
오늘날에는 훌륭한 책들이 많아졌고(그중 상당수는 SIGGRAPH 강의 노트에서 발전한 것들), 수백 개의 알찬 웹페이지와 수천 개의 질 낮은 웹페이지들이 존재합니다. 문제는 정보가 부족한 것이 아니라, 질적으로 들쭉날쭉한 정보가 너무 많다는 것입니다. 따라서 이 강의 노트는 또 하나의 세부적인 논의 자료가 아니라, 방대한 문헌 속에서 길잡이 역할을 하도록 작성되었습니다.
우선, 거의 모든 렌더링 연구자들이 이해하고 있지만 드물게 논의되는 중요한 문제가 하나 있습니다. 물리 기반 렌더링은 크게 세 가지 전혀 다른 목표 중 하나를 지향하며, 목표에 따라 접근 방식도 매우 달라집니다:
•
Predictive Rendering
실제로 장면을 제작했을 때의 결과와 반드시 일치해야 합니다. 주로 설계 및 시뮬레이션 애플리케이션에서 사용됩니다.
•
Plausible Rendering
결과가 충분히 그럴듯하게 보여야 하지만, 실제와 다를 수도 있습니다. 엔터테인먼트나 시각화 분야에서 주로 사용됩니다.
•
Visually Rich Rendering
현실의 시각적 풍부함을 필요로 하지만, 강하게 스타일화될 수도 있습니다.
이 노트에서는 주로 Predictive 렌더링에 집중합니다. 여기서 알고리즘보다는 주로 물리학과 수학을 의미합니다.
Predictive 렌더링이 다른 두 가지보다 더 중요하거나 우월한 것은 아닙니다. 하지만 마치 화가가 규칙을 깨기 전에 먼저 사실적인 드로잉을 배우는 것처럼, Predictive 접근을 배우는 것은 기초를 단단히 다지는 과정이며 이후 스타일화된 기법을 이해하는 데에도 도움이 됩니다.
2. Reading
시중에는 렌더링 관련 서적이 많이 있습니다. 렌더링을 직업으로 삼을 생각이 있다면 모두 구입하세요. 가장 최근의 책인 Physically Based Rendering 책으로 시작하면 좋습니다. 해당 책은 무료로 풀려 있으니 종이책이 필요하면 구매하여도 좋지만 한국에서는 3판까지밖에 번역이 되어 있지 않습니다. 4판부터 새롭게 추가된 내용(GPU 연산 활용)이 많습니다. 될 수 있다면 영어판으로 보는걸 추천합니다.
또한 Google Scholar와 같은 사이트 덕분에 예전보다 훨씬 쉬워졌습니다. Scholar의 핵심 기능은 논문을 참조한 모든 논문을 보여준다는 것입니다. 따라서 문헌 조사를 통해 시간 순으로 쉽게 진행할 수 있습니다. 또한 인용 횟수를 제공하여 모든 사람이 무엇을 읽고 있는지에 대한 좋은 아이디어를 얻을 수 있습니다. 다른 사람이 읽지 않는 좋은 논문을 읽음으로써 지식에서 우위를 점할 수 있지만, 문화적으로 이해하고 "큰" 논문을 읽는 것이 좋습니다.
3. Light
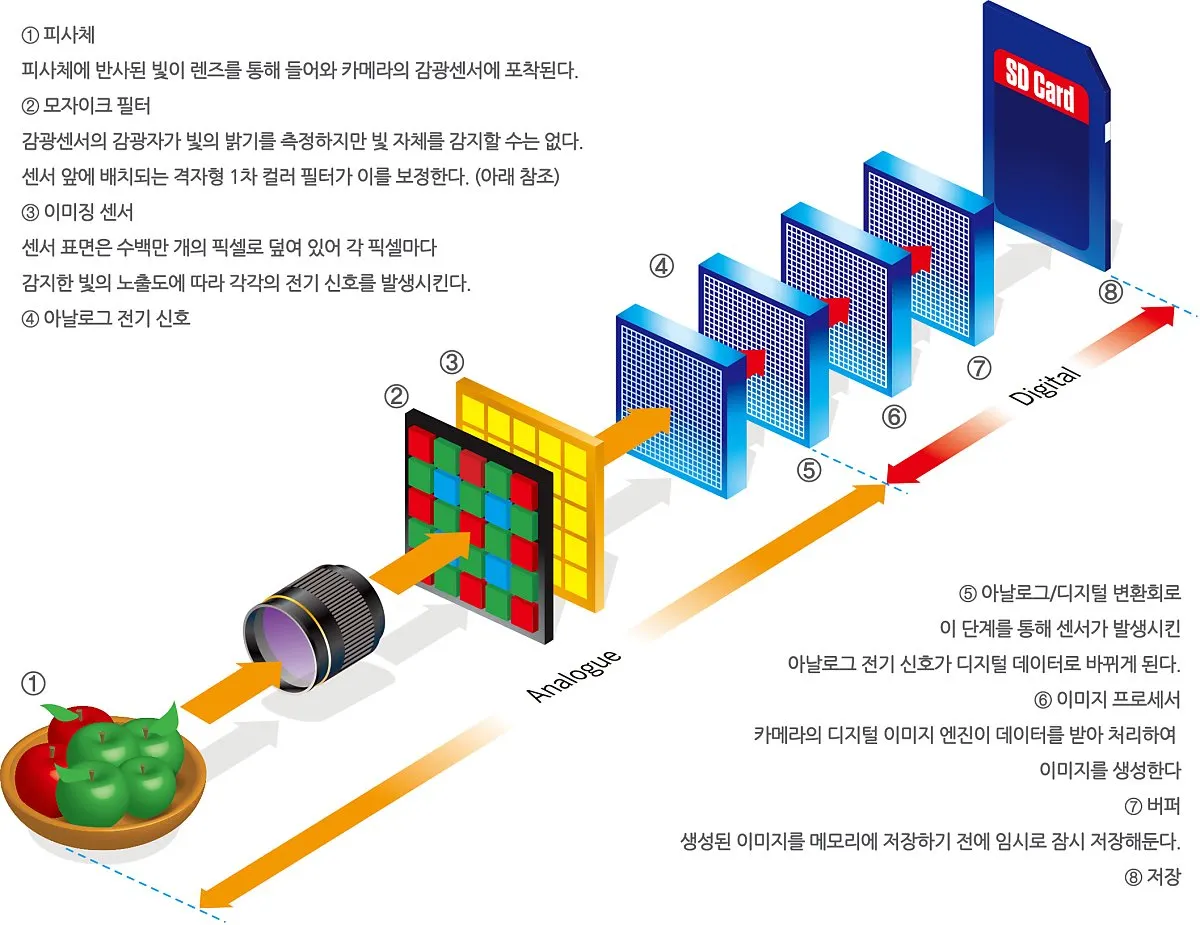
그래픽에서 우리는 일반적으로 카메라를 매우 간단하게 모델링합니다. 대부분의 응용 프로그램은 특정 사진이 사실적으로 보이는지 보다 "비사실적 이더라도 이쁘게 보이는지"에 더 중점을 두기 때문입니다. 이것이 우리가 찾는 이상적인 카메라 입니다.
아이러니하게도 카메라 불완벽함은 이미지를 오히려 비현실적으로 보이게 할 수 있습니다. 우리는 실제 카메라의 불완벽함 이미지에 익숙하기 때문입니다. 카메라는 일반적으로 렌즈 시스템과 센서로 구성됩니다. 센서는 픽셀이라 불리는 센서 요소들로 구성되어 있습니다. 각 픽셀은 빛의 방향과 파장에 따라 다르게 반응합니다.
이는 실시간 렌더링의 핵심 문제, 즉 '빛을 어떻게 개념화하고 측정할 것인가'라는 질문으로 귀결됩니다.
이 문제를 다루는 정석적인 접근 방식은 '복사측정법(Radiometry)'입니다. 복사측정법은 빛을 길이(m)나 질량(kg)처럼 정량적으로 다루는 물리적 체계입니다. 하지만 개발자들은 이 복사측정법을 일종의 '필요악'으로 간주합니다.
우리는 가능하면 이 복잡한 물리 이론을 피하려고 하며, 어쩔 수 없이 사용하게 될 때조차 그 세부 원리를 완벽하게 이해하지는 못하는 경우가 많습니다.
반면, 우리가 훨씬 더 직관적으로 받아들이고 잘 이해하는 개념은 '광자(photon)', 혹은 '광자 유사 입자'라 불리는 것입니다. 여기서 분명히 해야 할 점은, 그래픽스 전문가들이 '광자'라고 말할 때, 그것이 양자역학의 난해한 파동-입자 묶음을 의미하는 경우는 거의 없다는 것입니다.
여기서 말하는 '광자'란, 특정 파장(또S는 파장대)에서 일정량의 에너지를 운반하는 '아주 작은 구슬(ball-bearing)'과 같은 에너지 묶음(packet)을 의미합니다. 이는 물리학에서 때때로 '빛의 입자 모델'이라고 부르는 개념과 유사합니다.
이 글의 나머지 부분에서는 그래픽스 모델의 '광자'가 다음과 같은 속성을 갖는다고 가정하겠습니다.
•
단일한 파장
•
일정한 양의 에너지
•
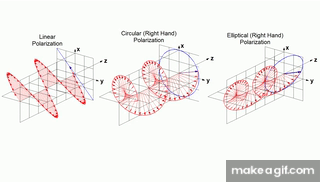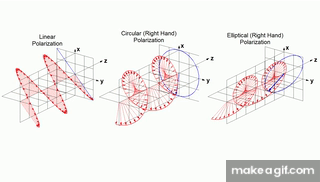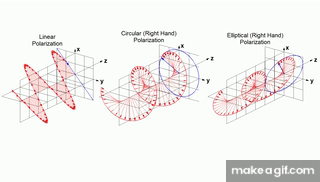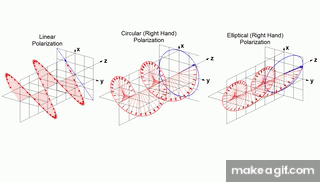
(경우에 따라) 선형 편광(linear polarization)
•
특정 시점의 위치와 진행 방향
다시 한번 강조하지만, 이것은 실제 광자를 극도로 단순화한 모델입니다.
심지어 이 모델의 '광자' 하나는 (시뮬레이션 효율을 위해) 수많은 실제 광자 묶음을 대표할 수 있으므로, 물리적인 실제 광자 하나보다 훨씬 더 큰 에너지를 운반하는 것으로 설정될 수 있습니다.
따라서 '광자'라고 부르기보다는 '입자(particle)'나 '에너지 구슬'이라고 부르는 것이 더 정확할 것입니다. 지금 다루는 이 개념이 물리학에서 말하는 본래의 광자(photon)와는 완전히 다른, 그래픽스 계산을 위한 편의상의 모델임을 반드시 기억해야 합니다.
3.1 Radiance
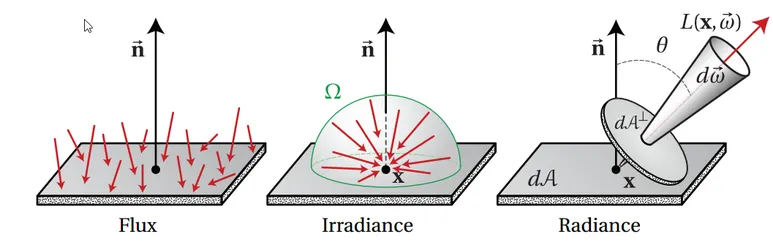
잎서위 그림을 보고 각 용어의 의미를 먼저 파악하겠습니다. Flux와 Irradiance, Radiance의 개념을 잘 설명해줍니다. Flux는 해당 면으로 들어오는 전자기 복사량, Irradiance는 모든 방향에서 단위 면적으로 입사하는 복사량, radiance는 한 지점에서 특정 방향으로의 투영면적당, 단위 입체각당 복사량 이라고 정리할 수 있습니다. Flux (선속)이라 함은 공간에서의 시간에 따른 물리적 값의 흐름을 뜻합니다. (위키피디아) flux 역시 에너지 개념으로 생각하면 일정 시간, 공간을 통과하는 에너지의 흐름 정도로 이해하고 넘어갑시다.
이제 **복사측정법(Radiometry)**에 대해 이야기해 보겠습니다. 이 개념은 기본적으로, 무한히 작은 에너지를 가진 수많은 광자(Photon)들을 하나로 모아, 거대하고 연속적인 함수인 것처럼 다루는 접근 방식입니다.
이때 모든 공간, 방향, 시간, 파장에 걸쳐 빛의 밀도 필드를 정의한 것을 **'복사 휘도(Radiance)'**라고 부릅니다. 더 정확한 기술 용어는 '스펙트럼 복사 휘도(Spectral Radiance)'지만, 실제로는 '스펙트럼'이라는 말을 거의 붙이지 않고 그냥 '복사 휘도'라고 통칭합니다.
모든 지점에서의 복사 휘도를 정의하는 이 함수는 종종 **'플레놉틱 함수(Plenoptic Function)'**라고도 불립니다. (때로는 여기에 '선형 편광'이나 '위상'을 포함한 '완전 편광(fully polarized light)'이 차원으로 추가되기도 합니다.)
솔직히 말해, 문헌에는 (우리 저자들이 작성한 것을 포함해서) 복사 휘도에 대한 수많은 논의가 있지만, 대부분이 꽤 혼란스럽습니다.
대신, 우리는 복사 휘도의 특성 중 실용적으로 유용한 네 가지 핵심 사항을 강조하고자 합니다.
1.
복사 휘도는 (매질이 없는) 빈 공간의 선을 따라 이동하는 동안 그 값이 일정하게 유지됩니다.
2.
복사 휘도는 우리가 특정 방향에서 인지하는 **'색상'과 '밝기'**라는 직관적인 개념과 매우 유사합니다.
3.
카메라나 눈과 같은 센서는 복사 휘도의 특정 지점 값이 아닌, 일정 영역과 각도에 대한 **모멘트(적분값)**를 측정합니다.
4.
다른 모든 복사측정량(예: 복사속, 조도)은 이 복사 휘도로부터 파생(적분)되어 계산될 수 있습니다.
1번과 2번 항목은 서로 관련이 있습니다. 광자는 이동하면서 에너지를 잃지 않으므로, 복사 휘도에는 '거리의 역제곱 법칙(inverse square rule)'이 적용되지 않습니다. 이 특성은 렌더링 코드를 작성할 때 복사 휘도를 다루기 매우 편리하게 만듭니다.
3번과 4번 항목도 마찬가지로 관련이 깊습니다. 대부분의 복사측정량 자체가 복사 휘도의 모멘트(특정 방식으로 적분한 값)이기 때문입니다.
복사 휘도를 공간을 정의하는 함수로 표현하고 싶다면, 아마도 다음과 같은 형태가 될 것입니다.
여기서 기호 은 스펙트럼 복사 휘도를 나타냅니다. 이 표기법()은 여러 분야에서 반쯤 표준처럼 쓰이는데, 그 이유는 복사 휘도(Radiance)가 인간의 시각을 고려한 측광 휘도(Photometric Luminance)와 사촌 관계에 있으며, 역사적으로 이 보편적인 선택지가 되었기 때문입니다.
이 함수에 대해 혼란스러운 점은, 이 함수가 반사(reflection)나 굴절(refraction)이 일어나는 '표면(surface)'을 제외한 모든 빈 공간에서는 매우 잘 정의된다는 것입니다.
이러한 이유로, 우리는 '표면'에서 일어나는 현상을 다룰 때 두 가지 종류의 복사 휘도를 구분합니다.
•
입사 복사 휘도 (Incoming Radiance): '필드 복사 휘도(Field Radiance)'라고도 합니다. 만약 어떤 표면 위에 작은 곤충이 앉아있다고 상상한다면, 그 곤충이 주변 환경(Environment Map처럼)으로부터 '표면으로 들어오는' 빛을 보는 것입니다.
•
출사 복사 휘도 (Outgoing Radiance): '표면 복사 휘도(Surface Radiance)'라고도 합니다. 관찰자가 그 표면을 바라볼 때, 표면에서 반사되거나 스스로 방출되어 '표면을 떠나 나가는' 빛을 보는 것입니다.
3.2 Moment Radiance
방사측정(radiometric)에는 여러 유용한 양이 있습니다. 이러한 양은 대부분 복사 휘도의 모멘트입니다. 즉, 복사 휘도에 상수나 함수를 곱한 후 적분한 값입니다.
가장 흔한 예는 **조사도(irradiance)**입니다. 조사도(irradiance)는 점 x에서 표면에 닿는 모든 방향에서 들어오는 빛의 밀도를 나타내며, 보통 H로 표기됩니다.
여기서 적분은 들어오는 방향 ω에 대한 것이고, θ는 표면 법선과 ω 사이의 각도입니다.
이와 유사하게, 나가는 방향에 대한 적분으로 계산되는 양이 **복사 발산도(radiant exitance)**입니다.
논문을 읽다 보면 조사도(irradiance)의 개념을 알아야 할 때가 있습니다. 하지만 실제로는 조사도를 직접 사용할 필요가 거의 없으며, 사용하더라도 복사 휘도의 적분으로 이해하는 것이 더 명확합니다.
3.3 Lambertian Surfaces
많은 표면은 무광택입니다. 이러한 표면은 그래픽을 비롯한 여러 분야에서 일반적으로 Lambertian 표면으로 근사됩니다. Lambertian 표면은 열역학적으로는 불가능하지만, 계산과 개념 면에서 편리하며 실제 무광택 표면과 매우 유사하게 보입니다.
Lambertian 표면의 기본 속성은 다음과 같습니다. 복사 휘도는 단위 면적당 닿는 빛의 총량에 선형적으로 비례하며, 모든 시야 방향에서 동일합니다.
표면에서 빛이 여러 번 반사되면서 표면이 빛을 사방으로 흩뿌리기 때문에 모든 시야 방향에서 동일합니다.
눈에 보이는 밝기는 [표면색] x [받은 빛]이 전부가 아닙니다. 이걸 로 나눠야 진짜 밝기가 됩니다. 는 에너지 보존을 위해 필요하지만, 많은 혼란과 버그를 일으키는 원인입니다.
"무광 표면이 받은 빛(피자 한판)을 모든 방향으로 흩뿌릴 때, 우리 눈(한 방향)에는 로 나눈 만큼(피자 한 조각)만 보입니다. 이게 에너지 보존의 핵심입니다.”
3.4 Weighted averages of radiance
모든 것을 '정규화된 휘도 모멘트(normalized moments of radiance)'로 공식화하면, ' 문제'와 복잡한 방사측정(radiometry) 분야를 우회할 수 있습니다.
이는 휘도의 가중 평균입니다. 한 지점에서의 정규화된 모멘트 는 다음과 같습니다.
이때 다음과 같은 정규화 제약(normalization constraint)이 적용됩니다.
이 를 정규화 항(normalization term)에 포함시켜 제거할 수 있습니다.
그러면 확산 표면(diffuse surface)의 휘도는 다음과 같습니다.
참고: 위치 는 암시적으로 포함되어 있어, 편의상 종종 생략됩니다.
결론
4. Rendering equation
렌더링 방정식은 1986년 Kajiya [7]와 Immel et al. [4]의 독립적인 논문을 통해 그래픽스 커뮤니티에 소개되었습니다. 이 방정식은 표면의 복사 휘도(radiance)를 입사하는 복사 휘도(radiance)와 연결합니다. 람다와 점을 생략하면 다음과 같은 형태입니다.
이 방정식의 의미는 간단합니다. 빛이 모든 방향에서 들어와 흡수되거나 방향이 바뀝니다. BRDF(양방향 반사 분포 함수) ρ는 표면 속성에 따라 달라집니다. 여기서 i와 o는 각각 들어오는 방향과 나가는 방향(필드 및 표면 복사 휘도에 해당)이며, L_e는 전구처럼 표면에서 직접 방출되는 빛입니다.
4.1 BRDF
그렇다면 BRDF 함수는 무엇일까요? 예를 들어, Lambertian 표면의 경우는 어떨까요?
이전 방정식에서 임을 알 수 있었습니다. 는 피할 수 없는 존재입니다. BRDF는 가중 모멘트를 만듭니다.
문헌에는 수십 개의 BRDF가 있으며, 거의 모든 BRDF가 난반사 항과 정반사 하이라이트 항으로 구성되어 있습니다.
대부분은 가 90도에 가까워질수록 정반사가 커지고 난반사가 작아지는 "프레넬 효과"를 나타냅니다.
어떤 모델이 더 뛰어난지는 중요하지 않습니다. Ward 모델이 좋은 선택이지만, 개선된 최신 버전 [2]을 사용하는 것이 좋습니다.
4.2 Variants of the rendering equation
렌더링 방정식은 여러 형태로 쓰여져 있습니다. 이러한 차이는 모두 표기법상의 차이일뿐 본질적으론 같습니다. 예를 들어 , Arvo [1]는 코사인을 측정값(즉, 투영된 면적 측정값)에 포함시키고 복사휘도를 "f"라고 부르는 것을 선호했는데, 이는 다음을 산출합니다.
이조차 복잡하다고 여겨 다음과 같은 방식을 선호했습니다.
또 다른 방정식은 방향이 아닌 표면()에 대해 적분하기 위해 변수를 다음과 같이 바꾸었습니다.
다음 방정식은 우리가 보는 표면이 우리와 관련하여 만드는 각도이고, dA는 표면의 넓이이며, 다음과 같이 표현도 가능합니다.
핵심은 적분이 모든 표면에 걸쳐 이루어진다는 점이며, 이 방식이 더 유용할 때가 많습니다.
렌더링 방정식은 함수가 자기 자신의 적분으로 정의되는 적분 방정식입니다. 하지만 많은 최신 알고리즘은 경로에 대한 적분 형태로 방정식을 다루기 때문에 재귀적이지 않습니다.
4.3 Reversability
렌더링 방정식의 핵심 특징은 자기 수반(self-adjoint)이라는 것입니다. 이는 빛의 방향을 뒤집을 수 있다는 의미에서 가역적입니다. 경로 추적기(path tracer)와 광자 추적기(photon tracer)는 본질적으로 동일합니다. 이것이 BRDF 공식이 유용한 이유 중 하나입니다. BRDF는 입사 방향과 출사 방향의 순서를 바꿔도 결과가 같다는 의미에서 상호적(reciprocal)입니다. 이 특성은 실제 세계에서 흥미로운 의미를 갖습니다 [11].
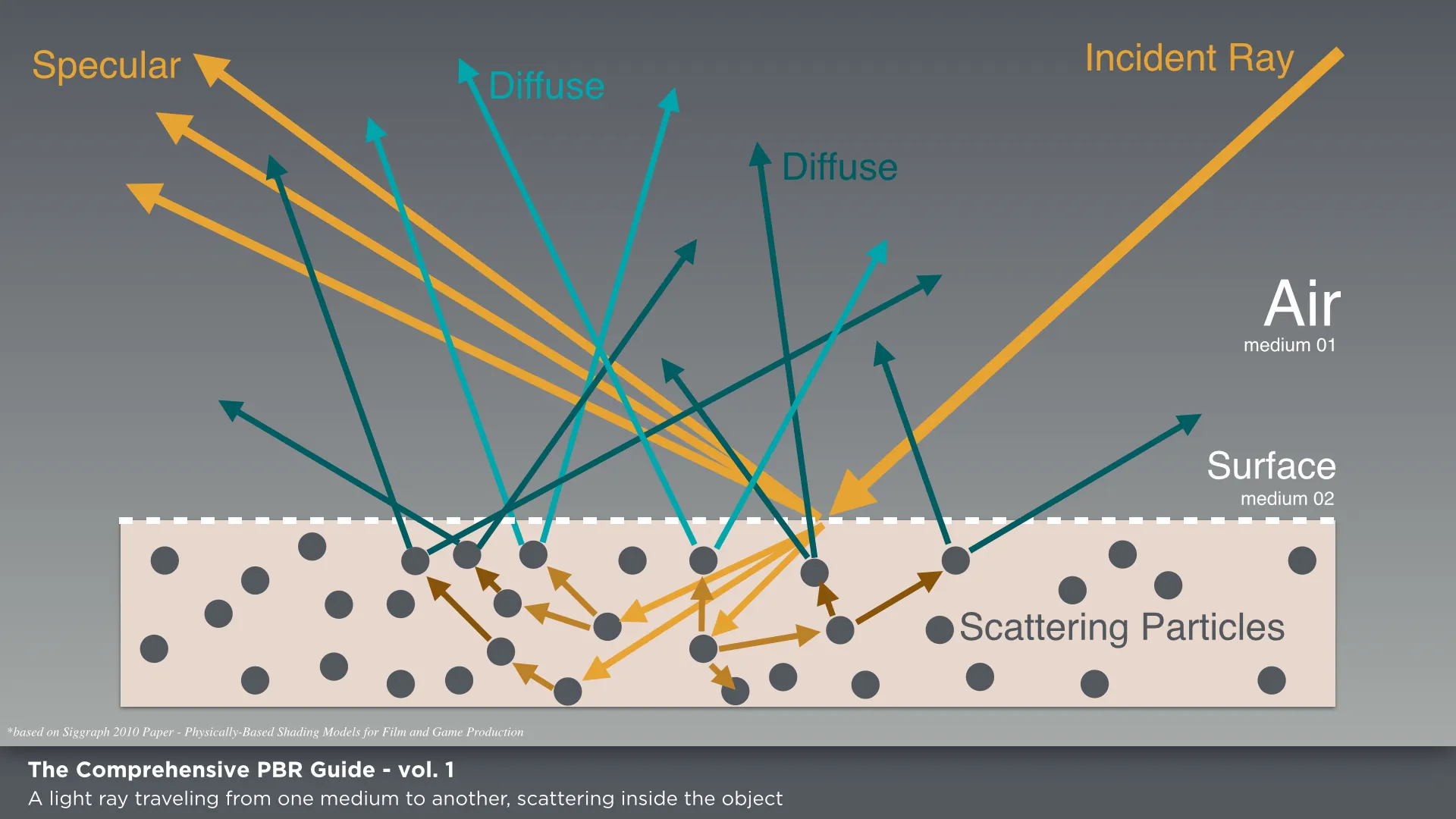
5. Smoke and fog
앞에서는 우리는 표면에 대해 논의 했습니다. 그러나 이 렌더링 방식은 연기나 안개에는 적용되지 않습니다. 핵심은 빛이 표면에서만 산란된다는 것이 아니라 광선을 따라 어느 곳에서나 산란될 수 있다는 것입니다. BRDF는 이를 지원해주지 않습니다. 대신 위상함수 는 볼륨내의 빛의 산란을 설명합니다.
광자 해석은 이를 직관적으로 만들어줍니다. 빛을 따라가면 광자가 입자에 부딪혀 흡수되거나, 산란될 작은 확률이 있습니다. 짧은 거리에서 부딪힐 확률 은 다음과 같습니다.
여기서 는 입자 밀도에 비례하며, 파장에 따라 달라질 수 있습니다. 예를 들어, 공기의 경우 이며, 이것이 하늘이 파란 이유입니다. 상호 작용이 발생하면 빛은 확률 로 산란됩니다. 이 는 여러 이름으로 불리지만, 기본적으로 반사율 또는 알베도입니다. 석탄 먼지는 0에 가깝고, 증기는 1에 가깝습니다. 이 값 역시 파장에 따라 달라집니다.
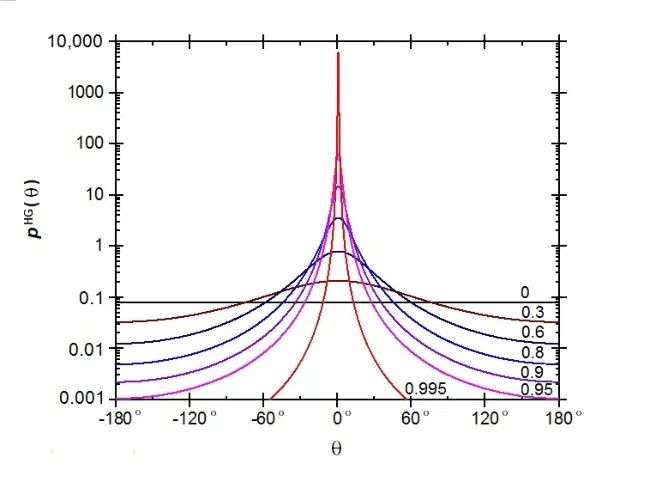
빛이 입자와 상호 작용하고 흡수되지 않으면 산란됩니다. 산란 방향은 (일반적으로 정규화된) 위상 함수 에 비례하는 분포를 따릅니다. 실제로는 등방성 상수 또는 Phong lighting model과 유사한 Henyey-Greenstein 함수가 널리 사용됩니다. 이는 편리하게 조정할 수 있는 함수입니다.
henyey greenstein scattering function
6. Camera and luminaries
카메라 모델은 매우 현실적이고 정교할 수 있지만, 실무에서는 종종 간소화됩니다. 우리는 일반적으로 특정 카메라 모델보다는 "사람이 보는 방식"을 원하며, 여기에 일부 렌즈 효과를 추가하는 정도입니다. 장면의 전체 밝기 정보를 유지하기 위해 삼자극 값 XYZ를 저장하는 경우가 많습니다. 예를 들어, 밤인지 낮인지를 구분할 수 있어야 합니다.
조명기구나 발광 물체는 실제로 다루기 까다롭습니다. 대부분의 렌더러에 부담을 주고 애플리케이션에 과도하기 때문에, 흑체 필라멘트 주위에 투명한 유리 전구를 모델링하는 경우는 거의 없습니다. 표면에서 나오는 균일한 조명이나 방향성 패턴으로 충분히 해결할 수 있습니다.
건축 모델을 위해 실제 조명기구를 정확히 구현해야 한다면, 조명 엔지니어링 분야의 표준을 참고해야 합니다. 이 경우 조명 엔지니어링과 컴퓨터 그래픽 양쪽에서 폭넓게 연구한 Greg Ward-Larsen과 Ian Ashdown의 작업을 살펴보시기 바랍니다. 그들의 연구를 읽으면 대부분의 문제를 해결할 수 있습니다.
7. Mathematical tools
물리 기반 렌더링에 필요한 수학적인 내용을 다뤄보겠습니다.
7.1 Monte Carlo and QMC
적분(integral)이 있다면, 적분 영역(domain) 내에서 랜덤한 지점들을 선택하고, 그 지점들에서 **피적분 함수(integrand)**를 평가한 다음, 그 평가값들을 평균하는 과정을 통해 답을 얻을 수 있습니다.
확률 밀도 함수()를 가진 하나의 무작위 샘플 에 대해 다음과 같은 결과가 나옵니다.
이 **보정 계수(correction factor)**를 생각하는 방식은, 를 밀집하게 샘플링하는 지점에서는 각 샘플을 더 적게 세어야 한다는 것입니다. 상수들은 모두 확률 밀도 함수(pdfs)의 정규화된(normalized) 특성에 포함되어 있습니다.
결과를 개선하려면, 더 큰 무작위 집합에 대해 단순히 평균을 내면 됩니다.
만약, 그리고 이것이 중요한 만약인데, 적분의 **차원(dimensionality)**이 낮다면(예: 1~6차원), 비(非)무작위 샘플을 사용하면 더 나은 답(더 적은 오차)을 얻을 수 있습니다. 한 가지 옵션은 지터링된(jittered) 또는 성층화된(stratified) 샘플입니다. 다른 하나는 준-규칙적(semi-regular) 또는 QMC(quasi-Monte Carlo, 준-몬테 카를로) 샘플입니다.
를 선택하는 것이 **시간 상수(time constant)**를 낮추는 반면, 좋은 샘플을 선택하는 것은 **시간 복잡도(time complexity)**를 낮춘다는 점에 유의하세요 (이것에 대한 2차원에서의 좋은 논의는 Mitchell [8]을 참조하세요).
문제는 **차원의 저주(curse of dimensionality)**인데, 이는 (구름 속에서의 10번의 반사와 같이) 고차원 적분에서는 "좋은" 샘플이 도움이 되지 않는다는 것을 의미합니다.
7.2 Density estimation and Metropoli
밀도 추정은 렌더링에서 흔히 사용되며, 포톤 매핑(photon mapping) [6]이 대표적인 예입니다. 여기서 일련의 점들은 올바른 에너지 값을 가지며(예: 나중에 참조할 수 있도록 표면의 에너지를 모델에 저장하여 '굽는(baking)' 경우), 밀도 추정은 이 점들을 생성한 기저 밀도(underlying density)를 추정합니다.
최근의 포톤 빔(photon beams)에 대한 연구는 이 접근법에 힘을 실어주었으며, 경로(paths)에 수학을 적용하는 것이 유용하다는 점을 강조합니다. 여기서 핵심은 라는 함수를 가지고 있다는 것인데, 여기서 는 확률 밀도 함수(pdf)입니다(적분 값이 1인 비음수 함수). 우리는 에 따라 분포된 일련의 샘플들을 가지고 있습니다. 따라서 이 샘플들을 흐릿하게(blur) 만들어 에 대한 합리적인 근사치를 얻으려고 합니다.
Animating the Metropolis algorithm
메트로폴리스(Metropolis)는 점들을 취하여 변이(mutate)시켜 그 밀도가 어떤 함수 에 비례하도록 만드는 방법입니다. 렌더링 방정식의 경우, 이 점들은 경로(paths)입니다. 혼란스러운 점은 경로에 대한 측도(measure)를 정의해야 한다는 것입니다. 경로는 길이가 다릅니다. 따라서 경로 공간에서의 "점"은 경로를 따라 있는 일련의 3차원 지점들로 정의되며, 이는 3개의 세그먼트(segment) 경로일 수도 있고 17개의 세그먼트 경로일 수도 있습니다. 고통을 감수하고(Bite the bullet) 경로 기반의 응용 측도 이론(applied measure theory)을 읽어보십시오(이것을 배우는 데 '하프-측도(half-measures)'는 없습니다).
더 일반적인 의미에서, 메트로폴리스는 임의의 점 집합과 인 임의의 함수를 취하며, 가 알려져 있지 않더라도 변이(mutations)를 사용하여 점 집합을 밀도 를 가진 점 집합으로 '진화(evolve)'시킵니다. 상수 는 다른 수단으로 추정되어야 합니다.
7.3 Functions on the sphere
많은 함수들은 구(sphere) 또는 반구(hemisphere) 상에 표현됩니다. BRDF, 산란(scattering)을 위한 위상 함수(phase functions), 표면에서의 입사광 또는 복사광, 체적 내에서의 조명, 그리고 먼 거리의 환경 조명 등이 있습니다. 문헌에서 일반적으로 사용되는 여러 기하학적 표현 방식이 있으며, 이들은 서로 다른 장단점을 가지고 있습니다. 구면의 다양한 매개변수화(parameterizations)에 대한 샘플링 효율성을 분석한 훌륭한 기술 보고서 [13]는 볼 가치가 있습니다.
구면 고조파(Spherical Harmonics, SH)는 문헌에서 푸리에 기저 함수(Fourier basis functions)의 구면 아날로그로 통용되지만, 컴퓨터 그래픽스에서는 실수형(real form)의 기저 함수가 사용됩니다 [12]. 구면 고조파는 직교 기저(orthogonal basis)를 형성하며, 이는 이 기저에서 표현된 두 함수 간의 적분을 계산하고 생성하는 효율적인 방법으로 이어집니다. 구면 고조파는 부드러운 신호를 저장하는 데 효율적이지만, 링잉 아티팩트(ringing artifacts)로 고통받을 수 있으며 높은 주파수의 신호를 표현하기 위해서는 많은 수의 계수(coefficients)가 필요합니다. 가장 중요한 특성은 기저가 회전에 대해 닫혀 있다(closed under rotation)는 것이며, 이는 기저 계수를 사용하여 신호를 회전시키는 효율적인 방법이 있다는 것입니다. 구면 고조파의 부분 집합인 영역 고조파(Zonal Harmonics)는 원형 대칭(circular symmetry)을 가진 함수를 나타내며, Z축 주위로 회전 변환 공식이 훨씬 더 효율적입니다. 이들은 종종 산란의 위상 함수에 사용됩니다.
웨이블릿(Wavelets)은 종종 큐브 맵(cube maps)에서 잘 작동하며 여러 주파수에서 신호를 포착하는 데 탁월합니다. 구면 고조파가 어려움을 겪는 높은 주파수도 포함됩니다. 투영(projection), 평가 및 희소 행렬(sparse results) 생성에 대한 효율적인 공식이 있지만, 몇 가지 단점이 있습니다. 면(face)의 중심에서의 미분 입체각(differential solid angle)이 모서리보다 5배 이상 크다는 것입니다. 이는 회전 시 주파수가 누출될 수 있다는 것을 의미하며, 최악의 경우를 방지하기 위해 신중하게 사전 필터링해야 합니다. 또한 신호를 주어진 정확도 수준에서 표현하는 데 필요한 0이 아닌 계수의 수에 큰 변화를 야기할 수 있으며, 임계값 처리(thresholding) 시 깜빡임(flickering)이 발생할 수 있습니다. 그럼에도 일반적인 고주파 신호를 표현하고 싶다면 최선의 선택입니다.
구면 방사 기저 함수(Spherical Radial Basis Functions, SRBFs)는 대부분 가우시안(Gaussians) 형태이며, 회전시키기가 쉽고, 적분을 계산하는 효율적인 공식을 가지고 있으며 다양한 주파수를 나타낼 수 있습니다. 한 가지 단점은 웨이블릿이나 구면 고조파와 달리 비선형 투영(non-linear projection)을 수반하기 때문에 신호를 투영하는 것이 훨씬 더 어렵다는 것입니다 [14].
8. 렌더러 작성하기
렌더링 알고리즘에는 몇 가지 주요 종류가 있습니다.
주요 렌더링 알고리즘 종류
•
경로 추적(path tracing): 카메라에서 몬테 카를로 광선을 보냅니다.
•
포톤 추적(photon tracing): 광원에서 몬테 카를로 광선을 보냅니다.
•
양방향 경로 추적(bidirectional path tracing): 각 방향에서 부분 경로를 생성하여 서로 연결함으로써 광범위한 빛-눈 경로를 얻습니다.
•
메트로폴리스(Metropolis): 초기 경로 세트에서 시작하여 메트로폴리스 알고리즘으로 변이시킵니다. 양방향 경로 추적이 일반적으로 사용됩니다.
•
라디오시티(Radiosity): 유한 요소 해법을 수행하고 그 결과를 화면에 투영합니다.
다양한 변형이 존재합니다. 예를 들어, 포톤 트레이서는 얼룩덜룩해 보일 수 있지만, QMC(Quasi-Monte Carlo)를 사용하면 더 부드러운 결과를 얻을 수 있습니다. 한 번의 바운스 경로 추적은 부드러운 표면으로 제한될 수 있습니다. 포톤 또는 경로 추적으로 확산 반사체를 처리할 수 있으며, 조명을 텍스처에 굽거나 구면 고조파의 적은 수의 계수로 저장할 수 있습니다. "역방향(backward)" 및 "순방향(forward)"이라는 용어는 종종 혼란을 야기하므로 대부분의 사람들이 오늘날 이를 피합니다.
8.1 디버깅
물리 기반 메서드를 디버깅하는 것은 어렵습니다. 잘못된 그림도 그럴듯하게 보이는 경우가 많기 때문입니다. 첫 번째 디버깅 방법은 "용광로(the furnace)"를 사용하는 것입니다. 모든 표면이 알베도 을 가진 확산 반사체이고, 모든 표면이 휘도 를 방출하는 발광체라고 가정합니다. 기하학적 구성에 관계없이 최종 휘도()는 다음과 같습니다.
또 다른 좋은 디버깅 도구는 온라인에서 데이터와 사진을 제공하는 코넬 대학교의 "코넬 박스(Cornell Box)"입니다.
마지막으로, 렌더링 결과물을 온라인 이미지들과 비교하며 확인해 보십시오.
References
November 2012
Conference: SIGGRAPH Asia 2012 Courses








.png&blockId=29c0b1ff-a61e-8016-b51c-fc7cdf5cb56f)
.png&blockId=29c0b1ff-a61e-807a-8838-d17fe3a8d656)