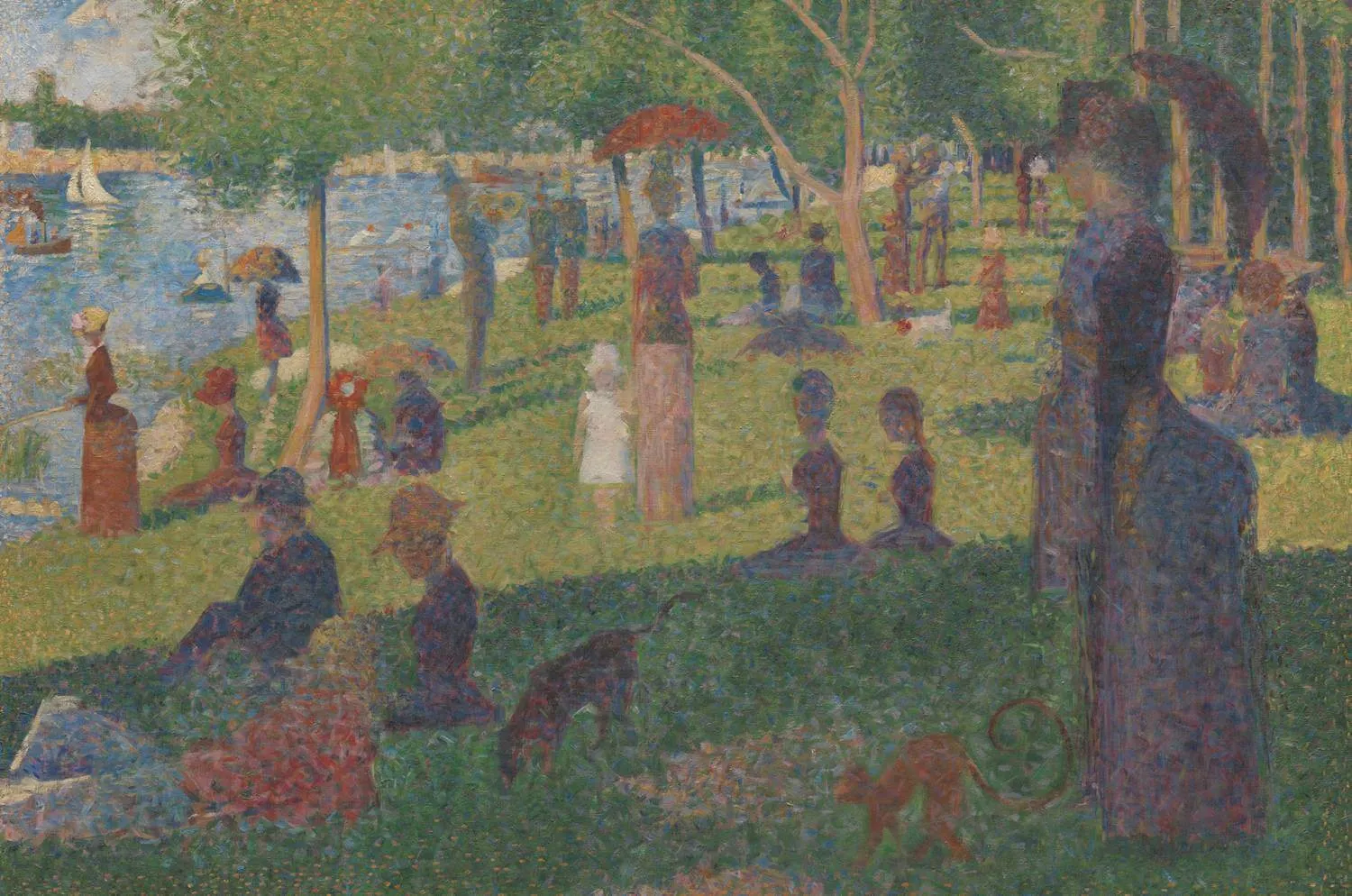Normal Mapping - Dx12, HLSL
우리의 모든 장면(scene)은 메시(mesh)들로 가득 차 있고, 각 메시들은 수백 개, 어쩌면 수천 개의 삼각형으로 이루어져 있다. 우리는 이 평평한 삼각형들에 2D 텍스처를 감싸 입혀서, 폴리곤이 그저 작은 평평한 삼각형들에 불과하다는 사실을 숨기며 사실감을 높였다. 텍스처는 도움이 되지만, 메시를 가까이에서 자세히 보면 여전히 밑바탕의 평평한 표면이 쉽게 보인다. 그러나 대부분의 실제 표면은 평평하지 않고 많은(울퉁불퉁한) 디테일을 보인다.
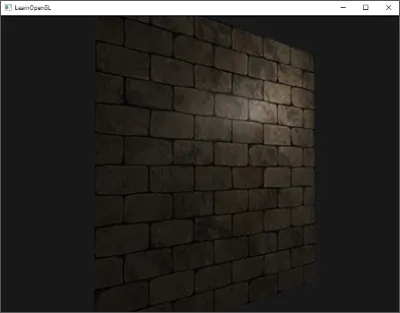
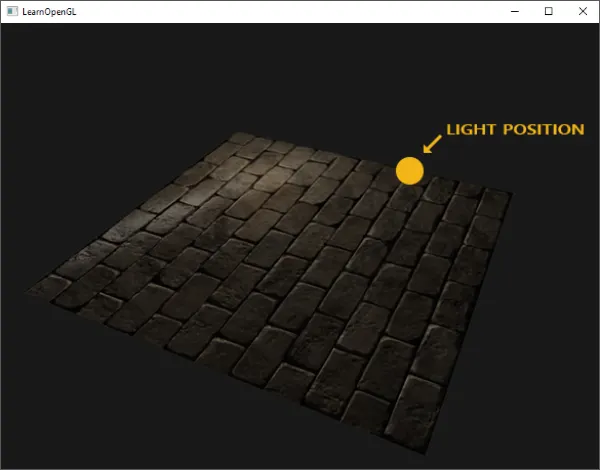
예를 들어, 벽돌 표면을 생각해보자. 벽돌 표면은 꽤 거친 표면이고 분명 완전히 평평하지 않다: 움푹 들어간 시멘트 줄이 있고, 아주 작은 구멍과 균열 같은 세밀한 디테일이 많다. 이런 벽돌 표면을 조명이 있는 장면에서 본다면 몰입감은 쉽게 깨진다. 아래에서는 점광원으로 조명된 평면에 벽돌 텍스처가 적용된 모습을 볼 수 있다.
점광원으로 조명된 벽돌 표면. 그다지 현실적이지 않다; 평평한 구조가 이제 매우 분명하다.
조명은 작은 균열과 구멍을 전혀 고려하지 않고 벽돌 사이의 깊은 줄을 완전히 무시한다; 표면은 완전히 평평해 보인다. 깊이나 다른 디테일 때문에 일부 표면이 덜 조명된 것처럼 가장하기 위해 스페큘러 맵을 사용함으로써 평평해 보이는 느낌을 부분적으로 고칠 수 있지만, 이는 진짜 해결책이라기보다 요령에 가깝다. 우리가 필요한 것은 표면의 모든 작은 깊이 같은 디테일을 조명 시스템에 알려줄 수 있는 어떤 방법이다.
이것을 빛의 관점에서 생각해보면: 왜 표면이 완전히 평평한 표면처럼 조명되는가? 답은 표면의 법선 벡터(normal vector)다. 조명 기법의 관점에서, 객체의 형태를 결정하는 유일한 방법은 그 표면에 수직인 법선 벡터뿐이다. 벽돌 표면은 단 하나의 법선 벡터만 가지며, 그 결과 표면은 이 법선 벡터의 방향에 따라 균일하게 조명된다. 그렇다면, 조각(fragment)마다 모두 동일한 표면 법선 대신, 각 조각마다 서로 다른 픽셀 단위(per-fragment) 법선을 사용하면 어떨까? 이렇게 하면 표면의 작은 디테일에 따라 법선 벡터를 약간씩 빗나가게 할 수 있고; 이것은 표면이 훨씬 더 복잡하다는 환상을 준다:
표면 단위 법선과 픽셀 단위 법선을 보여주는 표면
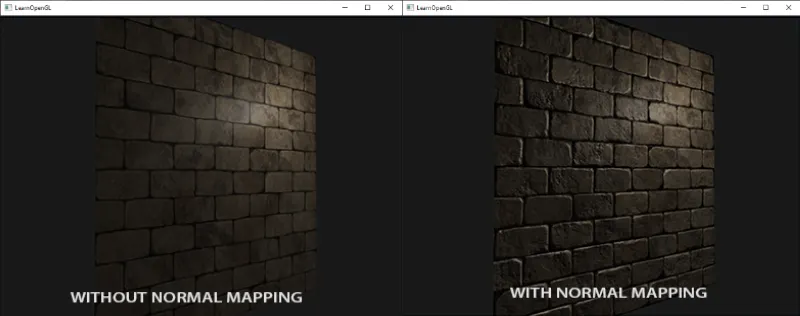
픽셀 단위 법선을 사용함으로써 우리는 조명을 속여 표면이(법선 벡터에 수직인) 아주 작은 평면들로 이루어진 것처럼 믿게 만들어, 표면의 디테일을 엄청나게 끌어올릴 수 있다. 표면 단위 법선 대신 픽셀 단위 법선을 사용하는 이 기술을 노멀 매핑(normal mapping) 또는 범프 매핑(bump mapping) 이라고 부른다. 이것을 벽돌 평면에 적용하면 대략 다음과 같이 보인다:
노멀 매핑 전/후의 표면
보는 바와 같이, 상대적으로 낮은 비용으로 엄청난 디테일 향상을 제공한다. 우리는 각 조각마다 법선 벡터만 바꾸기 때문에 조명 방정식을 바꿀 필요는 없다. 이제 보간된 표면 법선 대신 픽셀 단위 법선을 조명 알고리즘에 전달한다. 나머지는 조명이 처리한다.
Normal mapping
노멀 매핑이 작동하도록 하려면 픽셀 단위 법선이 필요하다. 디퓨즈와 스페큘러 맵에서 했던 것과 유사하게, 2D 텍스처를 사용해 픽셀 단위 법선 데이터를 저장할 수 있다. 이렇게 하면 특정 조각에 대한 법선 벡터를 얻기 위해 2D 텍스처를 샘플링할 수 있다.
법선 벡터는 기하학적 개체이고 텍스처는 일반적으로 색상 정보에만 사용되므로, 텍스처에 법선 벡터를 저장한다는 것이 바로 명확하지 않을 수 있다. 텍스처의 색상 벡터를 생각해보면 r, g, b 성분을 가진 3차원 벡터로 표현된다. 이와 유사하게 법선 벡터의 x, y, z 성분을 해당하는 색상 성분에 저장할 수 있다. 법선 벡터는 -1과 1 사이의 범위를 가지므로 먼저 [0,1]로 매핑된다:
vec3 rgb_normal = normal * 0.5 + 0.5; // [-1,1]을 [0,1]로 변환
GLSL
복사
이와 같이 법선 벡터를 RGB 색상 성분으로 변환하면, 표면의 형상에서 파생된 픽셀 단위 법선을 2D 텍스처에 저장할 수 있다. 이 장의 시작 부분에 나온 벽돌 표면의 예시 노멀 맵은 아래와 같다:
노멀 매핑에서의 노멀 맵 이미지
이 (그리고 온라인에서 흔히 구할 수 있는 대부분의 노멀 맵)는 푸르스름한 색조를 띤다.
이는 대부분의 픽셀 법선이 양의 Z축 방향 (0, 0, 1) 을 향해 있기 때문이다 — 즉, 노멀 벡터의 Z 성분이 높아 파란색 계열로 보인다.
색상의 편차는 각 픽셀의 노멀이 얼마나 표면 기준 축에서 벗어나 있는지를 나타낸다.
예를 들어, 벽돌 표면의 윗부분은 양의 Y축 방향 (0, 1, 0) 쪽으로 더 기울어져 있으므로 녹색이 강하게 나타난다.
반대로 움푹 파인 부분은 Z 성분이 약해지면서 자주색·보라색 계열로 표현된다.
이러한 색 변화는 실제로 표면이 입체적으로 보이도록 깊이감을 만들어낸다.
DirectX에서는 텍스처 좌표 체계가 OpenGL과 반대 방향이다.
OpenGL은 텍스처 원점을 좌하단(0,0) 으로 두지만, DirectX는 좌상단(0,0) 이다.
따라서 OpenGL 기준으로 제작된 노멀 맵을 DirectX에서 그대로 사용할 경우,
V축(또는 green 채널) 의 방향이 뒤집혀 조명이 반대로 들어가는 현상이 발생한다.
이 문제를 해결하려면 다음 중 한 가지를 적용해야 한다:
1.
셰이더에서 G 채널 반전:
픽셀 셰이더(HLSL)에서 노멀 맵 샘플링 후,
normal.g = 1.0f - normal.g; 또는 normal.y = -normal.y; 로 반전시킨다.
2.
텍스처 로드 시 V 좌표 반전:
모델 로더나 머티리얼 시스템에서 텍스처 좌표의 V 성분을 uv.y = 1 - uv.y; 로 변환한다.
// ==== RootSignature / Registers ====
// Texture2D gNormalMap : register(t1);
// SamplerState gSamplerLinear : register(s0);
// === 옵션 스위치 ===
// GL 제작 텍스처를 DX에서 사용할 때 흔한 두 가지 이슈를 토글:
#define FLIP_UV_V 0 // 1이면 uv.y = 1 - uv.y
#define FLIP_NORMALMAP_G 0 // 1이면 normal.g = -normal.g
// --------------------------------------------------------------
// 권장형: T/B/N을 개별 float3로 전달 (인터폴레이션 제어/디버깅 용이)
// --------------------------------------------------------------
struct PSIn_TBNVectors
{
float2 UV : TEXCOORD0;
float3 T : TEXCOORD1; // world-space tangent
float3 B : TEXCOORD2; // world-space bitangent
float3 N : TEXCOORD3; // world-space normal
};
float4 PS_NormalSample_Vectors(PSIn_TBNVectors pin) : SV_TARGET
{
float2 uv = pin.UV;
#if FLIP_UV_V
uv.y = 1.0f - uv.y;
#endif
// 노멀맵 샘플 → [0,1] → [-1,1]
float3 nTS = gNormalMap.Sample(gSamplerLinear, uv).rgb;
#if FLIP_NORMALMAP_G
nTS.g = 1.0f - nTS.g; // (= -nTS.g if already in [-1,1] below)
#endif
nTS = nTS * 2.0f - 1.0f;
// TS → WS : row-vector * matrix
float3x3 TBN = float3x3(normalize(pin.T), normalize(pin.B), normalize(pin.N));
float3 Nws = normalize(mul(nTS, TBN));
// ... (조명 계산)
return float4(Nws * 0.5f + 0.5f, 1.0f); // 뷰용 출력(원하면 교체)
}
// --------------------------------------------------------------
// 대안형: TBN 행렬을 한 번에 전달
// --------------------------------------------------------------
struct PSIn_TBNMatrix
{
float2 UV : TEXCOORD0;
float3x3 TBN : TEXCOORD1; // world-space TBN (열벡터: T,B,N)
};
float4 PS_NormalSample_Matrix(PSIn_TBNMatrix pin) : SV_TARGET
{
float2 uv = pin.UV;
#if FLIP_UV_V
uv.y = 1.0f - uv.y;
#endif
float3 nTS = gNormalMap.Sample(gSamplerLinear, uv).rgb;
#if FLIP_NORMALMAP_G
nTS.g = 1.0f - nTS.g;
#endif
nTS = nTS * 2.0f - 1.0f;
float3 Nws = normalize(mul(nTS, pin.TBN));
// ... (조명 계산)
return float4(Nws * 0.5f + 0.5f, 1.0f);
}
GLSL
복사
여기서는 샘플링한 노멀 색을 [0,1]에서 [-1,1]로 재매핑하여, RGB 색상으로 매핑하는 과정을 역으로 수행한 뒤 다가올 조명 계산을 위해 샘플된 법선 벡터를 사용한다. 이 경우 우리는 Blinn-Phong 셰이더를 사용했다.
(주의: PBR 파이프라인이라면 금속성/거칠기(F0/roughness/metallic)를 사용한 BRDF로 대체.)
시간이 지나면서 광원(light source)을 천천히 움직이면 노멀 맵을 사용해 진정한 깊이감을 느낄 수 있다. 이 노멀 매핑 예제를 실행하면 이 장의 시작 부분에 표시된 것과 정확히 동일한 결과를 제공한다:
노멀 매핑 전/후의 표면
하지만 이 노멀 맵 사용을 크게 제한하는 한 가지 문제가 있다. 우리가 사용한 노멀 맵은 모든 법선 벡터가 어느 정도 양의 z 방향을 가리키고 있었다. 이것이 작동한 이유는 평면의 표면 법선 또한 양의 z 방향을 가리키고 있었기 때문이다. 그러나 동일한 노멀 맵을, 표면 법선 벡터가 양의 y 방향을 가리키는 바닥에 놓인 평면에 사용한다면 어떻게 될까?
탄젠트 공간 변환 없이 노멀 매핑된 평면 이미지 — 어색해 보임
조명이 올바르게 보이지 않는다! 이는 이 평면의 샘플된 법선들이 여전히 대체로 양의 z 방향을 가리키고 있기 때문인데, 사실 대부분 양의 y 방향을 가리켜야 한다. 그 결과 조명은 평면이 양의 z 방향을 향하고 있었을 때와 동일한 표면 법선을 가진다고 생각하게 되어; 조명이 잘못된다. 아래 이미지는 이 표면에서 샘플된 법선들이 대략 어떻게 보이는지를 보여준다:
탄젠트 공간 변환 없이 노멀을 표시한 평면 이미지 — 어색해 보임
보면 모든 법선이 다소 양의 z 방향을 가리키는데, 사실은 양의 y 방향을 가리켜야 한다. 이 문제의 한 가지 해결책은 표면의 가능한 각 방향마다 노멀 맵을 정의하는 것이다; 큐브의 경우 6개의 노멀 맵이 필요할 것이다. 그러나 수백 가지 이상의 가능한 표면 방향을 가질 수 있는 고급 메시들의 경우 이는 실행 불가능한 접근이다.
다른 해결책은 모든 조명을 다른 좌표 공간에서 수행하는 것이다: 노멀 맵 벡터가 항상 양의 z 방향을 가리키는 좌표 공간; 다른 모든 조명 벡터는 이 양의 z 방향을 기준으로 변환된다. 이렇게 하면 방향에 상관없이 항상 동일한 노멀 맵을 사용할 수 있다. 이 좌표 공간을 탄젠트 공간(tangent space) 이라고 한다.
Tangent space
노멀 맵의 법선 벡터는 탄젠트 공간으로 표현되며, 여기서 법선들은 항상 대략 양의 z 방향을 가리킨다. 탄젠트 공간은 삼각형 표면에 국소적인 공간이다: 법선들은 개별 삼각형의 로컬 기준 프레임에 상대적이다. 이것을 노멀 맵 벡터들의 로컬 공간이라고 생각하라; 최종 변환된 방향과 관계없이 모두 양의 z 방향을 가리키도록 정의된다. 특정 행렬을 사용하여 그다음 법선 벡터를 이 로컬 탄젠트 공간에서 월드 또는 뷰 좌표로 변환하여, 최종 매핑된 표면의 방향에 맞춰 정렬할 수 있다.
앞 절의 잘못된 노멀 매핑 표면이 양의 y 방향을 보고 있다고 하자. 노멀 맵은 탄젠트 공간에서 정의되므로, 문제를 해결하는 한 가지 방법은 법선을 탄젠트 공간에서 다른 공간으로 변환하는 행렬을 계산하여 표면의 법선 방향에 맞춰 정렬하는 것이다: 그러면 법선 벡터들은 모두 대략 양의 y 방향을 가리키게 된다. 탄젠트 공간의 훌륭한 점은 어떤 유형의 표면에 대해서도 이 행렬을 계산해 탄젠트 공간의 z 방향을 표면의 법선 방향에 제대로 맞출 수 있다는 것이다.
이러한 행렬을 TBN 행렬이라고 하며, 문자들은 Tangent(탄젠트), Bitangent(비탄젠트), Normal(법선) 벡터를 나타낸다. 이 행렬을 구성하려면 이 벡터들이 필요하다. 탄젠트 공간 벡터를 다른 좌표 공간으로 변환하는 기저 변경(change-of-basis) 행렬을 구성하기 위해서는, 노멀 맵의 표면에 정렬된 서로 수직인 세 벡터, 즉 위(up), 오른쪽(right), 앞(forward) 벡터가 필요하다; 이는 카메라 장에서 했던 것과 유사하다.
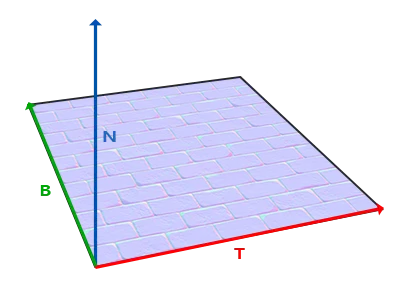
우리는 이미 위 벡터를 알고 있는데, 그것은 표면의 법선 벡터다. 오른쪽과 앞 벡터는 각각 탄젠트와 비탄젠트 벡터다. 다음의 표면 이미지에는 표면 위의 이 세 벡터가 모두 표시되어 있다:
표면 위의 탄젠트, 비탄젠트, 법선 벡터
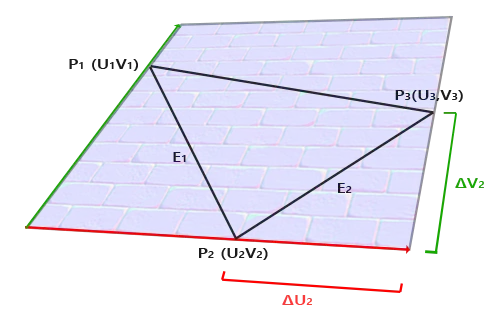
탄젠트와 비탄젠트 벡터를 계산하는 것은 법선 벡터만큼 간단하지 않다. 이미지에서 볼 수 있듯이 노멀 맵의 탄젠트와 비탄젠트 벡터의 방향은 우리가 표면의 텍스처 좌표를 정의하는 방향과 정렬되어 있다. 우리는 이 사실을 사용해 각 표면의 탄젠트와 비탄젠트 벡터를 계산할 것이다. 이를 얻으려면 약간의 수학이 필요하다; 다음 이미지를 보라:
TBN 행렬 계산에 필요한 DirectX 12 표면의 에지
이미지에서 볼 수 있듯이 삼각형의 한 에지 E2의 텍스처 좌표 차(ΔU2와 ΔV2)는 탄젠트 벡터 T와 비탄젠트 벡터 B의 방향과 동일한 방향으로 표현된다. 이 때문에 삼각형의 표시된 두 에지 E1과 E2를 탄젠트 벡터 T와 비탄젠트 벡터 B의 선형 결합으로 쓸 수 있다:
다음과 같이도 쓸 수 있다:
E는 두 삼각형 위치의 차 벡터로 계산할 수 있고, ΔU와 ΔV는 그들의 텍스처 좌표 차이다. 그러면 우리는 두 개의 미지수(탄젠트 T와 비탄젠트 B)와 두 개의 방정식이 남는다. 대수학 수업에서 기억하듯이 이것으로 T와 B를 풀 수 있다.
마지막 방정식은 다른 형태로 쓸 수 있다: 행렬 곱의 형태로:
머릿속으로 행렬 곱을 시각화하여 이게 실제로 같은 방정식임을 확인하라. 방정식을 행렬 형태로 다시 쓰는 장점은 T와 B를 푸는 것이 더 이해하기 쉬워진다는 것이다. 만약 ΔUΔV 행렬의 역행렬을 방정식의 양변에 곱하면 다음과 같이 된다:
이로써 T와 B를 풀 수 있다. 이것은 델타 텍스처 좌표 행렬의 역을 계산해야 함을 의미한다. 행렬의 역 계산의 수학적 세부사항에는 들어가지 않겠지만, 대략적으로 행렬식(determinant)의 1/값에 그 수반행렬(adjugate matrix)을 곱하는 것으로 번역된다:
이 최종 방정식은 삼각형의 두 에지와 텍스처 좌표로부터 탄젠트 벡터 T와 비탄젠트 벡터 B를 계산하는 공식을 제공한다.
이 수학을 완전히 이해하지 못하더라도 걱정하지 말라. 삼각형의 정점과 그 텍스처 좌표(텍스처 좌표는 탄젠트 벡터와 동일한 공간에 있기 때문에)로부터 탄젠트와 비탄젠트를 계산할 수 있다는 사실만 이해한다면 절반은 온 것이다.
Manual calculation of tangents and bitangents
이전 데모에서는 양의 z 방향을 바라보는 단순한 노멀 매핑 평면이 있었다. 이번에는 탄젠트 공간을 사용하여 노멀 매핑을 구현해, 이 평면을 원하는 대로 방향을 바꿔도 노멀 매핑이 여전히 동작하도록 하고자 한다. 앞서 논의한 수학을 사용하여 이 표면의 탄젠트와 비탄젠트 벡터를 수동으로 계산할 것이다.
평면이 다음 벡터들로 구성되어 있다고 가정하자(두 삼각형은 1,2,3과 1,3,4):
// positions
Vector3 pos1(-1.0, 1.0, 0.0);
Vector3 pos2(-1.0, -1.0, 0.0);
Vector3 pos3( 1.0, -1.0, 0.0);
Vector3 pos4( 1.0, 1.0, 0.0);
// texture coordinates
Vector2 uv1(0.0, 1.0);
Vector2 uv2(0.0, 0.0);
Vector2 uv3(1.0, 0.0);
Vector2 uv4(1.0, 1.0);
// normal vector
Vector3 nm(0.0, 0.0, 1.0);
C++
복사
먼저 첫 번째 삼각형의 에지와 델타 UV 좌표를 계산한다:
Vector3 edge1 = pos2 - pos1;
Vector3 edge2 = pos3 - pos1;
Vector2 deltaUV1 = uv2 - uv1;
Vector2 deltaUV2 = uv3 - uv1;
C++
복사
탄젠트와 비탄젠트를 계산하는 데 필요한 데이터로 이전 절의 방정식을 따르기 시작한다:
float f = 1.0f / (deltaUV1.x * deltaUV2.y - deltaUV2.x * deltaUV1.y);
tangent1.x = f * (deltaUV2.y * edge1.x - deltaUV1.y * edge2.x);
tangent1.y = f * (deltaUV2.y * edge1.y - deltaUV1.y * edge2.y);
tangent1.z = f * (deltaUV2.y * edge1.z - deltaUV1.y * edge2.z);
bitangent1.x = f * (-deltaUV2.x * edge1.x + deltaUV1.x * edge2.x);
bitangent1.y = f * (-deltaUV2.x * edge1.y + deltaUV1.y * edge2.y);
bitangent1.z = f * (-deltaUV2.x * edge1.z + deltaUV1.x * edge2.z);
[...] // 평면의 두 번째 삼각형에 대해서도 유사한 절차
C++
복사
여기서 우리는 먼저 f로 방정식의 분수 부분을 미리 계산한 다음, 각 벡터 성분에 대해 해당 행렬 곱을 f로 곱한다. 이 코드를 최종 방정식과 비교하면 이것이 직접적인 번역임을 알 수 있다. 삼각형은 항상 평평한 형태이므로, 각 삼각형의 정점 모두에 대해 동일하므로 삼각형당 하나의 탄젠트/비탄젠트 쌍만 계산하면 된다.
결과 탄젠트와 비탄젠트 벡터는 각각 (1,0,0)과 (0,1,0)의 값을 가져야 하며, 여기에 법선 (0,0,1)과 함께 직교하는 TBN 행렬을 형성한다. 평면에 시각화하면 TBN 벡터는 다음과 같이 보일 것이다:
평면 위에 시각화된 TBN 벡터 이미지
정점마다 탄젠트와 비탄젠트 벡터를 정의했으므로 이제 올바른 노멀 매핑 구현을 시작할 수 있다.
Tangent space normal mapping
노멀 매핑이 동작하도록 하려면, 먼저 셰이더에서 TBN 행렬을 생성해야 한다. 그러기 위해 앞서 계산한 탄젠트와 비탄젠트 벡터를 정점 속성으로 정점 셰이더에 전달한다:
struct VSInput
{
float3 Position : POSITION;
float3 Normal : NORMAL;
float2 TexCoord : TEXCOORD0;
float4 Tangent : TANGENT; // xyz=tangent, w=handedness(+1/-1)
// Bitangent는 셰이더에서 cross로 복원
};
struct VSOut_TBNtoWS
{
float4 PosH : SV_POSITION;
float3 PosWS : TEXCOORD0;
float2 UV : TEXCOORD1;
float3x3 TBN : TEXCOORD2; // world-space TBN
// 실전 권장: T,B,N을 각각 TEXCOORD2/3/4로 float3 전달
};
struct VSOut_WStoTBN
{
float4 PosH : SV_POSITION;
float2 UV : TEXCOORD0;
float3 TangentLight : TEXCOORD1;
float3 TangentView : TEXCOORD2;
float3 TangentPos : TEXCOORD3;
};
GLSL
복사
그런 다음 정점 셰이더의 main 함수 내에서 TBN 행렬을 생성한다:
// cbuffer 정렬 주의: float3 뒤에는 16바이트 정렬을 위해 패딩 필요
cbuffer ObjectCB : register(b0)
{
float4x4 gWorld;
float4x4 gViewProj;
float3 gLightPosWS; float _pad0;
float3 gCameraPosWS; float _pad1;
}
VSOut_TBNtoWS VS_TBNtoWS(VSInput vin)
{
VSOut_TBNtoWS v;
float4 posWS4 = mul(float4(vin.Position, 1.0f), gWorld);
float3 posWS = posWS4.xyz;
// 비균일 스케일이 있다면 gWorld의 inverse-transpose(3x3) 사용 권장
float3 N = normalize(mul(float4(vin.Normal, 0.0f), gWorld).xyz);
float3 T = normalize(mul(float4(vin.Tangent.xyz, 0.0f), gWorld).xyz);
// Gram-Schmidt 재직교화
T = normalize(T - dot(T, N) * N);
float3 B = normalize(cross(N, T)) * vin.Tangent.w;
v.TBN = float3x3(T, B, N);
v.PosWS = posWS;
v.UV = vin.TexCoord;
v.PosH = mul(posWS4, gViewProj);
return v;
}
GLSL
복사
여기서는 먼저 모든 TBN 벡터를 우리가 작업하려는 좌표계로 변환하는데, 이 경우 모델 행렬을 곱하므로 월드 공간이다. 그런 다음 관련 열 벡터들을 직접 mat3 생성자에 공급하여 실제 TBN 행렬을 만든다. 정말 정밀하게 하려면 벡터들의 방향에만 관심이 있으므로 TBN 벡터들을 노멀 매트릭스(월드의 inverse-transpose 3×3) 로 곱했을 것이다.
기술적으로 정점 셰이더에 비탄젠트 변수가 꼭 필요하지는 않다. 세 TBN 벡터는 서로 수직이므로, 정점 셰이더에서 T와 N의 외적을 취해 비탄젠트를 직접 계산할 수 있다:
float3 B = cross(N, T) * vin.Tangent.w;
이제 TBN 행렬을 얻었으니, 어떻게 사용할까? 노멀 매핑을 위해 TBN 행렬을 사용하는 방법은 두 가지가 있으며, 둘 다 보여줄 것이다:
1.
탄젠트에서 월드 공간으로 임의의 벡터를 변환하는 TBN 행렬을 픽셀 셰이더(PS) 에 전달하고, 이 TBN 행렬을 사용해 샘플된 노멀을 탄젠트 공간에서 월드 공간으로 변환한다; 그러면 노멀은 다른 조명 변수들과 같은 공간에 있게 된다.
2.
월드 공간에서 탄젠트 공간으로 임의의 벡터를 변환하는 TBN 행렬의 역행렬을 취하고, 노멀이 아니라 다른 관련 조명 변수들을 탄젠트 공간으로 변환하는 데 이 행렬을 사용한다; 그러면 노멀은 다시 다른 조명 변수들과 같은 공간에 있게 된다.
첫 번째 경우를 살펴보자. 노멀 맵에서 샘플한 법선 벡터는 탄젠트 공간으로 표현되는 반면, 다른 조명 벡터들(빛과 시선 방향)은 월드 공간으로 표현된다. TBN 행렬을 픽셀 셰이더에 전달함으로써, 샘플된 탄젠트 공간 노멀에 이 TBN 행렬을 곱해 법선 벡터를 다른 조명 벡터들과 같은 기준 공간으로 변환할 수 있다. 이렇게 하면 모든 조명 계산(특히 내적)이 타당해진다.
TBN 행렬을 픽셀 셰이더로 보내는 것은 간단하다:
VSOut_WStoTBN VS_WStoTBN(VSInput vin)
{
VSOut_WStoTBN v;
float4 posWS4 = mul(float4(vin.Position, 1.0f), gWorld);
float3 posWS = posWS4.xyz;
// 비균일 스케일 고려 시 inverse-transpose(3x3) 권장
float3 N = normalize(mul(float4(vin.Normal, 0.0f), gWorld).xyz);
float3 T = normalize(mul(float4(vin.Tangent.xyz, 0.0f), gWorld).xyz);
T = normalize(T - dot(T, N) * N);
float3 B = normalize(cross(N, T)) * vin.Tangent.w;
float3x3 TBN = float3x3(T, B, N);
float3x3 TBNinv = transpose(TBN); // 직교 가정 → inverse == transpose
v.TangentLight = mul(gLightPosWS - posWS, TBNinv);
v.TangentView = mul(gCameraPosWS - posWS, TBNinv);
v.TangentPos = mul(posWS, TBNinv);
v.UV = vin.TexCoord;
v.PosH = mul(posWS4, gViewProj);
return v;
}
GLSL
복사
픽셀 셰이더에서는 유사하게 float3x3를 입력 대신, 여기선 변환된 벡터들을 직접 사용한다:
// (설명 전개용 인터페이스; 실제 입력은 VSOut_* 구조와 일치)
struct VS_OUT {
float3 FragPos; // (사용하지 않는다면 제거 가능)
float2 TexCoords;
float3x3 TBN; // 방법 A를 쓸 때
};
GLSL
복사
이 TBN 행렬을 사용하여 이제 노멀 매핑 코드를 탄젠트→월드 공간 변환을 포함하도록 업데이트할 수 있다:
Texture2D gBaseColor : register(t0);
Texture2D gNormalMap : register(t1);
SamplerState gSamplerLinear : register(s0);
float4 PS_TBNtoWS(VSOut_TBNtoWS pin) : SV_TARGET
{
float3 albedo = gBaseColor.Sample(gSamplerLinear, pin.UV).rgb;
float3 nTS = gNormalMap.Sample(gSamplerLinear, pin.UV).rgb * 2.0f - 1.0f;
// 필요시 그린 채널 반전:
// nTS.g = -nTS.g;
float3 N = normalize(mul(nTS, pin.TBN)); // (row) * (3x3)
float3 L = normalize(gLightPosWS - pin.PosWS);
float3 V = normalize(gCameraPosWS - pin.PosWS);
float3 H = normalize(L + V);
float diff = saturate(dot(N, L));
float spec = pow(saturate(dot(N, H)), 64.0f);
float3 color = albedo * diff + spec.xxx;
return float4(color, 1.0f);
}
GLSL
복사
결과 노멀이 이제 월드 공간에 있으므로, 다른 픽셀 셰이더 코드를 변경할 필요가 없다. 조명 코드는 법선 벡터가 월드 공간에 있다고 가정하기 때문이다.
두 번째 경우도 살펴보자. 여기서는 TBN 행렬의 역을 취해 모든 관련 월드 공간 벡터를 샘플된 노멀 벡터가 있는 공간, 즉 탄젠트 공간으로 변환한다. TBN 행렬의 구성은 동일하지만, 픽셀 셰이더로 보내기 전에 먼저 행렬을 반전시킨다:
VSOut_WStoTBN VS_WStoTBN(VSInput vin)
{
VSOut_WStoTBN v;
float4 posWS4 = mul(float4(vin.Position, 1.0f), gWorld);
float3 posWS = posWS4.xyz;
float3 N = normalize(mul(float4(vin.Normal, 0.0f), gWorld).xyz);
float3 T = normalize(mul(float4(vin.Tangent.xyz, 0.0f), gWorld).xyz);
T = normalize(T - dot(T, N) * N);
float3 B = normalize(cross(N, T)) * vin.Tangent.w;
float3x3 TBN = float3x3(T, B, N);
float3x3 TBNinv = transpose(TBN); // 직교 가정 → inverse == transpose
v.TangentLight = mul(gLightPosWS - posWS, TBNinv);
v.TangentView = mul(gCameraPosWS - posWS, TBNinv);
v.TangentPos = mul(posWS, TBNinv);
v.UV = vin.TexCoord;
v.PosH = mul(posWS4, gViewProj);
return v;
}
GLSL
복사
여기서 역함수 대신 전치(transpose) 함수를 사용한다는 점에 주목하라. 직교 행렬(각 축이 서로 수직인 단위 벡터)들의 훌륭한 성질은, 직교 행렬의 전치가 그 역과 같다는 것이다. 이는 역이 비용이 큰 반면 전치는 그렇지 않기 때문에 훌륭한 성질이다.
픽셀 셰이더 내에서는 법선 벡터를 변환하지 않고, 오히려 다른 관련 벡터들, 즉 lightDir와 viewDir 벡터를 탄젠트 공간으로 변환한다. 그렇게 하면 각 벡터가 동일한 좌표 공간(탄젠트 공간)에 있게 된다.
float4 PS_WStoTBN(VSOut_WStoTBN pin) : SV_TARGET
{
float3 albedo = gBaseColor.Sample(gSamplerLinear, pin.UV).rgb;
float3 nTS = gNormalMap.Sample(gSamplerLinear, pin.UV).rgb * 2.0f - 1.0f;
// 필요시:
// nTS.g = -nTS.g;
float3 N = normalize(nTS);
float3 L = normalize(pin.TangentLight);
float3 V = normalize(pin.TangentView);
float3 H = normalize(L + V);
float diff = saturate(dot(N, L));
float spec = pow(saturate(dot(N, H)), 64.0f);
float3 color = albedo * diff + spec.xxx;
return float4(color, 1.0f);
}
GLSL
복사
두 번째 접근은 더 많은 작업처럼 보이고 픽셀 셰이더에서 행렬 곱도 필요하다. 그렇다면 왜 두 번째 접근을 신경 써야 할까?
월드에서 탄젠트 공간으로 벡터를 변환하는 것은, 픽셀 셰이더가 아니라 정점 셰이더에서 모든 관련 조명 벡터를 탄젠트 공간으로 변환할 수 있다는 추가 이점이 있다. 이는 lightPos와 viewPos가 픽셀마다 업데이트되지 않고, fs_in.FragPos에 대해서는 그 탄젠트 공간 위치를 정점 셰이더에서 계산한 다음 픽셀 보간이 일을 하도록 둘 수 있기 때문에 가능하다. 픽셀 셰이더에서 벡터를 탄젠트 공간으로 변환할 실질적인 필요는 없다. 반면 첫 번째 접근에서는 샘플된 노멀 벡터가 각 픽셀 셰이더 실행에 특화되어 있으므로 필요하다. (추가 메모: 이 때문에 방법 B가 성능상 일반적으로 유리하다.)
따라서 TBN 행렬의 역을 픽셀 셰이더로 보내는 대신, 탄젠트 공간의 광원 위치, 시점 위치, 정점 위치를 픽셀 셰이더로 보낸다. 이렇게 하면 픽셀 셰이더에서 행렬 곱을 수행할 필요가 없다. 정점 셰이더는 픽셀 셰이더보다 훨씬 덜 자주 실행되므로, 이는 좋은 최적화다. 이것이 또한 이 접근이 종종 선호되는 이유다.
out VS_OUT {
float3 FragPos;
float2 TexCoords;
float3 TangentLightPos;
float3 TangentViewPos;
float3 TangentFragPos;
} vs_out;
uniform float3 lightPos;
uniform float3 viewPos;
[...]
void main()
{
[...]
float3x3 TBN = transpose(float3x3(T, B, N));
vs_out.TangentLightPos = mul(lightPos - FragPosWS, TBN); // WS→TS
vs_out.TangentViewPos = mul(viewPos - FragPosWS, TBN);
vs_out.TangentFragPos = mul(FragPosWS, TBN);
}
GLSL
복사
픽셀 셰이더에서는 이 새로운 입력 변수들을 사용해 탄젠트 공간에서 조명 계산을 한다. 법선 벡터는 이미 탄젠트 공간에 있으므로, 조명은 타당하다.
탄젠트 공간에 노멀 매핑을 적용하면, 이 장의 시작 부분에서 가졌던 결과와 유사한 결과를 얻어야 한다. 이번에는 원하는 대로 평면을 어떤 방향으로든 배치할 수 있고 조명은 여전히 올바를 것이다:
// 시간/회전축
float t = GetTimeSeconds(); // 사용자 타이머
XMVECTOR axis = XMVector3Normalize(XMVectorSet(1.0f, 0.0f, 1.0f, 0.0f));
// 월드/뷰/프로젝션
XMMATRIX world = XMMatrixRotationAxis(axis, XMConvertToRadians(-10.0f) * t);
XMMATRIX view = /* 카메라 */;
XMMATRIX proj = /* 투영 */;
// CB 채우기 (C++ 측은 XMFLOAT 대신 Vector/배열 사용)
struct ObjectCB {
float gWorld[16];
float gViewProj[16];
Vector3 gLightPosWS; float _pad0;
Vector3 gCameraPosWS; float _pad1;
};
// 행렬 저장(전치 포함) 헬퍼
auto StoreMatrix = [](float out[16], const XMMATRIX& M){
XMMATRIX T = XMMatrixTranspose(M);
out[0] = T.r[0].m128_f32[0]; out[1] = T.r[0].m128_f32[1]; out[2] = T.r[0].m128_f32[2]; out[3] = T.r[0].m128_f32[3];
out[4] = T.r[1].m128_f32[0]; out[5] = T.r[1].m128_f32[1]; out[6] = T.r[1].m128_f32[2]; out[7] = T.r[1].m128_f32[3];
out[8] = T.r[2].m128_f32[0]; out[9] = T.r[2].m128_f32[1]; out[10]= T.r[2].m128_f32[2]; out[11]= T.r[2].m128_f32[3];
out[12]= T.r[3].m128_f32[0]; out[13]= T.r[3].m128_f32[1]; out[14]= T.r[3].m128_f32[2]; out[15]= T.r[3].m128_f32[3];
};
ObjectCB cb{};
StoreMatrix(cb.gWorld, world);
StoreMatrix(cb.gViewProj, view * proj);
cb.gLightPosWS = {Lx, Ly, Lz};
cb.gCameraPosWS= {Cx, Cy, Cz};
// 업로드 힙에 memcpy → SetGraphicsRootConstantBufferView(b0, ...)
cmdList->SetGraphicsRootConstantBufferView(0, objectCBAddress);
// 파이프라인 바인딩 후 사각형(인덱스 6) 드로우
cmdList->IASetPrimitiveTopology(D3D_PRIMITIVE_TOPOLOGY_TRIANGLELIST);
cmdList->IASetVertexBuffers(0, 1, &vbView);
cmdList->IASetIndexBuffer(&ibView);
cmdList->DrawIndexedInstanced(6, 1, 0, 0, 0);
C++
복사
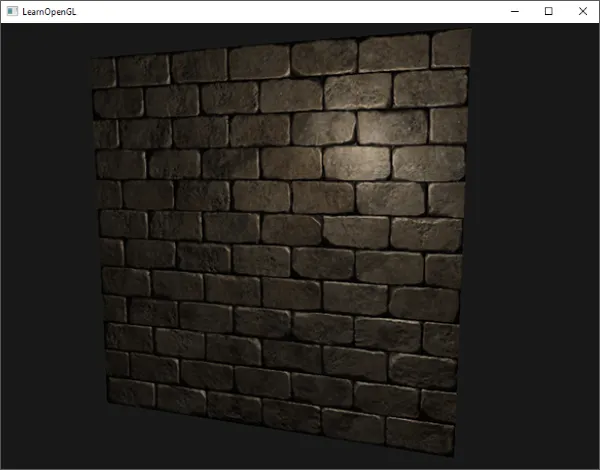
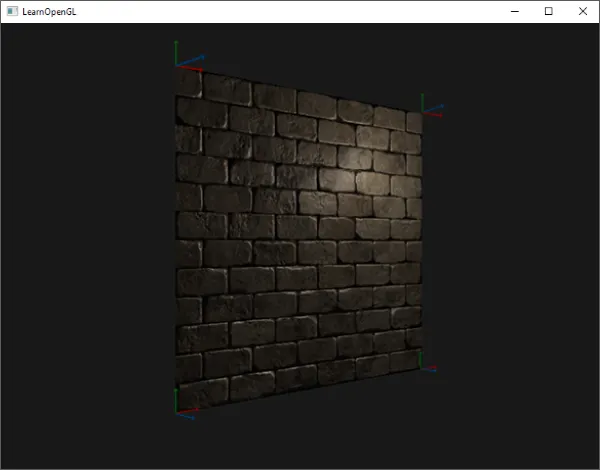
이는 실제로 올바른 노멀 매핑처럼 보인다:
탄젠트 공간 변환을 사용한 올바른 노멀 매핑
소스 코드는 여기에서 찾을 수 있다.
Complex objects
우리는 탄젠트 공간 변환과 함께 노멀 매핑을 사용하기 위해, 탄젠트와 비탄젠트 벡터를 수동으로 계산하는 방법을 보여주었다. 다행히도, 이러한 탄젠트와 비탄젠트 벡터를 수동으로 계산해야 하는 경우는 그리 자주 없다. 대부분의 경우 한 번 커스텀 모델 로더에 구현하거나, 우리 경우처럼 Assimp을 사용하는 모델 로더를 사용한다.
Assimp에는 모델을 로드할 때 설정할 수 있는 매우 유용한 구성 비트 aiProcess_CalcTangentSpace가 있다. 이 비트를 Assimp의 ReadFile 함수에 제공하면, Assimp은 이 장에서 우리가 했던 것과 유사하게 로드된 각 정점에 대해 부드러운(smooth) 탄젠트와 비탄젠트 벡터를 계산한다.
const aiScene *scene = importer.ReadFile(
path, aiProcess_Triangulate | aiProcess_FlipUVs | aiProcess_CalcTangentSpace
);
C++
복사
Assimp 내부에서는 다음과 같이 계산된 탄젠트를 가져올 수 있다:
Vector3 vector;
vector.x = mesh->mTangents[i].x;
vector.y = mesh->mTangents[i].y;
vector.z = mesh->mTangents[i].z;
vertex.Tangent = vector; // xyz, handedness는 별도 계산/저장
C++
복사
그다음 텍스처가 있는 모델에서 노멀 맵도 로드하도록 모델 로더를 업데이트해야 한다. Wavefront 객체 포맷(.obj)은 aiTextureType_NORMAL이 노멀 맵을 로드하지 않는 반면 aiTextureType_HEIGHT는 로드하는 등, Assimp의 규칙과 약간 다르게 노멀 맵을 내보낸다:
std::vector<Texture> normalMaps =
loadMaterialTextures(material, aiTextureType_HEIGHT, "texture_normal");
C++
복사
물론, 이는 로드된 모델과 파일 형식의 종류에 따라 달라진다.
업데이트된 모델 로더를 사용하여 스페큘러와 노멀 맵을 가진 모델에서 애플리케이션을 실행하면 다음과 같은 결과가 나온다:
Assimp로 로드한 복잡한 객체에 대한 노멀 매핑
보는 바와 같이, 노멀 매핑은 그리 많은 추가 비용 없이 객체의 디테일을 놀라울 정도로 끌어올린다.
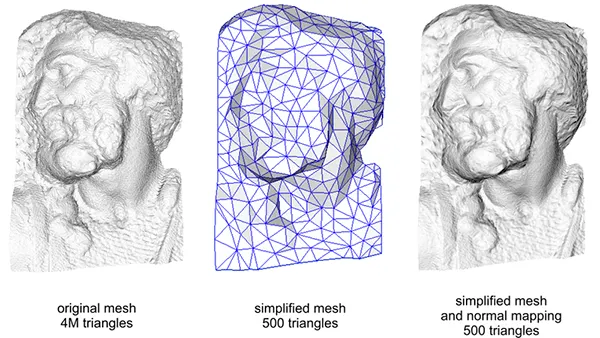
노멀 맵을 사용하는 것은 성능을 높이는 좋은 방법이기도 하다. 노멀 매핑 이전에는 메시의 높은 디테일을 얻기 위해 많은 수의 정점을 사용해야 했다. 노멀 매핑을 사용하면 훨씬 적은 정점으로 동일한 수준의 디테일을 메시에서 얻을 수 있다. 아래 Paolo Cignoni의 이미지는 두 방법을 멋지게 비교해 보여준다:
노멀 매핑 유무에 따른 메시 디테일 시각화 비교
고정점(정점 수가 많은) 메시와 노멀 매핑이 적용된 저정점 메시의 디테일은 거의 구분이 안 된다. 따라서 노멀 매핑은 보기 좋을 뿐 아니라, 많은(너무 많은) 디테일을 잃지 않으면서 고정점 메시를 저정점 메시로 대체하기 위한 훌륭한 도구다.
One last thing
그다지 많은 추가 비용 없이 품질을 약간 개선하는 마지막 요령이 하나 남아 있다.
상당한 수의 정점을 공유하는 더 큰 메시에서 탄젠트 벡터가 계산될 때, 일반적으로 보기 좋고 부드러운 결과를 위해 탄젠트 벡터가 평균화된다. 이 접근의 문제는 세 개의 TBN 벡터가 서로 수직이 아니게 끝날 수 있다는 점이며, 이는 결과 TBN 행렬이 더 이상 직교하지 않음을 의미한다. 비직교 TBN 행렬에서도 노멀 매핑은 약간만 어긋날 뿐이지만, 여전히 개선할 수 있는 부분이다.
Gram-Schmidt 과정이라고 하는 수학적 요령을 사용하면, 각 벡터가 다시 다른 벡터에 수직이 되도록 TBN 벡터를 재직교화(re-orthogonalize)할 수 있다. 정점 셰이더에서는 다음과 같이 한다:
// 비균일 스케일 시에는 inverse-transpose(3x3) 사용 권장
float3 N = normalize(mul(float4(vin.Normal, 0.0f), gWorld).xyz);
float3 T = normalize(mul(float4(vin.Tangent.xyz, 0.0f), gWorld).xyz);
// N에 대해 T를 재직교화
T = normalize(T - dot(T, N) * N);
// 그런 다음 T와 N의 외적으로 수직 벡터 B를 구함
float3 B = normalize(cross(N, T)) * vin.Tangent.w;
float3x3 TBN = float3x3(T, B, N);
GLSL
복사
이는 아주 약간이지만 일반적으로 노멀 매핑 결과를 조금의 추가 비용으로 개선해준다. 추가 리소스의 Normal Mapping Mathematics 비디오 마지막 부분을 보면 이 과정이 실제로 어떻게 작동하는지에 대한 훌륭한 설명을 볼 수 있다.
Additional resources
•
Tutorial 26: Normal Mapping: normal mapping tutorial by ogldev.
•
How Normal Mapping Works: a nice video tutorial of how normal mapping works by TheBennyBox.
•
Normal Mapping Mathematics: a similar video by TheBennyBox about the mathematics behind normal mapping.
•
Tutorial 13: Normal Mapping: normal mapping tutorial by opengl-tutorial.org.