PBR 1: 빛이란?
게임이나 3D 작업에서 'PBR'이라는 용어를 자주 접하게 됩니다. "이거 PBR 텍스처", "PBR 셰이더 적용" 같은 말들입니다. 하지만 "PBR이 정확히 무엇인가?"라고 물으면 복잡한 용어들로 인해 혼란스러울 수 있습니다.
이 글에서는 PBR에 대해 설명합니다. 프로그래머와 PBR을 처음 접하는 아티스트 모두를 위한 내용입니다.
PBR(Physically Based Rendering)은 "물리 기반 렌더링"을 의미합니다.
현실 세계에서 물체를 보고 빛을 인지하는 방식을 최대한 비슷하게 컴퓨터 그래픽으로 구현하는 기술입니다. 컴퓨터가 현실의 모든 물리 현상을 완벽하게 재현하는 것은 불가능합니다. 그러나 PBR은 기존 방식보다 훨씬 더 물리적으로 정확하고 사실적인 결과를 만들어내는 접근 방식입니다.
PBR을 공부하면 다음과 같은 용어들을 만나게 됩니다.
•
전역 조명 (Global Illumination)
•
에너지 보존 법칙 (Energy Conservation)
•
반사도 (Reflectivity), 디퓨즈, 스페큘러
•
미세면 (Microsurface), 러프니스
•
프레넬 법칙 (Fresnel's Law)
•
금속성 (Metalicity)
이 용어들이 어렵게 느껴질 수 있습니다. 특히 아티스트나 그래픽스를 처음 접하는 프로그래머에게는 부담스러울 수 있습니다.
이 모든 것을 한 번에 이해할 필요는 없습니다. PBR을 제대로 이해하려면 상당한 분량의 학습이 필요합니다.
이 글은 PBR을 시리즈로 나누어 설명합니다. 첫 번째로 PBR을 이해하기 위한 기본 요소인 빛이 무엇인지, 그리고 우리가 빛을 어떻게 인지하는지를 다룹니다.
 빛이란 무엇인가
빛이란 무엇인가
우리는 매일 빛을 경험하지만, "빛이 무엇인가?"라는 질문에 답하기는 쉽지 않습니다. 아인슈타인조차 "평생 빛이 무엇인지 고민했다"고 말했습니다.
PBR을 이해하기 위해 복잡한 물리학(양자론 등)을 모두 알 필요는 없습니다. 필요한 만큼만 알아보겠습니다.
빛은 전자기파(Electromagnetic wave)라고 불리는 에너지의 한 형태입니다. 파동처럼 에너지가 퍼져나가는 형태입니다.
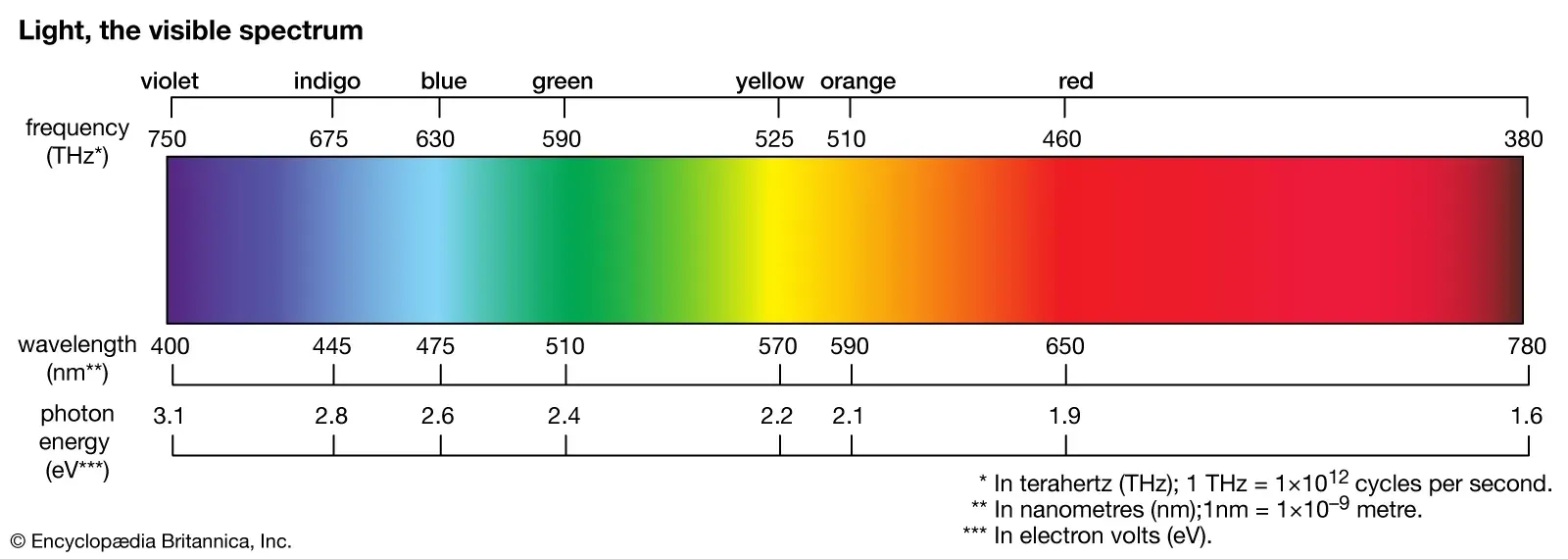
[그림1. 전자기파의 스펙트럼]
(이미지: 전자기파 스펙트럼 그래프. 감마선, X선, 자외선, 가시광선, 적외선, 마이크로파, 라디오파 등을 보여줌.)
전자기파에는 많은 종류가 있습니다. (그림 1)처럼 파장에 따라 감마선, X선, 자외선, 적외선, 라디오파 등으로 분류됩니다.
넓은 의미에서는 이 모든 것을 빛이라고 부르지만, 일상적으로 말하는 빛은 우리 눈으로 볼 수 있는 가시광선(Visible spectrum) 영역만을 의미합니다. 적외선(IR)이나 자외선(UV)도 전자기파이지만 우리 눈에는 보이지 않습니다.
빛은 단일한 덩어리가 아닙니다. 여러 파장의 전자기파가 섞여 있는 조합입니다.
가장 대표적인 증거는 무지개입니다. 
[그림2. 프리즘을 통과하며 분리되는 빛]
(이미지: 백색광이 프리즘을 통과하며 여러 색(무지개)으로 나뉘는 모습.)
(그림 2)처럼 빛이 프리즘을 통과하면 여러 색으로 분리됩니다. 하나의 빛에 섞여 있던 여러 파장이 파장 길이에 따라 굴절률이 달라서 분리되는 현상입니다.
빨간색 계열이 가장 파장이 길고, 보라색 계열이 가장 파장이 짧습니다.
핵심은 "빛은 단일 색이 아니라 여러 파장의 조합"이라는 점입니다.
 우리는 빛을 어떻게 인지하는가
우리는 빛을 어떻게 인지하는가
여러 파장이 섞인 전자기파를 우리 눈은 어떻게 색과 밝기로 인지하는가?
[그림 (a) 눈의 구조, (b) 망막의 상세 구조]
(이미지: (a) 인간 눈의 단면도, (b) 망막을 확대한 그림.)
빛이 우리 눈에 들어오면, (그림 a)처럼 각막과 수정체를 거쳐 망막(Retina)에 도달합니다. 망막은 카메라의 필름이나 이미지 센서 역할을 합니다.
(그림 b)처럼 망막에는 빛을 감지하는 두 종류의 세포가 있습니다.
1.
간상세포 (Rod cell)
•
명암을 감지합니다.
•
약한 빛에도 반응하여 어두운 곳에서 사물을 구분하게 합니다.
•
원추세포보다 수가 많습니다 (약 9,000만 개). 인간의 눈은 색 변화보다 밝기 변화에 더 민감합니다.
2.
원추세포 (Cone cell)
•
색상을 감지합니다.
•
3가지 종류가 있습니다: 빨간색(R) 빛에 민감한 세포, 초록색(G) 빛에 민감한 세포, 파란색(B) 빛에 민감한 세포 (약 600만 개).
R, G, B입니다.
포토샵, 유니티, 언리얼 엔진에서 색을 표현할 때 RGB(빛의 3원색) 값을 사용하는 이유가 여기에 있습니다. 우리 눈이 세상을 RGB 세 가지 색상의 조합으로 인지하기 때문에, 컴퓨터 화면도 RGB 빛을 조합하여 모든 색을 표현합니다.
이 RGB 시스템은 인간 중심적입니다.
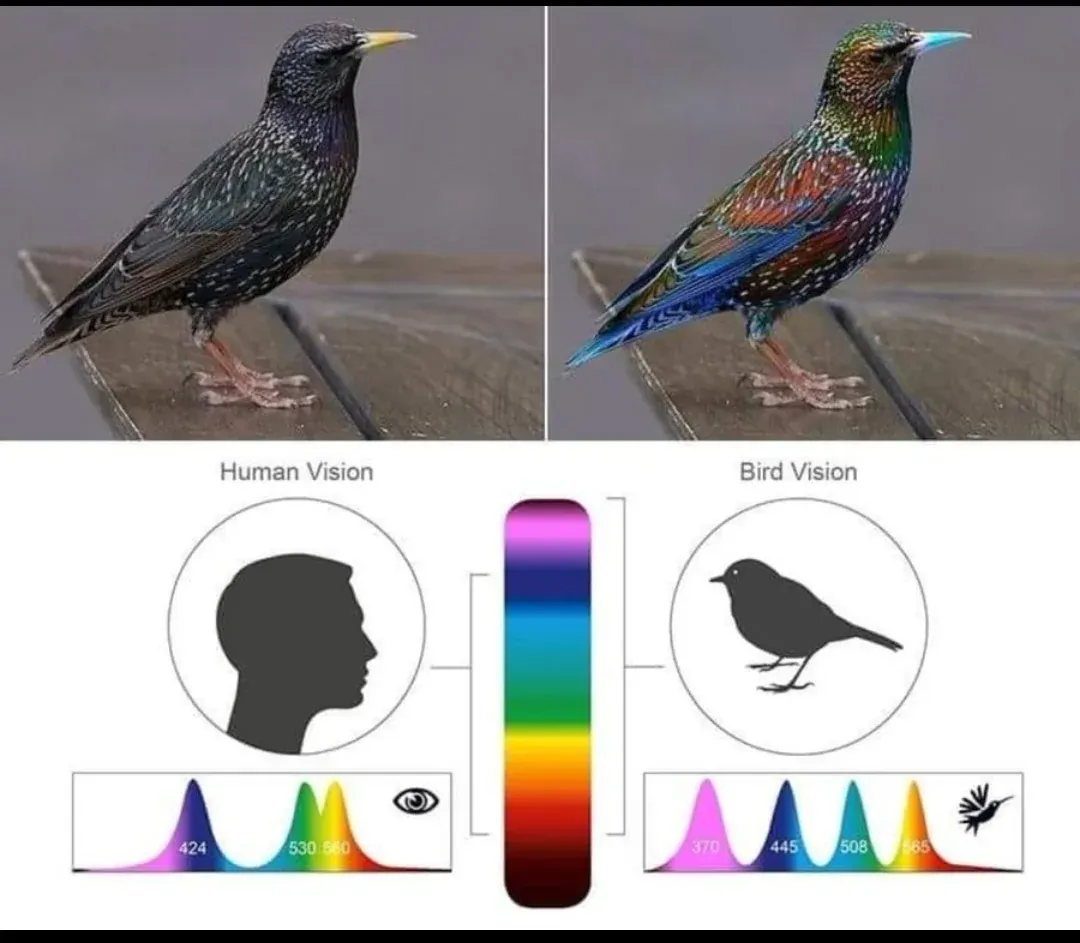
[그림4. 인간과 새가 인지하는 파장 비교]
대부분의 포유류는 인간(3종류)보다 적은 수의 원추세포(보통 2종류)를 가지고 있습니다. 새들은 (그림 4)처럼 4종류의 원추세포를 가지고 있으며, 인간이 볼 수 없는 자외선(UV) 영역까지 봅니다. 
[그림5. 인간과 새가 보는 색상의 차이]
(그림 5)처럼 우리 눈에는 노란색 꽃과 나비가 비슷하게 보이지만, 자외선을 보는 새의 눈에는 꽃과 나비의 자외선 무늬가 명확히 다르게 보입니다.
(참고: 인간의 원추세포는 녹색 파장에서 가장 민감하게 반응합니다. 이는 과거 숲에서 생존하기 위해 녹색을 잘 구분하도록 진화한 결과일 수 있습니다.  )
)
정리
1.
PBR은 물리 기반 렌더링의 약자로, 현실 세계의 빛을 최대한 유사하게 구현하는 그래픽 기술입니다.
2.
빛은 전자기파의 한 형태이며, 우리 눈은 그중 가시광선만 볼 수 있습니다.
3.
빛은 단색이 아니라 프리즘이 보여주듯 여러 파장의 조합입니다.
4.
우리 눈의 망막에는 원추세포가 있으며, 이것이 RGB (빨강, 초록, 파랑) 3가지 빛에 반응하여 모든 색을 인식합니다.
5.
컴퓨터 그래픽에서 RGB를 사용하는 것은 우리 눈이 세상을 보는 방식을 따른 것입니다.
오늘은 PBR의 핵심 요소인 빛과 우리의 시각에 대해 다뤘습니다. RGB를 사용하는 근본적인 이유를 이해했습니다.
PBR 2: 조도와 휘도
개요
그래픽스에서 "Radiance", "Irradiance", "Luminance", "Illuminance"라는 용어는 혼란을 유발합니다. Radiance와 Luminance가 혼용되는 경우가 많기 때문입니다.
•
Radiance: 복사 휘도
•
Irradiance: 복사 조도
•
Luminance: 휘도
•
Illuminance: 조도
이 문서의 목적은 이 용어들의 차이를 명확히 정의하는 것입니다.
방사측정 (Radiometry) vs. 광도측정 (Photometry)
우리는 빛이 다양한 전기파로 이루어진걸 알 수있었습니다. 에너지가 입자나 파동형태로 전달되거나 방출되는 것을 방사선(radiation)이라고 합니다. 즉 가시 광선을 포함한 전체 파장 영역의 전자기파들로 구성 된 빛을 방사선 이라고 부릅니다. 넓읜 의미의 빛(빛의 전체 영역)을 다루기 위해 이 에너지를 측정하는 것을 방사 측정(radiometry)라고 합니다. 그리고 좁은 의미(가시영역)을 측정하는 것을 광도측정 ( Photometry )라고 합니다.
이 용어들은 측정하는 빛의 범위에 따라 구분됩니다.
1.
방사측정 (Radiometry)
•
대상: 가시광선을 포함한 모든 파장 영역의 전자기파. 자외선, 적외선 등 눈에 보이지 않는 에너지까지 모두 측정합니다.
•
단위: 물리적 에너지를 측정하며 와트(W/m²) 등을 사용합니다.
•
용어: Radiance, Irradiance
1.
광도측정 (Photometry)
•
대상: 인간의 눈에 보이는 가시광선 영역만 측정합니다.
•
단위: 인간이 인지하는 '밝기'를 측정하며 루멘(lumen) 또는 **럭스(lux)**를 사용합니다.
•
용어: Luminance, Illuminance
컴퓨터 그래픽스는 최종적으로 인간의 눈으로 보는 결과물을 만듭니다. 따라서 보이지 않는 영역의 에너지를 계산할 필요가 없으므로, 광도측정(Photometry) 관점을 기본으로 합니다.
결론: 그래픽스 분야에서는 다음과 같이 이해해도 무방합니다.
•
Radiance ≈ Luminance (휘도)
•
Irradiance ≈ Illuminance (조도)
조도의 "조( 照 )"는 "비출 조" 입니다. 그리고 휘도의 "휘( 輝 )"는 "빛날 휘"입니다. 조는 능동적인 표현이고 휘는 수동적인 표현입니다. 빛을 생각할 때 광원에서 빛이 나오는 것을 "비춘다"라고 표현하고, 어딘가 부딪혀서 눈에 들어 오는 것을 "빛난다" 라고 표현하는 것입니다.
Irradiance (복사 조도)
•
광원(태양 등)에서 나온 모든 파장의 복사 에너지가 특정 표면에 도달하는 양(밀도)을 의미합니다.
•
어떤 면이 받는(비추는) 총 에너지의 양입니다.
•
방향과 관계없이 특정 지점의 표면이 얼마나 많은 에너지를 받는지만 측정합니다.
•
예: 지구 대기권 밖에서 태양으로부터 단위 면적당 받는 총 에너지(자외선, 가시광선, 적외선 등 모두 포함).
Radiance (복사 휘도)
•
물체 표면에서 반사(또는 방출)되어 특정 방향으로 나아가는 모든 파장의 복사 에너지의 양(세기)을 의미합니다.
•
관찰자(카메라, 센서)가 특정 방향에서 '바라보는' 물체의 총 에너지 세기입니다.
•
방향에 따라 값이 달라지는 것이 핵심입니다.
•
예: 뜨겁게 달궈진 쇠공 표면에서 특정 방향(예: 관찰자의 눈)으로 방출되는 총 에너지(눈에 보이는 붉은빛과 보이지 않는 적외선(열)을 모두 포함).
조도 (Illuminance) vs. 휘도 (Luminance) version
조도와 휘도를 구분하는 이유
물체 표면에 도달한 빛(조도)이 100% 우리 눈으로 반사(휘도)되지 않기 때문입니다.
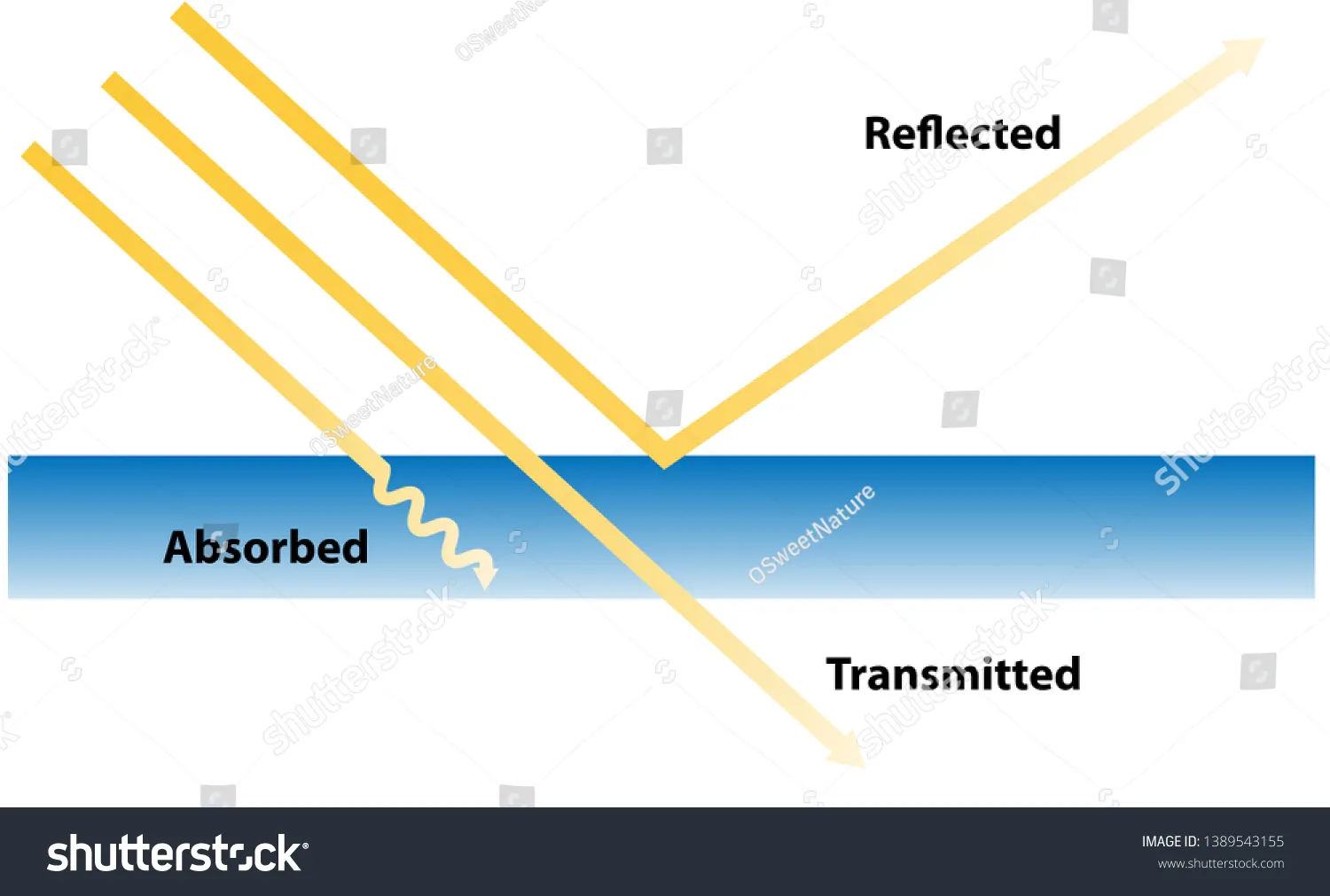
표면에 입사한(incident) 빛은 재질(매질)에 따라 다음과 같이 나뉩니다.
1.
흡수 (Absorbed): 빛 에너지가 재질 내부에 흡수됩니다. (예: 검은색 물체)
2.
투과 (Transmitted): 빛이 재질을 통과합니다. (예: 유리, 물)
3.
반사 (Reflected): 빛이 표면에서 튕겨 나옵니다. (예: 거울, 흰 종이)
인간의 눈은 이 중 '반사(Reflected)'된 빛만을 인지하여 물체의 색상과 밝기를 판단합니다. 따라서 PBR은 '표면에 닿는 빛(조도)'과 '반사되어 보이는 빛(휘도)'을 명확히 구분하여 계산해야 합니다.
정리
1.
Radiometry (Radiance/Irradiance): 모든 파장(자외선 포함)의 물리적 에너지를 측정.
2.
Photometry (Luminance/Illuminance): 인간의 눈에 보이는 가시광선의 밝기를 측정.
3.
그래픽스: Photometry 관점을 사용하므로 Radiance ≈ Luminance로 간주해도 무방.
4.
조도 (Illuminance): 표면에 도달하는 빛의 양. (Input)
5.
휘도 (Luminance): 표면에서 반사되어 눈에 들어오는 빛의 양. (Output)
6.
이유: 빛은 재질에 따라 흡수, 투과, 반사되며, 우리는 '반사'된 빛(휘도)만 볼 수 있기 때문.
PBR3. 빛의 감쇠
1. 개요: 물리 기반 단위의 필요성
전 단원에서 조도와 휘도, 방사 측정, 광도 측정의 차이에 대해서 이야기 했습니다.
PBR(물리 기반 렌더링)은 물리적으로 납득할 수 있는 기준과 단위를 필요로 합니다.
•
엔진 표준: UE4를 비롯한 최신 PBR 엔진들은 광원의 세기(Intensity) 단위로 **루멘(lumen)**을 사용하는 추세입니다.
•
이유: 아티스트가 임의의 값(기분)이 아닌, 물리적 표준에 따라 라이팅을 설정하도록 하기 위함입니다.
•
목표: 이 글은 루멘과 같은 광학 단위들을 이해하기 위한 선행 학습으로, 빛이 물리적으로 어떻게 약해지는지(감쇠)를 다룹니다.
2. 빛의 감쇠 원리: 거리와 밀도
빛은 멀어질수록 약해집니다. 이는 빛 에너지가 사라져서가 아니라(감쇄, Attenuation), 퍼지기(Density) 때문입니다.
•
빛의 입자성: 빛을 **광자(Photon)**라는 입자로 가정합니다. 진공에서 광자는 산란이나 흡수 없이 직진합니다.
•
광원 비교:
◦
태양광 (Directional Light): 태양은 매우 멀리 있기 때문에, 지구에 도달하는 광자들은 거의 평행하다고 가정합니다. 이 때문에 그래픽스에서는 거리 감쇠를 적용하지 않습니다.
◦
포인트/스포트 라이트 (Point/Spot Light): 광원과 물체가 가깝습니다. 광자가 모든 방향으로 퍼져나가며, 각도의 차이가 커집니다.
•
감쇠의 핵심 원리:
◦
광원에서 방출되는 광자의 총 개수는 동일합니다.
◦
광원으로부터 거리가 멀어질수록, 이 동일한 개수의 광자가 더 넓은 면적을 덮어야 합니다.
◦
결과적으로 **단위 면적당 광자의 밀도(Density)**가 줄어들고, 이것이 우리가 '어둡다'고 인지하는 감쇠 현상입니다.
3. 감쇠의 계산: 거리 제곱의 역수 법칙
앞에서 포인트/스포트 라이트와 Directional Light의 차이는 그냥 거리의 차이 였습니다. 빛을 받는 오브젝트들은 거리가 너무 가깝기 때문에 작은 각도의 차이가 크게 변화를 줍니다. 태양광은 엄청나게 많은 광자를 내뿜고 있고 그 거리가 매우 멀기 때문에 거의 완전하게 빛이 평행하게 들어온다고 가정했습니다. 그래서 우리는 태양광에서는 감쇠를 설정하지 않았습니다.
빛을 2차원 평면으로 두고 보았을 때 빛의 발생 진원지에서 나오는 광자의 갯수는 똑같습니다. 빛이 평행하기 움직이면서 거리가 멀어질 수록 각 광자 사이의 거리는 멀어집니다. 그래서 빛의 밀도가 약해진다고 볼 수 있습니다.
이 '밀도'가 줄어드는 방식을 수학적으로 증명하기 위해 입체각(Solid Angle) 개념이 필요합니다.
입체각(Solid Angle) 개념이 필요한 이유는 빛이 3차원 공간에서 퍼져나가는 면적을 정확히 계산하기 위해서입니다.
구체적으로:
•
2D에서는 호도법으로 충분: 평면에서 각도를 표현할 때는 호도법(Radian)만 있어도 호의 길이를 쉽게 계산할 수 있습니다.
•
3D에서는 입체각이 필요: 광원에서 나온 빛은 3차원 공간의 구 표면으로 퍼져나갑니다. 이때 빛이 덮는 면적을 계산하려면 입체각이 필요합니다.
•
감쇠 법칙 증명의 핵심: 입체각이 일정할 때, 거리가 멀어지면 빛이 덮는 면적이 r²에 비례해서 커진다는 것을 수학적으로 보여줄 수 있습니다.이것이 바로 거리 제곱의 역수 법칙의 근거가 됩니다.
결국 입체각 없이는 "왜 면적이 거리의 제곱에 비례하는가?"를 엄밀하게 설명할 수 없습니다.
호도법 (Radian, 2D)
•
도(Degree): 360° 기반. 호의 길이 계산이 복잡합니다.
•
호도(Radian): 2π 기반. 각을 '반지름 대비 호의 길이'로 정의합니다.
•
정의: 반지름 r일 때 호의 길이가 r이 되는 각 = 1 rad
•
공식: 호의 길이 = 반지름(r) × 중심각(rad)
입체각 (Solid Angle, 3D)
•
3D 공간에서의 각도입니다.
•
정의: 반지름 r인 구(Sphere)에서 겉넓이가 r²이 되는 면적을 포함하는 원뿔형의 각 = 1 스테라디안(sr)
steradian
radian
•
공식: 겉넓이(A) = 반지름(r)² × 입체각(a)
•
(참고: 구 전체의 겉넓이는 4πr²이므로, 구 전체의 입체각은 4π sr입니다.)
감쇠 증명 (Inverse Square Law)
1.
광원이 고정된 **입체각(a)**으로 빛(광자)을 방출한다고 가정합니다. 이 입체각 a는 거리에 상관없이 일정합니다.
2.
빛이 도달하는 면적은 겉넓이 = r² × a 공식을 따릅니다.
3.
거리가 2배가 되면(r=2), 면적은 (2r)² = 4배가 됩니다.
4.
거리가 3배가 되면(r=3), 면적은 (3r)² = 9배가 됩니다.
5.
즉, 빛이 덮어야 할 면적은 거리(Distance)의 제곱에 비례하여 커집니다.
6.
동일한 양의 빛이 Distance²배 넓은 면적에 퍼지므로, 빛의 세기(밀도)는 거리의 제곱에 반비례하여 약해집니다.
Intensity ∝ 1 / Distance²
4. 엔진에서의 실용적 적용: 감쇠 반경
수학적으로 1 / Distance²는 거리가 무한대가 되어도 0이 되지 않습니다.
•
문제점: 씬의 모든 오브젝트가 모든 광원의 영향을 받는다고 계산하면, 거의 보이지도 않는 빛 때문에 엄청난 연산 비용이 발생합니다.
•
해결책: "감쇠 반경 (Attenuation Radius)"
◦
아티스트가 광원의 최대 영향력 거리를 수동으로 설정하는 값입니다.
◦
이 반경을 벗어난 물체는 해당 광원의 계산에서 제외됩니다.
◦
이는 물리적 정확도(빛은 0이 안 됨)와 성능(계산 비용 절감) 사이의 실용적인 타협입니다.
•
용어 주의: 'Attenuation Radius'(영향 범위)와 'Source Radius'(Area Light의 광원 크기)를 혼동해서는 안 됩니다.
5. 정리
•
빛의 감쇠는 에너지가 사라지는 것이 아니라, 광자의 밀도가 낮아지는 현상입니다.
•
광자가 퍼지는 면적은 **입체각(Solid Angle)**의 정의에 따라 **거리의 제곱(r²)**에 비례하여 증가합니다.
•
따라서 빛의 세기는 **거리의 제곱에 반비례(1/r²)**하여 감쇠합니다.
•
엔진은 성능을 위해 **'감쇠 반경'**을 두어, 특정 거리 밖의 조명 계산을 강제로 0으로 처리합니다.
PBR4. 광원의 밝기(광속)
지난 시간 [빛의 감쇠] 편에서 PBR의 밑바탕이 되는 지루한 수학과 기하학(거리, 호도법, 입체각)에 대해 이야기했습니다. 이는 **'빛의 측정 단위'**를 이해하는 데 필수적인 재료가 됩니다.
오늘도 미리 말씀드리지만, 우리는 '방사측정(Radiometry)'이 아닌 '광도측정(Photometry)' 관점에서 빛을 다룰 거예요. 즉, 눈에 보이는 **'가시광선'의 '밝기'**에 대해 이야기하는 거죠.
조금 어렵게 느껴지는 수식들이 등장할 수도 있지만, 원리만 이해하면 크게 어렵지 않습니다.
1.  광선속 (광속, Luminous Flux, Luminous Power)
광선속 (광속, Luminous Flux, Luminous Power)
여기서 말하는 '광속'은 '빛의 속도(光速)'가 아닙니다.
한자로는 '빛 광(光)', '묶을 속(束)'을 써서 '빛다발'을 의미합니다. 영어로는 'luminous(빛나는)', 'flux(흐름)'이므로, '빛의 흐름' 또는 '빛다발'이라고 이해하면 됩니다.
광속이란?
광원에서 단위 시간당 방출하는 가시광선의 총량입니다.
[그림1. 광속은 광원에서 나오는 빛의 총량입니다.]
(이미지: 전구에서 모든 방향으로 빛이 퍼져나가는 모습과 'Luminous Flux'라고 표시된 다이어그램)
전구를 보고 "이 전구의 밝기는 1000루멘이다"라고 말할 때 사용하는 것이 바로 이 '광속'입니다.
전구 회사 제품의 사양에 표시된 Luminous Flux(lm)
•
단위: 루멘 (lumen, lm)
◦
'루멘'은 라틴어로 '빛'이라는 뜻입니다.
•
왜 와트(W) 대신 루멘(lm)을 사용하는가?
◦
과거에는 조명의 밝기를 와트(W)로 많이 표기했습니다. 하지만 와트(W)는 에너지 소비량을 나타내는 단위일 뿐, 밝기를 의미하지는 않습니다.
◦
LED 조명처럼 적은 와트(W)로도 밝은 빛(루멘)을 낼 수 있는 조명이 등장하면서, 이제 조명의 밝기는 루멘(lm)으로 표기하는 것이 표준이 되었습니다.
2.  광도 (Luminous Intensity)와 칸델라 (Candela)
광도 (Luminous Intensity)와 칸델라 (Candela)
그렇다면 이 '루멘'은 어떻게 결정되는 것일까요?
오래전부터 사람들은 촛불을 사용해 빛을 밝혔습니다. 과학자들은 촛불을 기준으로 빛의 밝기를 측정하려 했습니다.
하지만 촛불처럼 모든 방향으로 빛이 나가는 광원도 있지만, LED처럼 특정 방향으로만 빛이 나가는 광원도 있습니다. 측정기를 광원 전체를 완벽하게 둘러싸도록 만들기는 어렵기 때문에, 특정 영역만큼만 측정한 값으로 전체를 추정하는 경우가 많습니다.
이런 문제 때문에 과학자들은 '모든 방향'이 아닌 '특정 방향'으로 나오는 빛의 양을 기준으로 삼는 방법을 고안했습니다. 이때 핵심이 되는 개념이 바로 지난 시간에 배웠던 '입체각 (Solid Angle)'입니다.
[  잠깐 복습: 1 스테라디안 (sr) ]반지름 r인 구(Sphere)에서, 겉넓이가 r²이 되는 면적을 포함하는 원뿔형의 3차원 각도를 1 스테라디안(sr)이라고 부릅니다.[그림2. 1 스테라디안]
(이미지: 구의 중심에서 원뿔형으로 퍼져나가는 입체각과 구의 표면에 생기는 면적 A(r^2)를 보여주는 그림.)
잠깐 복습: 1 스테라디안 (sr) ]반지름 r인 구(Sphere)에서, 겉넓이가 r²이 되는 면적을 포함하는 원뿔형의 3차원 각도를 1 스테라디안(sr)이라고 부릅니다.[그림2. 1 스테라디안]
(이미지: 구의 중심에서 원뿔형으로 퍼져나가는 입체각과 구의 표면에 생기는 면적 A(r^2)를 보여주는 그림.)
이 '1 스테라디안'을 기준으로 삼아서, 다음과 같이 '광도'를 정의했습니다.
광도 (Luminous Intensity)란?점 광원에서 특정 방향으로 '단위 입체각 (1 스테라디안)'당 방출되는 광속입니다.
•
단위: 칸델라 (candela, cd)
[그림3. 광도(Luminous Intensity) 칸델라]
(이미지: 광원에서 특정 방향으로 원뿔형의 1스테라디안 입체각을 통해 빛이 방출되는 그림과 'Luminous Intensity', 'Candela' 표시.)
이를 수식으로 표현하면 다음과 같습니다:
만약 점광원처럼 빛이 모든 방향으로 균일하게 방출된다면, 구 전체의 최대 입체각은 스테라디안이므로, 광도(칸델라)는 다음과 같이 계산할 수 있습니다.
3. 다시, 루멘 (Lumen)의 정의
광도(칸델라)를 이해했으니, 이제 '루멘(광속)'을 좀 더 명확하게 정의할 수 있습니다.
광속은 다음과 같이 정의됩니다.
만약 1 칸델라의 광도를 가진 빛이 1 스테라디안의 입체각으로 방출된다면, 그 빛의 양이 바로 1 루멘(lm)이 됩니다.
이를 통해 점광원의 광속을 계산하면 다음과 같습니다.
4. 칸델라와 루멘의 기준 (역사적 배경 추측)
여기서 헷갈릴 수 있습니다. "광속은 칸델라로 정의되고, 칸델라는 또 광속으로 정의되는 것 아닌가?" 하고요. 자료를 찾기가 쉽지 않지만, 추측을 섞어 설명해보겠습니다.
아마 과학자들은 처음에는 '촛불 하나'를 1 루멘이라고 불렀을 것입니다. 하지만 '모든 방향으로 빛이 나가지 않는 광원'이 생기면서, 전체 빛의 양을 기준으로 삼는 것이 어려워졌을 것입니다.
그래서 '특정 방향으로, 단위 입체각(1 스테라디안) 안에서 방출되는 빛의 양'을 새로운 기본 단위인 '광도(luminous intensity)'로 삼고, 이를 '1 칸델라(cd)'라고 정했을 것입니다. '1 칸델라'는 리터나 그램처럼 국제 표준으로 정해져 있는 빛의 양입니다.
이 '1 칸델라'를 기준으로 촛불의 광속(루멘)을 계산해보겠습니다.
촛불 하나가 모든 방향( 스테라디안)으로 1 칸델라의 광도로 빛을 방출한다고 가정하면:
실제로 촛불 하나의 광속은 약 12.57 루멘입니다. 이렇게 1 칸델라라는 기준을 먼저 세워두니, 다른 광원들의 루멘 값도 정확하게 계산할 수 있게 됩니다.
5. 정리
•
광속 (Luminous Flux, lm): 광원에서 나오는 가시광선의 총량 (얼마나 많은 빛이 나오는가).
•
광도 (Luminous Intensity, cd): 광원에서 특정 방향, 단위 입체각(1 스테라디안)당 방출되는 광속 (특정 방향으로 얼마나 강하게 빛이 나가는가).
•
관계:
◦
1 칸델라의 광도로 1 스테라디안의 입체각으로 방출되는 빛의 양이 바로 1 루멘입니다.
◦
광속 = 광도 × 입체각
◦
광도 = 광속 / 입체각
이 개념들을 이해하면 PBR 엔진에서 조명의 '세기(intensity)'를 조절할 때, 단순히 숫자만 입력하는 것이 아니라 물리적으로 어떤 의미를 가지는지 파악하는 데 도움이 됩니다.
다음 시간에는 이 개념들을 바탕으로 실제 조명들이 어떻게 작동하고, PBR에서는 어떻게 활용되는지 더 자세히 알아보겠습니다.
PBR5. 조도(Illuminance) 측정
1.  조도(Illuminance)의 정의
조도(Illuminance)의 정의
•
*조도(Illuminance)**는 조명이 비추는 빛이 특정 표면에 얼마나 많이 도달했는지를 측정한 값입니다.
지난 [4. 광원의 밝기(광속)]에서 배운 광속(Luminous Flux) 개념을 사용해 정의할 수 있습니다.
정의: 조도는 **단위 면적(m²)당 도달하는 광속(lumen)**입니다.
단위: 럭스(lux, lx)
쉽게 말해, 1평방미터()의 면적에 1루멘(l)의 빛다발이 도달할 때, 그 표면의 조도를 **1럭스()**라고 합니다.
2.  조도 계산의 변수: 거리와 기울기
조도 계산의 변수: 거리와 기울기
하지만 실제 세계에서 조도는 위 공식처럼 단순하지 않습니다. 빛이 1미터 거리에서 수직으로 비추는 경우는 거의 없기 때문입니다. 조도를 계산할 때는 다음 두 가지 핵심 요소를 반드시 고려해야 합니다.
① 거리 (빛의 감쇠)
우리는 [3. 빛의 감쇠]에서 빛의 세기가 **거리의 제곱에 반비례()**하여 약해진다는 것을 배웠습니다.
•
이유: 광원(점광원)에서 나온 빛은 거리가 멀어질수록 더 넓은 면적을 덮어야 합니다.
•
결과: 동일한 양의 빛(광자)이 더 넓은 영역으로 퍼지기 때문에, 단위 면적당 도달하는 빛의 밀도(조도)는 그 거리의 제곱만큼 약해집니다.
•
예시: 거리가 2배 멀어지면 빛이 덮는 면적은 4배()가 되고, 조도는 로 줄어듭니다.
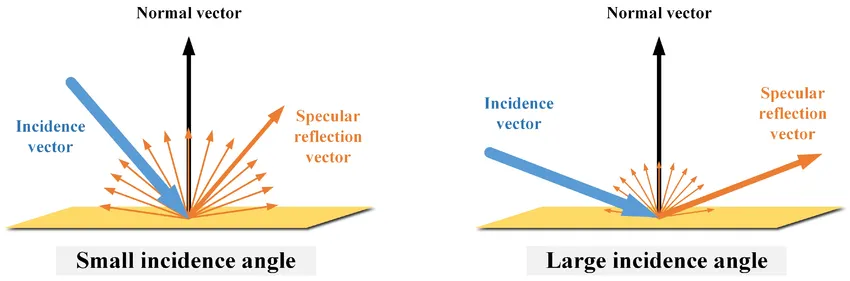
② 기울기 (램버트 코사인 법칙)
실세계의 물체 표면은 대부분 광원을 정면으로 마주 보지 않고 기울어져 있습니다.
•
현상: 표면이 광원을 기준으로 기울어져 있을수록, 같은 면적이라도 받아들이는 빛의 양이 줄어듭니다.
•
이유: 같은 빛다발이라도 기울어진 표면에는 더 넓게 퍼져서 닿기 때문에, 단위 면적당 밀도가 낮아집니다.
•
법칙: 이렇게 표면의 기울기(법선 벡터와 빛 벡터의 각도)에 따라 조도가 변하는 것을 계산하는 법칙이 **램버트 코사인 법칙(Lambert's Cosine Law)**입니다.
3.  예외: 태양광
예외: 태양광
태양광(Directional Light)은 이 규칙의 중요한 예외입니다.
•
가정: 태양은 지구에서 너무 멀리 떨어져 있기 때문에, 지구에 도달하는 모든 빛은 평행하게 들어온다고 가정합니다.
•
차이점:
◦
점광원의 빛이 감쇠하는 이유는 거리가 멀어질수록 '퍼져서(면적이 넓어져서)'입니다.
◦
태양광은 평행하게 들어온다고 가정하므로, 거리가 멀어져도 빛이 퍼지지 않아 커버해야 할 면적에 변화가 없습니다.
•
결론: 태양광은 거리에 따른 빛의 감쇠()를 적용하지 않습니다. (단, 기울기에 따른 램버트 코사인 법칙은 동일하게 적용됩니다.)
4. 정리
1.
조도(Illuminance): 표면에 도달한 빛의 양. 단위는 **럭스(lux)**입니다. ()
2.
거리: 점광원/스포트라이트는 **거리 제곱의 역수()**로 조도가 감쇠합니다.
3.
기울기: 표면의 기울기에 따라 램버트 코사인 법칙으로 조도가 감쇠합니다.
4.
태양광: 평행광으로 가정하므로, 거리에 따른 감쇠는 적용하지 않습니다.
PBR6. 휘도(Luminance)
이번 장에서는 빛의 여정에서 마지막 단계인 휘도(Luminance) 측정을 다룬다. 광원에서 출발하여 표면에 도달한 빛이 최종적으로 우리 눈에 어떻게 인식되는지 살펴본다.
1. 휘도(Luminance)란?
[그림1. 조도와 휘도의 관계]
(이미지: 광원에서 나온 빛이 표면에 닿는 '조도'와, 표면에서 반사되어 눈으로 들어오는 '휘도'의 관계를 보여주는 다이어그램)
앞서 설명한 바와 같이, 조도는 표면에 도달하는 빛의 양이고, 휘도는 우리 눈에 들어오는 빛의 양이다. 인간은 눈에 들어온 빛만을 인지할 수 있기 때문에, 휘도는 시각적 인식에 있어 가장 중요한 개념이다.
휘도(Luminance)란?특정 표면에서 방출되거나 반사되어 특정 방향으로, 단위 면적당, 단위 입체각 내로 들어오는 빛의 양(광도)을 측정한다.
•
단위: 제곱미터당 칸델라 ()
즉, 특정 표면의 특정 지점에서 반사된 빛이 특정 방향(예: 관측자의 눈)으로 얼마나 강하게 들어오는가를 측정하는 값이다.
2. 미세 표면(Micro-surface)과 핀홀 카메라(Pin-hole Camera) 모델
실제 그래픽스 계산을 위해서는 개념을 단순화할 필요가 있다.
① 거대 표면(Macro-surface)과 미세 표면(Micro-facet)
•
표면(Macro-surface): 인지 가능한 최소 단위의 작은 면적을 가진 표면. PBR 이전에는 이 거대 표면을 중심으로 라이팅을 계산했다.
•
미세 표면(Micro-surface / Micro-facet): 거대 표면보다 훨씬 작은, 눈에 보이지 않는 미세한 표면. PBR에서는 이 미세 표면의 거칠기까지 고려한다.
거대 표면조차도 점처럼 인식될 수 있으며, 이 관점에서 보면 표면에 들어오는 빛은 선에 가깝게 표현된다. 이러한 단순화는 조도와 휘도의 관계를 명확하게 한다.
② 핀홀 카메라 모델(Pin-hole Camera Model)
실시간 그래픽스에서는 눈을 바늘구멍(핀홀)처럼 아주 작은 구멍 하나만 있는 카메라로 가정한다.
[그림4. 핀홀 카메라 모델]
(이미지: 아주 작은 구멍을 통해 빛이 들어와 한 점에 모이는 핀홀 카메라의 원리)
•
가정: 모든 빛은 이 바늘구멍이라는 한 점으로 수렴한다.
•
결과: 눈으로 들어오는 빛은 선으로 표현될 수 있다.
결과적으로, 실시간 그래픽스 이론에서는 점에 가까운 표면과 핀홀 카메라(점 눈)가 상호작용하는 모델을 사용한다.
3. 조도와 휘도의 구분
PBR의 핵심 원리를 이해하기 위한 중요한 질문이다.
표면에 들어온 빛(조도)이 모두 우리 눈에 들어오는 빛(휘도)이 되는 것은 아니다.
모든 표면은 빛을 만나면 3가지 운명 중 하나를 결정한다.
1.
흡수(Absorption): 빛 에너지를 흡수하여 소멸시킨다. (예: 검은색 물체)
2.
반사(Reflection): 빛을 튕겨내 관측자의 눈이나 다른 곳으로 보낸다. (예: 거울, 불투명한 물체)
3.
투과(Transmission): 빛을 통과시켜 재질을 가로질러 반대편으로 보낸다. (예: 유리, 물)
(이미지: 표면에 빛이 들어와 반사(BRDF)되거나 투과(BTDF)되는 과정을 보여주는 다이어그램.)
[그림6. BRDF와 BTDF]
관측 가능한 빛은 오직 반사(Reflection)되거나 투과(Transmission)된 빛뿐이다. 따라서 조도와 휘도의 구분은 필수적이다.
•
PBR의 핵심: 얼마만큼의 빛이 반사되고 투과될지, 그리고 어떤 방식으로 분포될지를 물리적으로 정확하게 계산하는 것이다.
•
관련 이론: Albedo(표면 반사율), BRDF(양방향 반사 분포 함수), BTDF(양방향 투과 분포 함수) 등은 모두 표면에 들어온 빛이 얼마나 반사되고 투과되는지를 함수로 표현한 것이다.
4. 정리
지금까지 빛의 근본적인 개념부터 측정 방법, 그리고 표면과 눈에 도달하는 과정까지 다루었다. 이 모든 용어와 개념들은 앞으로 PBR의 핵심을 이해하는 데 지속적으로 등장한다.
다음부터는 본격적인 PBR 렌더링 구현을 다룬다. 실제 렌더링 예제를 통해 지금까지 배운 개념들이 어떻게 그래픽으로 구현되는지 살펴볼 것이다.
PBR7. 빛의 세기
지금까지 빛의 측정 방법에 대해 배웠습니다. "이런 이론이 실제로 어떻게 쓰이는지" 궁금하셨을 겁니다. 이번 장부터는 이 이론들을 언리얼 엔진에서 어떻게 사용하고 있는지 알아 보도록 하겠습니다.
앞에서 광원의 밝기는 모든 방향으로 나가는 빛의 총량이라고 했습니다. 조도(Illuminance)는 표면에 닿는 빛의 양이었죠. PBR에서는 새로운 조명 개념이 생겼습니다. 바로 면 광원(Area Light)입니다. 면적을 가진 광원을 말합니다. 반대로 점이나 스포트처럼 부피가 없는 조명은 점 광원(Punctual Light)이라고 부릅니다. 실제 생활에서 보는 대부분의 조명은 면 광원입니다.
[그림1. 실제 조명들]
"Punctual"은 "정확한"이라는 뜻입니다. 왜 점 광원을 이렇게 부르는지는 명확하지 않습니다. 일부 프로그램에서는 점 광원을 측정 가능한 광원(Photometric Light)에 포함시키기도 합니다. 광원이 복잡한 형태가 아니라 단순한 점이나 스포트 형태라면 Simple/Isotropic 프로파일이라고 부릅니다.
점 광원은 한 표면에 한 번만 빛이 닿습니다. (전역 조명을 고려하지 않을 때)
Isotropic(등방성)이란?모든 방향에서 똑같다는 뜻입니다. 반대말은 Anisotropic(비등방성)으로, 방향에 따라 달라진다는 의미입니다.[등방성과 비등방성 비교. 출처 : Isotropic and anisotropic minerals.]
(이미지: 등방성과 비등방성 물질의 특징을 비교하는 그림.)
(이미지: 점 광원에서 빛이 사방으로 퍼져나가는 모습과 광선이 한 표면에 한 번만 닿는 것을 보여줌.)
면 광원은 다릅니다. 한 표면에 여러 지점에서 빛이 닿습니다.
(이미지: 면 광원에서 넓게 퍼져나가는 빛이 한 표면에 여러 지점에 닿는 것을 보여줌.)
점 광원과 면 광원은 빛의 세기를 설정하는 방식이 달라야 합니다.
맞습니다. 점 광원은 광도(칸델라, cd)로 설정하고, 면 광원은 광속(루멘, lumen)으로 설정해야 합니다. 점 광원은 특정 방향으로만 빛이 가기 때문에 전체 빛의 양인 광속을 쓰면 안 됩니다.
여러 단위를 사용하는 게 복잡할 수 있습니다. 하지만 점 광원은 "특정 방향으로 얼마나 빛이 가는지"를 표현하기에 광도가 더 편합니다. Frostbite 엔진은 광속, 광도, 조도 중에서 선택할 수 있고, CryEngine은 조도로 설정합니다.
빛의 세기를 광속으로 설정해도 엔진이 알아서 광도나 조도로 바꿔줍니다. 걱정하지 않아도 됩니다.
점광원의 광속으로 광도(candela)를 계산해봅시다. 구 전체의 면적이 이므로, 단위 입체각으로 나가는 빛의 양은 다음과 같습니다.
[식1. 점광원의 광도 계산.]
점광원에 설정한 광속을 라고 하면, 표면에 닿는 조도 는 다음과 같습니다.
[식2. 점광원의 조도 계산.]
앞부분()은 방금 말한 광도 변환입니다. 뒷부분
이 추가된 이유를 설명하겠습니다. r은 광원과 표면 사이의 거리이고, 는 빛 방향과 표면 법선 사이의 각도입니다. 앞에서 조도는 거리와 기울기에 영향을 받는다고 했던 거 기억하시나요?
거리가 멀어지면 빛이 만큼 약해지고, 기울기가 달라지면 만큼 약해집니다. 이런 감쇠를 식에 넣으면 위 식이 완성됩니다.
공식이 나와서 당황스러울 수 있지만, 천천히 생각해보세요. 앞에서 배운 개념들을 공식으로 만든 것뿐입니다.
주의: 아래 그림에서 '한 점'이라고 했는데, 정확히는 '단위 입체각'을 의미합니다.
[그림4. 조도 공식의 구성. 주의 : 그림에서 한 점이라고 했는데, 단위 입체각을 의미합니다.]
(이미지: 광원에서 나오는 빛이 거리()와 각도()에 따라 서피스에 도달하는 조도가 결정되는 과정을 공식과 함께 시각화한 그림.)
6. 언리얼 엔진의 문제점
지금부터는 UE의 문제점에 대해 이야기하겠습니다. 가끔 UE5 구현을 보면 아쉬운 부분이 있습니다. 제대로 확인하지 않고 만든 것처럼 보일 때가 있습니다.
UE5는 광속 단위로 빛의 밝기를 설정합니다. 여기까진 괜찮습니다. 점 광원은 엔진이 알아서 광도로 바꿔주면 되니까요.
문제는 UE5가 로 나누는 걸 빼먹었다는 겁니다. 게다가 거리 제곱 감쇠를 사용할 때 빛의 밝기에 16을 곱합니다.
"16이라는 값은 점 광원이 거리 제곱으로 감쇠될 때 기본 노출에서 적당히 밝게 보이도록 추가한 거야. 1/(4pi) 계산은 안 해."— Brian Karis, Epic Games (출처: UDN)
물리 기반 렌더링인데 제멋대로 값을 설정하고 있습니다. 에너지 보존 법칙에도 맞지 않고, 임의의 값을 곱하기까지 합니다.
"우리는 그 부분에 많은 노력을 들이지 않았어. 명확하게 정리하고 싶은데, 다른 일들을 처리하느라 바빠."— Brian Karis, Epic Games (출처: UDN)
ue5 버전이 나왔는데도 아직 수정되지 않았습니다.
이 문제 때문에 촛불 밝기인 12.57 루멘을 설정해도 실제 촛불처럼 보이지 않습니다. UE5는 100단위가 1m이므로 1257을 입력해야 하지만, 그래도 촛불 같지 않습니다. 감쇠 거리 설정도 명확하지 않습니다.
de45xmedrsdbp.cloudfront.net [언리얼 엔진4 PBR]
7. 언리얼 엔진이 다른 계산 방식을 사용하는 이유
"느낌"과 "직관"의 우선순위:
PBR의 목적: PBR은 물리 공식을 적용하는 것을 넘어, 아티스트가 현실적인 결과물을 직관적으로 얻도록 돕는 것도 중요합니다.
개발자의 언급: "기본 노출에서 합리적인 밝기로 보일 수 있도록 하기 위해 추가한 거야." 이 발언의 의미는 무엇일까요? 아티스트가 물리적인 촛불 값(12.57 루멘)을 입력했을 때, 특정 노출 세팅에서 "이 정도가 실제 촛불 밝기처럼 보이네"라고 직관적으로 납득할 수 있는 시각적 결과를 더 중요하게 여겼다는 뜻입니다. 물리적 정확도가 100%여도 아티스트가 "너무 어두운데?"라고 느끼면 작업하기 어렵습니다.
게임 엔진의 특성: 게임은 실시간 렌더링이 중요하고, 최종적으로 플레이어 눈에 어떻게 보이는지가 가장 중요합니다. 연구나 시뮬레이션 목적의 렌더러와는 우선순위가 다를 수 있습니다.
노출(Exposure) 시스템과의 연계:
카리스가 "기본 노출(exposure)에서"라고 말한 것이 중요합니다. 언리얼 엔진은 실제 카메라처럼 작동하는 자동 노출(Auto Exposure) 시스템을 가지고 있습니다. 이 시스템이 장면 전체의 밝기를 조절하기 때문에, 조명의 절대적인 물리 값이 특정 노출에서 어떻게 보이는지는 별개의 문제입니다.
16이라는 보정 값은 특정 노출 시스템 설정과 맞물려 아티스트가 선호하는 밝기 범위를 유지합니다. 16을 제거하면 아티스트는 조명 값을 로 곱하는 것 외에도 노출 세팅을 추가로 조절해야 하는 번거로움이 생깁니다.
하위 호환성 및 기존 콘텐츠 보호:
엔진의 핵심 코드를 변경하는 것은 매우 신중해야 합니다. 나누기와 16 곱하기를 제거하면, 언리얼 엔진으로 만들어진 수많은 프로젝트의 모든 조명이 갑자기 이상하게 보이게 됩니다. 이는 엄청난 재작업을 유발하며 개발사들에게 큰 부담을 줍니다.
엔진 업데이트 시 기존 프로젝트와의 호환성을 유지하는 것은 매우 중요합니다. "할 일 목록에 다른 것들이 많아 바쁘다"는 발언은 이러한 기술 부채(Technical Debt)와 대규모 변경의 위험 부담 때문에 우선순위가 밀려 있다는 의미로 해석됩니다.
복잡한 조명 시스템에서의 단순화:
모든 조명 유형(Punctual, Area, Sky Light 등)에서 100% 완벽한 물리적 정확성을 일관되게 유지하는 것은 매우 복잡합니다. 특히 Area Light의 경우 더욱 그렇습니다. 어떤 지점에서는 완벽하지 않더라도 "충분히 좋은" 시각적 결과와 "아티스트가 이해하기 쉬운" 인터페이스를 제공하는 것이 더 효율적인 해결책이라고 판단했을 수 있습니다.
이해도와 학습 곡선:
물리 기반 렌더링의 세부적인 수학적, 물리적 개념은 비전문가 아티스트에게 어려울 수 있습니다. 엔진은 이런 복잡성을 숨기고 아티스트가 '루멘' 같은 직관적인 단위로 작업할 수 있도록 돕습니다. 일부 내부적인 '꼼수'가 있더라도, 아티스트가 원하는 결과를 쉽고 빠르게 얻을 수 있다면 그 '꼼수'는 실용적인 가치를 가질 수 있습니다.
8. 정리
현재 UE4는 조도 계산에서 로 나누지 않고 16을 곱하는 등 물리적으로 정확하지 않습니다. 그래서 외부 자료의 값을 바로 사용하기 어렵고, 감쇠 거리 설정도 불명확합니다. 게다가 조명 종류마다 세기 설정 방식이 달라 일관성이 없습니다.
PBR을 사용할 때 중요한 것은 "단순하고 일관되게" 만드는 것입니다. 아티스트가 값을 정할 때 헷갈리지 않아야 합니다. 외부 자료를 참고해서 쉽게 자신만의 설정값을 만들 수 있어야 합니다.
그러니 엔진 코드를 제대로 고치거나, 문제를 알고 적절히 계산해서 값을 입력해야 합니다. 또는 감쇠 거리로 루멘을 계산해주는 도구를 만드는 것도 좋은 방법입니다.
지금까지 빛과 계산 방법의 기본 개념을 설명했습니다. 지루하셨을 수도 있지만, 이 용어들은 앞으로 계속 나올 것이므로 읽은 시간이 아깝지 않을 겁니다.
다음 시간부터는 본격적으로 PBR을 다루겠습니다. 실제 예제를 중심으로 렌더링 결과를 비교하면서 진행할 예정입니다.
PBR 8: 감쇠 반경 (Attenuation Radius)
1. 거리 감쇠 (Distance Attenuation)
[3. 빛의 감쇠]에서 빛의 감쇠는 물리적으로 (거리 제곱의 역수) 공식을 따른다고 했습니다. 하지만 컴퓨터 프로그램에서는 이 공식을 그대로 사용할 수 없습니다.
•
문제점 1 (Division by Zero): 거리가 0인 지점(dist = 0)에서 이 되어 값이 무한대(Infinity)가 됩니다.
•
문제점 2 (Energy Conservation): 광원과 거의 0에 가까울 때 빛이 원래 밝기보다 더 밝아지는 것은 에너지 보존 법칙에 위배됩니다.
이 문제들을 해결하기 위해 UE4는 식1과 같이 수정된 감쇠 공식을 사용합니다.
식1. UE4의 거리 감쇠 공식
(여기서 DistanceBias는 쉐이더 코드에서 1로 고정되어 있습니다.)
[그림1. 과 의 비교]
(이미지: 파란색 그래프(수정된 공식)가 일 때 1에서 시작하여 점차 감쇠하는 모습과, 빨간색 그래프(원본 공식)가 0에서 무한대로 치솟는 모습 비교)
[그림1]에서 볼 수 있듯이, 수정된 공식(파란색 그래프)은 거리가 0일 때 최대값을 1로 제한하여 앞서 언급한 두 문제를 해결합니다.
하지만 이 공식에도 실용적인 문제가 남아있습니다. [그림1]의 파란색 그래프는 거리가 아무리 멀어져도 0에 수렴할 뿐, 절대로 0이 되지 않습니다. 즉, 이 빛은 세기가 약해질 뿐 무한대의 거리까지 영향을 미칩니다.
2. 감쇠 반경 마스크 (Attenuation Radius Mask)
실제 씬에는 수백, 수천 개의 광원이 존재할 수 있습니다. 만약 모든 광원이 씬의 모든 픽셀에 (아무리 약하더라도) 영향을 미친다고 계산하면, 그 비용은 감당할 수 없을 정도로 비쌉니다.
[그림3]에서 보듯, 특정 거리 이상 멀어지면 빛은 시각적으로 거의 영향을 미치지 못합니다.
[그림3. 감쇠 시각화]
(이미지: 광원에서 멀어질수록 빛이 약해져 거의 보이지 않게 되는 모습)
이러한 이유로, 대부분의 엔진은 광원이 영향을 미치는 거리를 강제로 제한하는 속성을 가지고 있습니다. 이것이 바로 **"감쇠 반경 (Attenuation Radius)"**입니다. (UE4는 내부적으로 "Light Radius Mask"라고 부릅니다.)
이 마스크는 식2와 같이 복잡한 함수로 계산됩니다.
식2. LightRadiusMask 공식
(여기서 saturate() 함수는 값을 0과 1 사이로 강제 변환합니다.)
이 식을 완전히 이해할 필요는 없습니다. 중요한 것은 이 함수의 효과입니다. [그림4]는 이 공식을 그래프로 나타낸 것입니다.
[그림4. LightRadiusMask 그래프]
(이미지: Radius가 1일 때 Dist가 1이 되면 값이 0이 되고, Radius가 2일 때 Dist가 2가 되면 값이 0이 되는 그래프)
[그림4]에서 보듯이, 이 마스크는 거리가 아티스트가 설정한 Radius 값에 가까워질수록 부드럽게 0으로 수렴하여, Radius를 넘어가면 빛의 세기를 완전히 0으로 '잘라버리는' 역할을 합니다.
3. 거리 감쇠와 감쇠 반경의 결합
최종적으로 광원에서 사용되는 감쇠 공식은 앞서 설명한 두 식(식1, 식2)을 곱한 것입니다.
식3. 최종 감쇠 공식
[그림5]는 빛의 밝기가 10일 때, Radius 값에 따라 이 최종 감쇠 공식이 어떻게 변하는지 보여줍니다.
[그림5. 빛 밝기 10일 때 최종 감쇠 그래프]
(이미지: Radius가 클수록(예: 10) 그래프가 자연스러운 곡선을 따르다 잘리고, Radius가 작을수록(예: 2, 4) 곡선이 부자연스럽게 일찍 꺾이는 모습)
[그림5]에서 주목할 점은 Radius 값이 클수록 최종 그래프가 원래의 자연스러운 감쇠 곡선과 유사해진다는 것입니다. 반대로 Radius를 지나치게 작게 설정하면 빛이 충분히 감쇠되기 전에 마스크의 영향을 받아 본래의 곡선과는 전혀 다른 부자연스러운 형태로 감쇠됩니다.
PBR9. Global Illumination
1. 빛의 복잡한 경로
지금까지는 빛이 표면에서 한 번 반사되어 눈에 들어오는 단순한 경우를 다뤘습니다. 하지만 실제 세계에서는 [그림1]처럼 빛이 산란(Scattering), 투과(Transmission), 반사(Reflection), 흡수(Absorption) 등 훨씬 복잡한 경로를 거쳐 우리 눈에 도달합니다.
[그림1. 다양한 경로로 눈에 들어오는 빛]
2. Local Illumination (지역 조명)
컴퓨터 성능의 한계로 실시간 그래픽스에서 이 모든 경로를 계산하는 것은 불가능합니다. 그래서 PBR 이전의 전통적인 방식(Local Illumination)에서는 빛이 직접 닿는 부분만 계산했습니다.
•
문제점: 이 방식은 빛이 직접 닿지 않는 그림자 영역을 완전한 검은색으로 만들어 부자연스러운 결과를 냅니다.
•
해결책 (비물리적): 이를 해결하기 위해 '주변광(Ambient Light)'이라는 가상의 빛을 추가하여 어두운 부분을 아티스트의 감각에 의존해 인위적으로 밝혔습니다.
3. Global Illumination (GI / 전역 조명)
Local Illumination의 한계는 명확합니다. 실제 세계에서는 표면에 닿은 빛이 반사되거나 굴절되어 그 자체가 새로운 광원처럼 작동하기 때문입니다.
•
정의: 물체 표면에서 반사, 굴절되는 모든 빛을 새로운 광원으로 삼아 계산하는 방식을 **Global Illumination (GI)**이라고 부릅니다.
•
결과: 그림처럼 굴절과 반사가 제대로 적용되어 실세계에서 보는 것처럼 훨씬 자연스럽고 복잡한 결과가 나옵니다.
GI의 핵심 구성 요소
GI는 크게 두 가지 빛으로 나뉩니다.
1.
Direct Light (직접광): 광원에서 나와 표면으로 직접 들어온 빛.
2.
Indirect Light (간접광): 다른 표면에 반사되어 새로운 광원처럼 들어온 빛.
[그림5]는 직접광(Direct light)만 계산한 결과입니다. 여기에 바닥에 반사된 빛(1-bounced indirect light)이 추가되면 어두웠던 부분이 밝아집니다. 이 빛이 다시 반사되면(2-bounced) 더 자연스러워집니다.
•
Bounce(반사 횟수)가 많을수록 더 자연스럽지만 계산 비용이 기하급수적으로 증가합니다.
•
LPV, SVOGI, IBL 등은 이 비싼 계산을 실시간으로 근사(approximate)하기 위한 기술들입니다.
언리얼의 GL을 자세히 보고싶다면 다음 공식 Document에 접근해보면 됩니다.
PBR10. Image Based Lighting
[Global Illumination & Indirect Lighting] 문서에서 GI를 위해 간접광(Indirect Light)이 필수적이라고 설명했습니다.
광원이 있으면 그 광원으로부터 간접광을 계산할 수 있습니다. 하지만 씬의 모든 광원을 일일이 배치하고 계산하는 것은 현실적으로 어렵습니다. 그래서 그래픽스 연구자들은 간접광을 이미지로부터 얻는 방법을 고안했고, 이것이 오늘날 널리 사용되는 Image Based Lighting (IBL)입니다.
이 문서에서는 IBL 기법이 어떻게 발전했고, 어떤 개념으로 이루어져 있는지 다룹니다.
1. Cubemap (큐브맵)
그래픽스 카드는 큐브맵(Cubemap)이라는 특수 텍스처를 지원합니다. 큐브맵은 한 시점을 중심으로 주변 환경을 6면의 텍스처(정육면체 형태)에 미리 렌더링하여 저장하는 방식입니다. 보통 특정 위치에서 여러 방향으로 사진을 찍고 이를 보정하여 합쳐서 만듭니다.
큐브맵이 실시간 그래픽스에서 처음 사용된 곳은 스카이박스(SkyBox)와 스카이 스피어(SkySphere)였습니다.
[그림1. 스카이 큐브맵]
(이미지: 정육면체의 6면에 하늘과 풍경이 펼쳐진 큐브맵 텍스처)
[그림2. 스카이 큐브맵 렌더링 결과]
(이미지: 큐브맵으로 렌더링된 하늘과 지평선 풍경)
큐브맵은 주로 원경(먼 배경)에 사용되었기 때문에 거리에 의한 왜곡 영향이 적었고, 시각적 품질도 괜찮았습니다.
2. Environment Mapping (환경 매핑)
큐브맵을 이용해 금속의 반사를 표현하려는 시도가 있었습니다. 1976년 Blinn과 Newell의 논문을 시작으로 80~90년대 초반에 여러 연구자들에 의해 발전했습니다.
이러한 기법을 환경 매핑(Environment Mapping) 또는 반사 매핑(Reflection Mapping)이라고 부릅니다. 그래픽스 하드웨어가 큐브맵을 지원하면서 쉽게 구현할 수 있게 되었습니다.
[그림3. 환경 매핑 예제]
(이미지: 주전자 표면에 큐브맵의 환경이 반사되어 비치는 모습)
큐브맵의 좌표는 [그림4]처럼 큐브(정육면체)의 중심을 원점으로 하는 좌표계로 표현됩니다.
[그림4. 큐브맵 좌표계]
[그림5]에서처럼 표면의 법선(Normal)과 카메라를 향하는 벡터(View Vector)를 알면 반사 벡터(Reflection Vector)를 쉽게 계산할 수 있습니다. 이 반사 벡터 방향에 있는 큐브맵의 색상을 가져와 물체 표면에 칠하는 방식입니다.
[그림5. 환경 매핑 좌표 구하기]
또한 구가 큐브 대신에 매핑에 사용 될 수 있음을 보여줍니다. 벡터는 길이가 달라도 방향이 동일하면 정규화(normalize)했을 때 같은 벡터가 되며, 이를 큐브맵의 좌표로 사용합니다.
환경 매핑은 주로 금속의 반사 효과를 표현하는 데 사용되었습니다.
3. Image Based Lighting (IBL)
하드웨어 성능이 발전하면서 환경 매핑을 한 단계 더 발전시켜 광원으로 사용하려는 시도가 이루어졌습니다. 이것이 바로 Image-Based Lighting (IBL) 개념입니다. Paul Debevec 등의 연구자들이 이 분야를 주도했습니다.
IBL과 환경 매핑의 가장 큰 차이는 이미지를 광원으로 사용하는지 여부입니다.
4. IBL Diffuse (난반사)
표면에 들어온 빛은 [그림7]처럼 반사(reflected), 투과(transmitted), 흡수(absorbed)됩니다.
[그림7. 빛의 반사, 투과, 흡수]
반사 성분은 [그림8]처럼 난반사(Diffuse Reflection)와 정반사(Specular Reflection)로 크게 나뉩니다.
[그림8. 난반사와 정반사]
기존 환경 매핑은 큐브맵을 정반사(Specular) 성분으로만 사용했습니다(주로 금속 표현). 하지만 이미지를 제대로 된 광원으로 사용하려면 난반사(Diffuse) 성분도 고려해야 합니다.
GI 관점에서 보면, [그림9]처럼 주변 환경에서 오는 빛이 표면에 도달하는 조도(illuminance, irradiance) 역할을 해야 합니다. 이러한 정보를 담고 있는 것을 Irradiance Map (조도 맵)이라고 부릅니다.
[그림9. IBL에서의 Irradiance 계산]
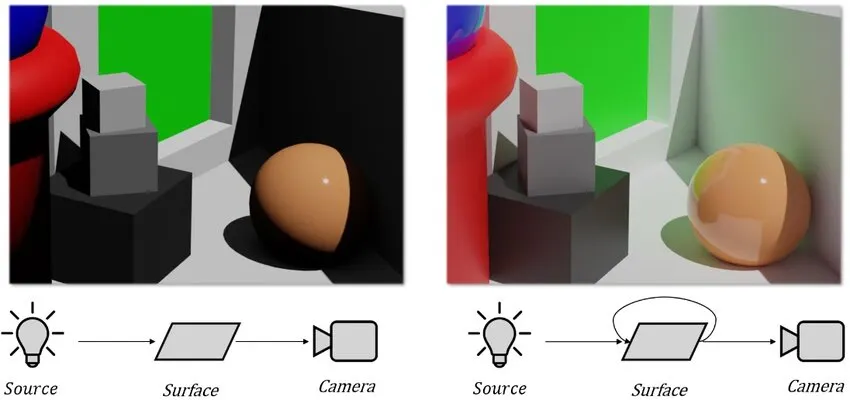
왼쪽 시나리오는 카메라에서 바라보는 시점 방향을 미러링하기 위해 법선을 사용하는 반사 큐브맵을 나타냅니다 . 반면, 디퓨즈 큐브맵은 환경 맵을 투영한 것일 뿐이므로 시점 방향의 영향을 받지 않습니다. 따라서 다음 영상과 같이 카메라 시점의 영향을 받지 않습니다.
Irradiance Map은 난반사 성분을 담고 있기 때문에 원본 이미지보다 [그림10]의 오른쪽 큐브맵처럼 뭉개지고 흐릿한 느낌이 납니다.
[그림10. Irradiance Map 샘플]
여기서 한 가지 문제가 발생합니다. 큐브맵 텍스처를 샘플링하는 것은 비용이 비싼 작업입니다. 특히 [그림9]처럼 난반사를 계산하려면 매우 넓은 영역을 수만 번 샘플링해야 합니다(128x128 큐브맵의 diffuse 계산에 50,000번 샘플링 필요).
그래서 연구자들은 더 단순하게 계산하는 방법을 찾았는데, 그것이 바로 Spherical Harmonics (SH, 구면 조화)입니다.
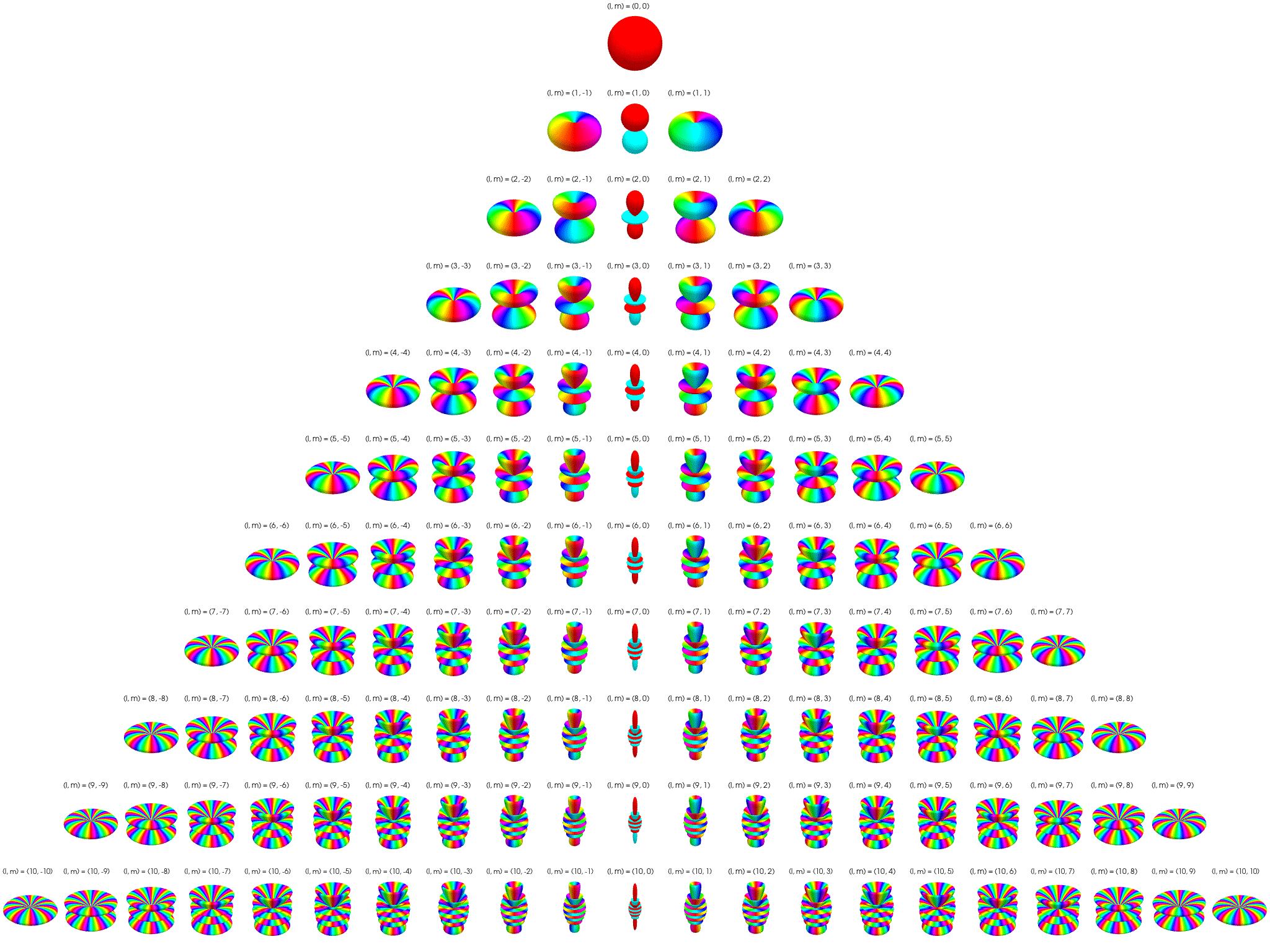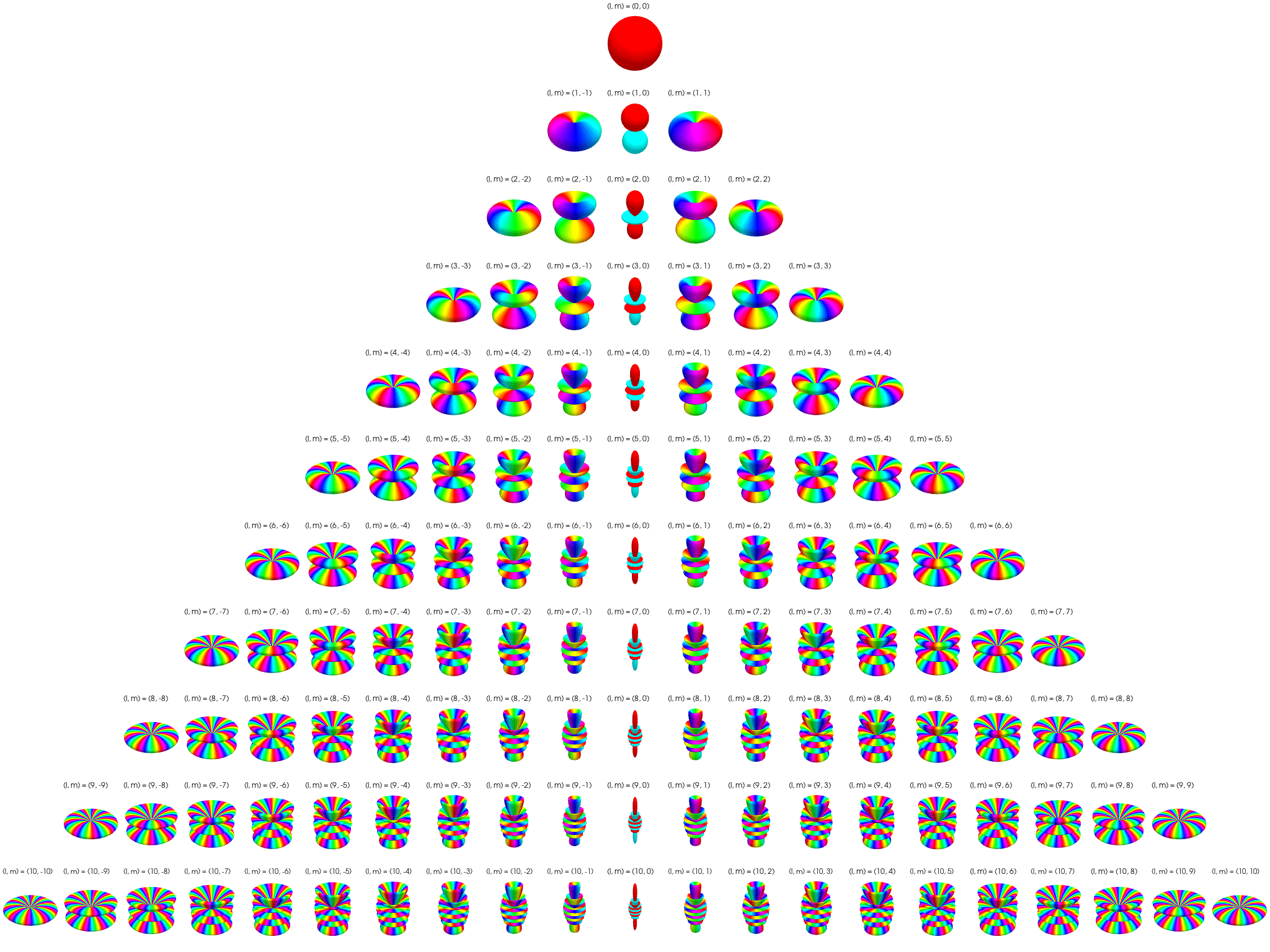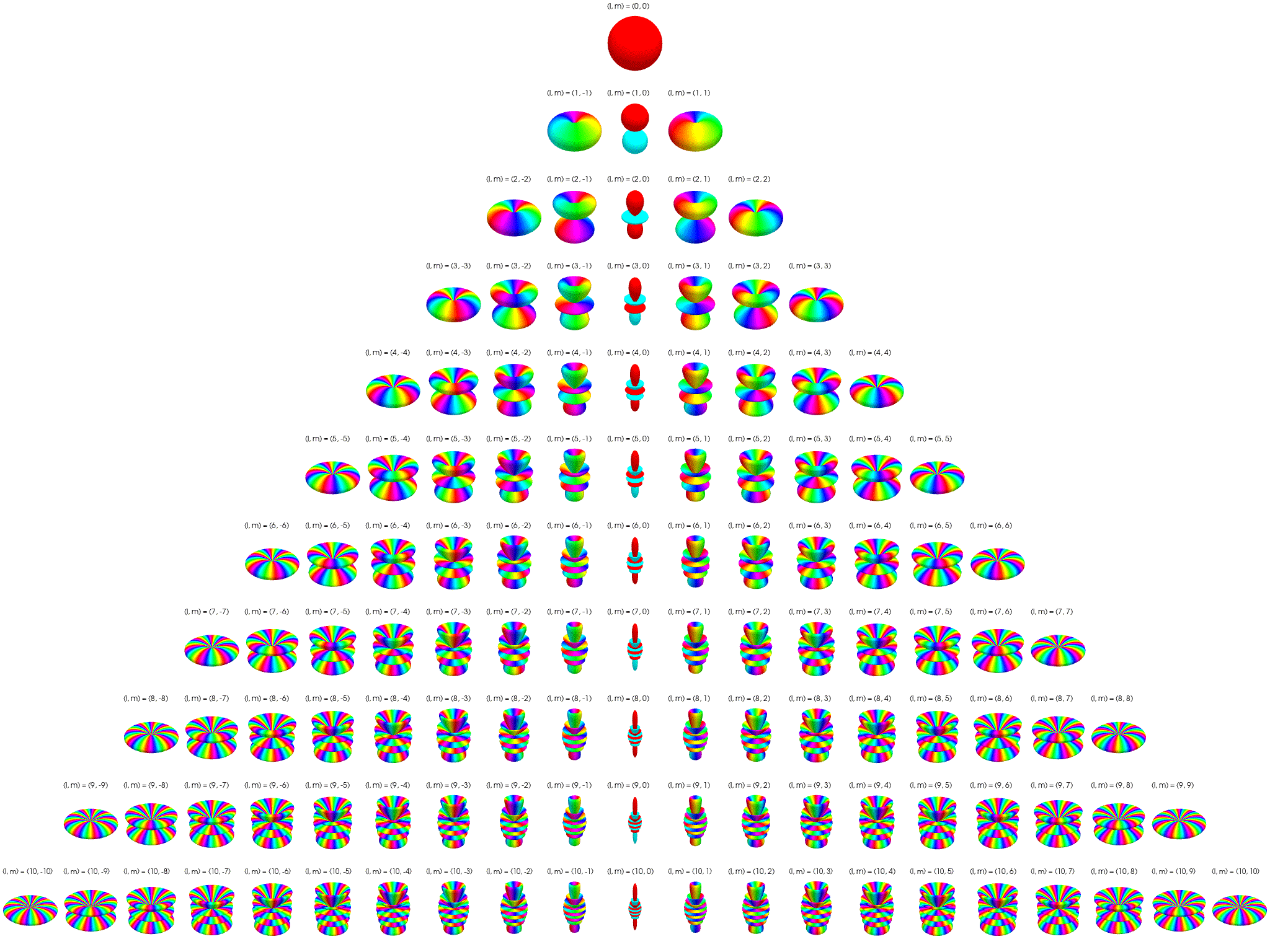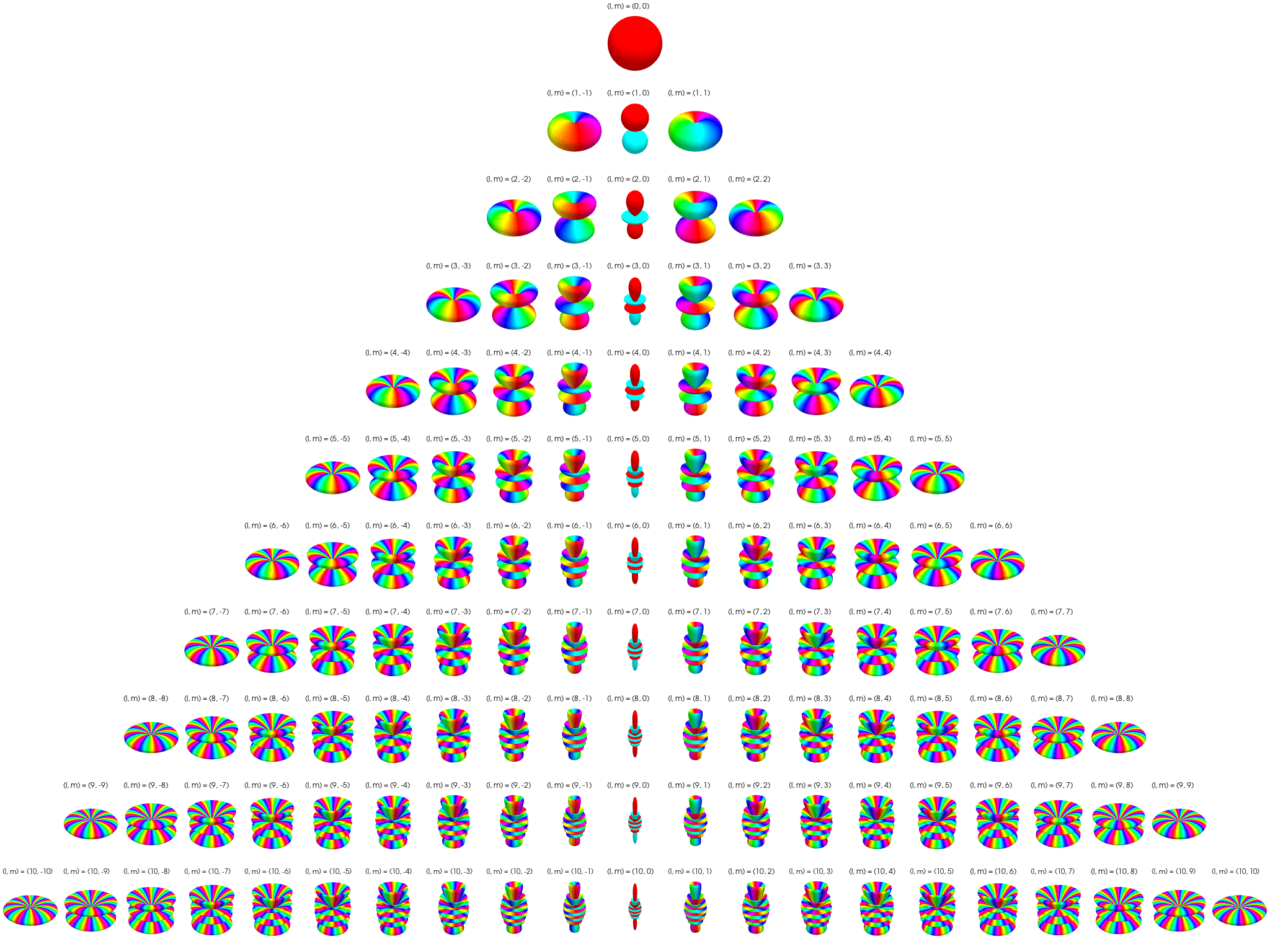
SH는 [그림11]처럼 구형 표면의 형태를 수학적으로 표현하는 방식입니다. 계수(l)가 클수록 더 디테일한 모양을 표현할 수 있습니다.
[그림11. Spherical Harmonics 예제]
이 SH를 사용하여 [그림10]의 Irradiance Map 정보를 [그림12]처럼 구형 표면에 매핑한 후 단순한 함수로 압축합니다. 이렇게 각 텍셀을 SH 함수로 만들면 빛이 나가는 경향과 세기가 결정됩니다.
우리가 사용하는 Irradiance Map은 단순히 diffuse 정보를 저장한 것이 아니라 SH 계수들을 저장한 것이라고 이해하면 됩니다.
[그림12. Irradiance Map을 구에 매핑했을 때의 느낌]
IBL Diffuse를 적용하면 [그림13]과 같은 결과가 나옵니다.
[그림13. IBL Indirect Diffuse 결과]
5. IBL Specular (정반사)
정반사(Specular) 성분은 환경 매핑에서 다룬 것과 큰 차이는 없지만, PBR에서는 Roughness(거칠기)라는 개념이 도입됩니다. [그림14]처럼 표면의 거칠기 정도에 따라 반사의 선명도가 달라집니다.
[그림14. Roughness에 따른 매끈함의 변화]
일반적으로 거칠기에 따른 반사의 흐릿함(blurring)을 표현하기 위해 [그림15]처럼 밉맵(mipmap)을 만들어 사용합니다. LOD(Level of Detail) 레벨이 높아질수록 Roughness가 높은 것으로 간주하여 흐릿한 밉맵을 가져옵니다.
[그림15. 반사맵 밉맵]
[그림16. Roughness 0.1에서의 IBL Indirect Specular 예시]
6. 정리
IBL은 이미지를 광원으로 취급하여 간접광 성분을 얻는 방식입니다. 실시간 GI 구현이 어려운 상황에서 유용한 대안이며, 실시간 GI와 함께 사용되는 경우도 많습니다.
실제 엔진에서는 Diffuse뿐만 아니라 Specular 역시 중요도 샘플링(Importance Sampling) 같은 복잡한 방식을 사용하여 정확한 결과를 얻습니다. 이 기법은 반사, Area Light, Ray-tracing, 적분 등의 주제와 관련이 있어 여기에서 자세히 다루기에는 내용이 무겁습니다. (자세한 내용은 "IBL Importance Sampling" 등의 키워드로 검색해 보세요.)
UE의 경우 Split Sum Approximation과 Prefiltered Environment Map이라는 기법을 사용하여 IBL Specular를 구현합니다.
PBR11. 모든 것은 빛납니다 (Everything is Shiny)
지금까지는 조도(Illuminance)를 다뤘다면, 이번 문서부터는 휘도(Luminance)를 중점적으로 다룹니다.
PBR(물리 기반 렌더링) 라이팅 모델에서 휘도를 계산하는 방식은 기존 라이팅 모델과 여러 면에서 다릅니다. 특히 아티스트 입장에서는 디퓨즈(Diffuse)와 스페큘러(Specular)가 계산되는 방식에서 가장 큰 차이를 느낄 것입니다.
과거에는 아티스트가 디퓨즈와 스페큘러의 세기를 직접 설정해야 했습니다. 완벽한 이해보다는 '감'에 의존해 값을 조절하는 방식이었습니다.
하지만 PBR에서는 Metalicity(금속성)와 Roughness(거칠기)라는 물리 기반 파라미터로 디퓨즈와 스페큘러 성분을 조절합니다. 처음에는 낯설 수 있지만, 이 값들은 명확한 물리적 의미를 가지므로 다음과 같은 장점이 있습니다.
•
통일성 증대: 모든 재질에 물리적으로 일관된 빛 반응을 적용할 수 있습니다.
•
생산성 증가: 라이팅 종류나 오브젝트별로 값을 일일이 조정할 필요가 줄어듭니다.
따라서 PBR이 휘도를 계산하는 배경 개념을 이해하는 것은 올바른 재질 설정을 위해 중요합니다. PBR을 처음 접하는 아티스트들이 "디퓨즈 맵에 그린 대로 결과가 나오지 않는다"고 말하는 경우가 많은데, 이는 디퓨즈와 스페큘러가 어떻게 반영되는지 이해하지 못해서 생기는 당연한 질문입니다.
휘도를 다루는 데 있어 빛의 반사 성질과 구성 요소를 이해하는 것은 매우 중요합니다. 에너지 보존 법칙, Metalicity, Roughness 같은 개념을 처음부터 설명하는 것은 어려울 수 있습니다.
가끔 초심자용 온라인 문서나 논문에서 스페큘러(Specular)에 대한 언급을 보게 됩니다. 그중 "옷이나 판지(cardboard)와 같은 일부 재질은 스페큘러를 가지지 않는 순수한 디퓨즈 표면입니다"라는 문장을 접하곤 합니다. 이는 거짓입니다.
실세계에 존재하는 모든 물체는 스페큘러를 가집니다. 심지어 매우 오래된 옷이나 판지도 스페큘러를 가집니다. 필자는 집에서 만든 편광(polarization) 설정으로 이를 확인했습니다. 편광 필터를 수작업으로 만들었기 때문에 여기서 보여주는 구분이 완벽하지는 않지만, 충분히 잘 작동합니다.
먼저 면직물 셔츠부터 살펴보겠습니다. 이것은 필자가 구할 수 있는 가장 디퓨즈(diffuse)한 재질 중 하나입니다. 대부분의 면직물 셔츠는 이보다 더 많은 스페큘러를 가집니다.
면직물 셔츠
Main
Diffuse
Specular
데님
Main
Diffuse
Specular
맙소사! 판지도 빛납니다.
Main
Diffuse
Specular
벽돌
Main
Diffuse
Specular
접시
Main
Diffuse
Specular
보도의 콘크리트는 포장도로보다는 덜 빛납니다.
Main
Diffuse
Specular
PBR 12. 모든 것은 프레넬을 가집니다 (Everything has Fresnel)
게임에서 표준 스페큘러(Specular) 라이팅 모델이 자주 사용되지만, 게임에서 거의 보기 힘든 효과 중 하나가 바로 프레넬(Fresnel)입니다.
1. Blinn-Phong 스페큘러 모델의 한계
비디오 게임에서 가장 일반적인 스페큘러 모델은 Blinn-Phong이며, 다음과 같이 정의됩니다:
H = normalize( V + L )
specVal = pow( saturate( dot( H, N ) ), power );
JavaScript
복사
여기서 V는 뷰 벡터, L은 라이트 벡터, N은 노멀 벡터이며, power는 스페큘러의 날카로움을 조절합니다. H는 뷰 벡터와 라이트 벡터의 중간을 가리키는 하프 벡터입니다.
이 모델은 어떻게 작동할까요? 다음 다이어그램을 봅시다.
[이미지: 뷰, 라이트, 노멀 벡터가 그려진 다이어그램. 하프 벡터(H)가 노멀(N)과 일치할 때 스페큘러 최대값 발생.]
스페큘러 하이라이트가 가장 밝게 나타나는 곳은 어디일까요? 직관적으로, 뷰 벡터가 라이트 벡터의 반사 벡터와 일치할 때 스페큘러가 최대가 됩니다. 이는 하프 벡터 H가 노멀 N에 정확히 정렬될 때 발생합니다.
이제 다른 경우를 봅시다.
[이미지: 위와 유사하지만, 물체를 보는 각도가 달라진 다이어그램. 뷰 벡터가 라이트 벡터로 반사됨.]
이 경우에도 뷰 벡터는 라이트 벡터로 반사됩니다. 스페큘러 하이라이트가 첫 번째 경우보다 더 밝을까요, 더 흐릿할까요, 아니면 같을까요? Blinn-Phong 모델의 계산 결과는 같습니다. 두 경우 모두 스페큘러 하이라이트의 최댓값을 보고 있기 때문입니다. 하지만 실세계에서도 동일할까요? 아니요.
2. 벽돌 예제를 통한 Blinn-Phong의 문제점
다음은 서로 다른 각도에서 촬영한 벽돌 사진입니다.
•
빛과 카메라가 모두 아래를 향합니다. 비교적 정면에서 보는 각도입니다.
•
빛이 지표각(grazing angle, 비스듬한 각도)에서 비춥니다.
편광 필터로 스페큘러와 디퓨즈를 분리했습니다. 왼쪽은 디퓨즈, 오른쪽은 스페큘러입니다.
Blinn-Phong 모델에 따르면 두 경우의 스페큘러는 동일한 세기를 가져야 합니다. 하지만 현실에서는 지표각에 가까울수록 스페큘러가 훨씬 더 밝아집니다. 벽돌처럼 단순한 재질에서도 Blinn-Phong 모델은 실제와 다른 결과를 냅니다. 이 현상이 바로 프레넬(Fresnel)입니다.
3. 프레넬 효과 (Fresnel Effect)
[이미지: 위와 동일한 다이어그램 두 개가 나란히 배치됨. 뷰 각도가 달라질 때 스페큘러 밝기가 어떻게 변해야 하는지 암시.]
이 효과를 다루기 위해 프레넬을 사용할 수 있습니다. 프레넬을 실시간으로 근사 계산하는 좋은 방법 중 하나는 Schlick Fresnel입니다. GPU Gem 3의 피부 챕터에서 이 공식을 찾을 수 있습니다:
float base = 1 - dot( V, H );
float exponential = pow( base, 5.0 );
float fresnel = exponential + F0 * ( 1.0 - exponential );
specVal *= fresnel;
JavaScript
복사
여기서 F0은 표면을 정면에서 봤을 때 반사하는 빛의 양을 나타내는 기본 반사율입니다. 이 fresnel 값을 기존 스페큘러 값(specVal)에 곱하면 프레넬 효과가 적용됩니다.
4. 모든 재질에 존재하는 프레넬
대부분의 사람들은 물, 유리, 금속처럼 매우 밝게 빛나는 표면에서만 프레넬 효과가 나타난다고 생각합니다. 하지만 실제로 프레넬은 거의 모든 재질에 존재하는 강한 효과입니다.
필자는 프레넬이 덜 빛나는 재질에서 시각적으로 더 중요한 역할을 한다고 주장합니다. 아무것도 없던 곳에서 강한 스페큘러가 나타나는 것이, 이미 높은 스페큘러를 더 높이는 것보다 시각적으로 더 중요하기 때문입니다.
다음은 PVC 파이프의 일부입니다.
[이미지: PVC 파이프 사진. Main, Diffuse, Specular.]
PVC는 분명히 프레넬을 가집니다. 필자의 관점에서는 PVC보다 벽돌에서 프레넬이 시각적으로 더 중요합니다. 물, 유리, 금속만을 위해 프레넬을 고려하는 것은 잘못된 접근입니다. 프레넬은 덜 빛나는 표면에서 더 큰 시각적 차이를 만들기 때문입니다.
몇 가지 예제가 더 있습니다.
•
싸구려 판지: 흔히 "순수 디퓨즈 재질"로 오해받지만, 실제로는 지표각에서 매우 밝은 스페큘러 반사를 보여줍니다. 직각에서는 미묘한 채도 감소를 더합니다.
•
포장도로: 아침에 운전할 때 포장도로가 더 밝게 보이는 이유가 태양이 눈에 들어오기 때문이라고 생각할 수 있습니다. 하지만 주요 원인은 포장도로가 매우 강한 프레넬을 가지고 있기 때문입니다. 다음에 운전할 때 사이드 미러를 확인해보세요. 미러에 보이는 포장도로가 전면에 있는 포장도로보다 얼마나 어두운지 알 수 있을 것입니다.
•
수건: 거친 면 재질은 일반적인 재질보다 스페큘러가 적습니다. 두 번째 이미지가 전체적으로 더 밝아서 스페큘러와 디퓨즈의 상대적 변화를 보기 어렵습니다.
•
X-Rite 컬러 체커: 컬러 체커를 사용할 때 카메라로부터 수직으로 배치하는 것이 좋습니다. 이제 그 이유를 아실 것입니다. (프레넬 효과를 최소화하기 위함)
18. Distribution Function (분포 함수)
그래픽스에 익숙한 분들이라면 BSDF, BRDF, BTDF와 같은 용어를 접해봤을 겁니다. 모두 DF라는 공통 접미사를 가지는데, 이는 Distribution Function(분포 함수)의 약자입니다.
3D 저작 도구에서 BRDF라는 용어를 흔히 볼 수 있습니다.
명시적으로 BRDF라는 용어를 사용하지 않더라도, "Glossiness"나 "Specular Power" 같은 BRDF 관련 파라미터를 사용하는 경우가 많습니다. 이것들은 주로 Phong이나 Blinn-Phong 쉐이딩 모델을 위한 BRDF 파라미터입니다.
BRDF를 자세히 알지 못하더라도, [그림5]처럼 다양한 쉐이딩 모델을 비교하는 글을 본 적이 있을 겁니다.
[그림5. BRDF 비교]
이러한 쉐이딩 모델의 차이는 어디에서 발생할까요? 바로 분포 함수(Distribution Function)의 차이입니다.
1. 함수(Function)란?
함수란 입력(x)이 들어오면 특정 출력(f(x))을 내보내는 기계 상자와 같습니다.
[그림6. 함수를 기계에 비유함]
수학에서 함수는 반드시 입력(x)과 출력(f(x))이 1:1로 대응해야 합니다. 하나의 입력에 여러 출력이 나올 수 있다면, 그 기계는 신뢰할 수 없기 때문입니다.
•
정의역: x가 될 수 있는 값들의 집합
•
치역: f(x)의 값이 될 수 있는 값들의 집합
•
공역: f(x) 값들이 모여 있는 전체 공간 (치역은 공역의 부분집합)
중요한 점은, 어떤 식의 입력값과 출력값이 반드시 1:1로 대응해야만 그 식을 함수라고 부를 수 있다는 것입니다.
2. 분포(Distribution)란?
"분포"는 확률이나 통계에서 자주 등장하는 개념으로, 어떤 요소들이 일정한 범위에 퍼져 있는 모양, 즉 특정 패턴을 의미합니다. 이를 함수로 나타낸 것이 분포 함수입니다.
[그림9. 정규분포 그래프], [그림10. 주사위 두 개를 던질 때의 확률 분포]
그래픽스에서의 분포는 해석학 영역에 속해 조금 다른 의미를 가지기도 하지만, 여기서는 단순히 "분포는 패턴"이라고 이해하는 것이 좋습니다.
그래픽스에서 분포는 [그림11]처럼 로브(lobe) 형태로 표현되는 경우가 많습니다. '로브'는 어떤 물체의 둥글거나 평평한 부분을 뜻합니다. 쉐이더 비교 글에서 이런 그림을 본 적이 있을 것입니다.
[그림11. 여러 반사 로브 표현]
이러한 로브는 빛의 세기를 나타냅니다. [그림12]에서 붉은색 A, B, C는 관찰자의 위치입니다. 녹색 "Standard Phong specular lobe"를 예로 들어봅시다.
[그림12. Lobe와 관찰자 A, B, C의 관계]
•
원점 O에서 OA, OB, OC가 녹색 로브와 만날 때까지의 길이가 스페큘러의 세기를 의미합니다.
•
OB는 OA보다 로브와 만나는 길이가 길므로, 관찰자가 B에 있을 때 A에 있을 때보다 스페큘러를 더 강하게 받습니다.
•
OC는 로브와 만나지 않으므로 스페큘러 세기는 0입니다.
로브의 모양만 봐도 스페큘러가 뾰족하게 보일지, 아니면 넓게 퍼져 보일지를 알 수 있습니다.
PBR의 선구자인 Disney는 BRDF를 연구하기 위해 BRDF Explorer라는 툴을 만들었습니다.
[그림13]처럼 2D와 3D에서 로브를 확인하고 BRDF 모델을 직접 만들어 볼 수 있습니다. 쉐이더 개발 전 아티스트와 결과를 미리 확인하는 데 유용합니다.
[그림13. Disney BRDF Explorer 스크린샷]
3. BRDF와 BTDF
[휘도 측정] 문서에서 BRDF, BTDF 그림을 보여준 적이 있습니다.
[그림14. BRDF와 BTDF]
•
BRDF (Reflectance Distribution Function, 반사율 분포 함수): 표면에서 반사되어 나가는 빛의 분포를 다룹니다.
•
BTDF (Transmittance Distribution Function, 투과율 분포 함수): 표면을 투과하여 나가는 빛의 분포를 다룹니다.
쉽게 말해, 표면에 들어온 빛이 얼마만큼 반사되고 얼마만큼 투과되는지를 함수로 나타낸 것입니다. 반사는 다시 Diffuse RDF와 Specular RDF로 나뉩니다.
우리가 자주 접하는 분포 함수 앞에는 "B"가 붙어 "Bidirectional(쌍방향)"을 의미합니다. 이는 [그림15]처럼 빛과 관찰자의 위치가 바뀌어도 관계만 같으면 결과(반사율 또는 투과율)가 동일하다는 뜻입니다. 반사의 경우, 입사각과 반사각의 관계가 동일하면 어디에 있든 항상 같은 결과가 나온다는 의미입니다.
[그림15. Bidirectional의 의미]
왜 Bidirectional이 필요한가?
컴퓨터 그래픽스, 특히 실시간 그래픽스에서는 성능(속도)이 매우 중요합니다. 광원과 관찰자의 관계에 따라 일정한 결과를 도출할 수 없다면 매우 복잡한 공식이 필요해집니다.
예를 들어, [그림16]처럼 표면에 방향성 있는 미세한 결이 있다고 가정해봅시다.
[그림16. 서피스의 방향성 있는 미세한 결]
이런 표면에서는 [그림15]와 같은 Bidirectional 특성을 기대하기 어렵습니다. 사용자가 원하는 결과를 얻으려면 재질이나 기하학적 위치에 따라 다른 공식이 필요해집니다. 아티스트가 이를 모두 관리하기 어려울 뿐만 아니라, 공식이 복잡해지면서 성능도 저하됩니다.
하지만 PBR에서는 눈에 거의 보이지 않는 미세면(microfacet)을 고려하되, [그림16]처럼 특정 방향으로 쏠린 미세면이 아닙니다. 일정한 분포를 가진 미세면으로 이루어져 있습니다. 이를 "Microfacet Model"이라고 부르며, 나중에 자세히 다룰 것입니다.
일정한 분포를 가진 미세면을 고려하면 빛과 관찰자의 관계에 따른 반사율이 일관된 방식으로 정의됩니다. 즉, Bidirectional한 성격을 띠게 되며, 하나의 재질에 대해 빛과 관찰자의 관계에 따른 여러 공식을 가질 필요가 없어집니다.
P.S. "그렇다면 BRDF로 방향성을 가진 결을 만들 수는 없나요?"라는 질문을 할 수 있습니다. 물론 가능합니다. NormalMap 등을 사용하여 노멀(Normal)을 왜곡시킴으로써 결을 만들어낼 수 있습니다. 하지만 이는 '관찰자와 빛의 관계에 따라 일관된 결과가 나온다'는 BRDF의 대전제를 깨는 것은 아닙니다.http://googleusercontent.com/image_generation_content/19
PBR19. BRDF (양방향 반사율 분포 함수)
BRDF는 "Bidirectional Reflectance Distribution Function"의 약자로, 우리말로는 "양방향 반사율 분포 함수"입니다. BRDF는 크게 Diffuse BRDF와 Specular BRDF로 나뉩니다. 현재 모든 것을 한 번에 설명할 수 있는 완벽한 단일 모델은 상용화되어 있지 않습니다.
BRDF는 [그림1]의 파라미터들을 사용하여 식1과 같은 형태로 정의됩니다.
식1. BRDF 함수 형태
[그림1. BRDF 함수]
(이미지: 표면의 한 점에서 입사광 벡터(ωi)와 반사광 벡터(ωo)가 그려져 있음)
식이 복잡해 보일 수 있지만, 규칙을 알면 어렵지 않습니다.
•
r: 아래첨자 r은 'reflectance'(반사율)의 약자입니다. 이 함수가 반사율을 다룬다는 의미입니다.
•
ω (오메가): 함수의 입력값(매개변수)을 의미합니다.
◦
ωi: 'incident'(입사)의 약자로, 입사광 벡터(광원을 향하는 벡터)를 의미합니다.
◦
ωo: 'reflected'(반사)의 약자로, 반사광 벡터(관찰자를 향하는 벡터)를 의미합니다.
정리하면, BRDF 함수 f는 입사 방향(ωi)과 반사 방향(ωo)을 입력으로 받아, 그 관계에 따른 반사율(입사광과 반사광의 비율)을 출력합니다.
여기서 f는 실제 구체적인 식을 가지고 있지 않습니다. 단지 형태와 조건을 정의한 것입니다. 다음 조건을 만족하면 BRDF라고 할 수 있습니다.
•
반사율 분포(Reflectance Distribution)를 출력함.
•
양방향성(Bidirectional)을 가짐: 광원과 관찰자의 관계가 동일하면 반사율 분포가 변하지 않음.
•
광원과 관찰자를 입력 파라미터로 받음.
•
함수(Function)여야 함: 같은 입력에는 항상 같은 결과가 나와야 함.
이러한 조건을 만족하기만 하면 구현하는 사람마다 다른 결과를 낼 수 있습니다. 그래서 BRDF 모델은 매우 다양합니다([그림2] 참조).
[그림2. 다양한 BRDF 모델들]
[그림2]에는 Cook-Torrance, Oren-Nayar, Phong, Blinn 등 다양한 BRDF 모델들이 있습니다.
•
Theoretical (이론적): 이론적으로 더 올바른 결과를 내는 모델.
•
Empirical (경험적): 이론적 바탕은 덜하지만 실증된 결과를 반영한 모델.
•
Experimental (실험적): 실험적인 결과를 보여주는 모델.
또한, 살색은 Isotropic(등방성) 결과를, 녹색은 Anisotropic(비등방성) 결과를 의미합니다.
5. Diffuse BRDF (난반사 BRDF)
일반적으로 Diffuse BRDF는 Lambertian reflectance(램버트 반사율)를 사용합니다. 복잡한 모델들도 있지만, 디퓨즈 모델의 경우 큰 차이가 나지 않습니다.
램버트 반사율은 표면이 이상적인 확산 반사(무광 재질)를 보여준다고 가정합니다. 즉, 모든 방향으로 균일하게 빛을 반사한다는 것입니다.
[16. Reflection에 대한 잘못된 상식들]에서 언급했듯이, 디퓨즈는 빛이 표면에 흡수된 후 다시 방출되는 것이며, 재질의 색상을 보여줍니다.
[그림6. Diffuse의 발생 과정]
(이미지: 빛이 표면 아래로 침투하여 여러 번 산란된 후 다시 외부로 방출되는 과정)
빛이 표면에서 어떻게 튕겨 나갈지는 재질의 성분과 밀도에 따라 달라집니다. 컴퓨터는 이를 정확하게 계산하기 어렵습니다. 그래서 빛이 모든 방향으로 고르게 반사된다고 단순화합니다. 이것이 바로 램버트 반사율입니다(이런 표면을 Lambertian surface라고 부릅니다).
이를 그림으로 나타내면 [그림7]과 같습니다.
[그림7. Lambertian reflectance (붉은색이 diffuse)]
(이미지: 표면에서 붉은색 빛이 반구형으로 퍼져나가는 모습)
여기서 궁금증이 생길 수 있습니다: "모든 방향으로 고르게 반사한다고 했는데, 왜 [그림7]은 한쪽이 더 밝아 보이나?" 그렇다면 [그림8]처럼 모든 방향이 완전히 똑같이 밝은 것이 맞을까요?
[그림8. Lambertian reflectance (전방향으로 동일하게 반사)]
(이미지: 표면에서 빛이 모든 방향으로 완전히 동일하게 퍼져나가는 모습)
정답은 "두 그림 모두 맞다"입니다.
빛은 [그림8]처럼 표면에서 고르게 반사됩니다. 하지만 표면에 들어오는 빛의 양이 다릅니다. [5. 조도(illuminance) 측정]에서 표면의 기울기에 따라 받는 빛의 양이 달라진다고 했던 것을 기억하시나요? 표면에서 반사되는 빛은 [그림8]처럼 모든 방향으로 고르게 나가지만, 우리 눈으로 보면 [그림7]처럼 기울기에 따라 밝기가 다르게 보입니다. 램버트 모델에서는 보는 각도와 상관없이 반사율은 같지만, 들어오는 빛의 양 자체가 다르기 때문에 기울기가 커지면 어두워 보입니다.
[그림9. 기울기와 조도의 관계 (램버트 코사인 법칙)]
(이미지: 법선 벡터와 입사광 벡터의 각도가 커질수록 표면에 닿는 빛의 밀도가 줄어드는 다이어그램)
[그림9]에서 박스를 일정한 양의 빛이라고 생각해봅시다. 표면이 기울어지면 같은 면적이라도 더 적은 빛을 받습니다. 이것을 수학적으로 정리한 사람이 Lambert입니다. 그 결과가 코사인(cosine) 값과 같아서 램버트 코사인 법칙(Lambertian Cosine Law)이라고 부릅니다.
빛을 향하는 벡터(L)와 표면의 법선(N)을 내적하면 그 결과는 코사인 값과 같습니다. N과 L은 길이가 1인 벡터이기 때문입니다.
식2. Diffuse BRDF (램버트 코사인 법칙)
이것이 흔히 말하는 "엔닷엘(N·L)"입니다. N은 표면의 법선 벡터이고, L은 빛의 방향 벡터입니다.
여기서 의문이 생길 수 있습니다: "왜 식1의 f_r(ωi, ωo) 형태와 다른가?" 식2는 ωo(관찰자 위치)를 입력으로 받지 않습니다. 앞서 설명했듯이, [그림8]처럼 램버트 표면은 보는 위치와 상관없이 모든 방향으로 고르게 빛을 반사합니다. 그래서 관찰자의 위치는 필요하지 않습니다. ωo를 넣어도 결과가 바뀌지 않기 때문입니다. N·L은 들어오는 빛의 양을 계산하기 위한 것입니다.
6. 에너지 보존(Energy Conservation) 법칙
아티스트들과 연구자들은 이 Diffuse BRDF에 문제가 있다는 것을 발견했습니다(물리적으로 정확하지 않으면 자연스럽게 보이지도 않습니다. 우리 눈은 실제 세계의 물리 현상에 익숙하기 때문입니다).
무엇이 문제였을까요? 들어온 빛보다 나가는 빛이 더 많았습니다. 이것은 에너지가 무에서 생겨나는 것처럼 보이는 문제입니다.
[그림8]을 보면 빛이 모든 방향으로 나갑니다. 다른 방향으로 간 빛은 우리 눈에 들어오지 않습니다. 그런데 N·L은 이 다른 방향으로 가는 빛을 고려하지 않았습니다. 빛과 표면 법선의 관계만 계산했을 뿐입니다.
그래서 나가는 빛의 양을 모두 더한 다음, 그 값으로 나눠줍니다. 피자 한 판을 10조각으로 나누고 한 조각을 먹었다면, 내가 먹은 비율은 1/10입니다. 이와 비슷한 원리입니다. [7. Light Intensity 설정]에서 점광원의 빛 전체를 4π로 나눠야 정확한 값이 나온다고 했던 것을 기억하시나요? 같은 개념입니다.
이를 증명하려면 미적분이 필요하므로 여기서는 자세히 다루지 않겠습니다. 단순히 π로 나눠야 한다는 것만 알아두시면 됩니다. (자세한 유도 과정이 궁금하다면 [5]의 "Relating peak luminous intensity and luminous flux"를 참조하세요.)
최종 Diffuse BRDF 식은 식3과 같습니다. 이번에는 식1과 같은 형태로 정리했습니다.
식3. Diffuse BRDF (에너지 보존 법칙 고려)
따라서 PBR이 적용된 엔진에서는 Diffuse가 약 1/3 정도 어두워집니다(π는 약 3.14입니다).
우리는 Diffuse 맵(언리얼에서는 Base Texture)을 알베도(Albedo) 개념으로 사용합니다. 알베도는 절대적인 색상이 아니라 반사 비율을 의미합니다. 그러므로 PBR 환경에서는 Diffuse 맵의 밝기를 직접 조절하지 말고, 광원의 밝기 같은 다른 설정으로 밝기를 조정하는 것이 좋습니다.
PBR20. Specular BRDF (정반사 BRDF)
[19. Diffuse BRDF]에서 디퓨즈(Diffuse)는 램버트 코사인 법칙을 모든 재질에 동일하게 적용한다고 했습니다. 그래서 금속이 아니라면 디퓨즈는 모든 재질에서 거의 똑같이 동작합니다.
[그림1. Lambert 모델과 Burley 모델의 비교]
(이미지: Lambert 모델과 Burley 모델의 디퓨즈 결과 비교, 큰 차이가 없음)
디즈니의 Burley가 새로운 디퓨즈 모델을 만들었습니다. 하지만 [그림1]에서 보듯이 Lambert 모델과 겉으로 보기에는 큰 차이가 없습니다. 오히려 계산이 더 복잡해서 실시간 그래픽스에서는 잘 쓰이지 않습니다.
하지만 스페큘러(Specular, 반짝이는 하이라이트)는 다릅니다. 물체가 어떤 재질인지에 따라 스페큘러의 모양이 크게 달라집니다. 스페큘러는 물체의 재질을 보여주는 중요한 요소입니다. 여러분이 들어본 대부분의 BRDF 모델은 거의 다 스페큘러와 관련된 것입니다. 그래서 디퓨즈보다 계산이 조금 더 복잡하더라도 재질의 차이를 확실히 보여줄 수 있는 모델을 사용합니다.
지금까지 PBR의 기본 원칙들을 살펴보았습니다. 처음에 PBR에는 다음 요소들이 필요하다고 말했습니다.
•
전역 조명: IBL(이미지 기반 조명)
•
에너지 보존 법칙
•
반사도: 디퓨즈와 스페큘러
•
미세면: 러프니스(거칠기)
•
프레넬 법칙
•
금속성
이전 문서에서는 빛의 기본 성질, 에너지 보존 법칙, 전역 조명, 프레넬 법칙, 그리고 디퓨즈 BRDF를 다뤘습니다.
이제 마지막으로 이번 챕터에서는 미세면과 금속성을 다룹니다. 순서가 뒤죽박죽인 것처럼 보일 수 있지만, 나름의 흐름이 있습니다.
이제 PBR의 스페큘러 BRDF를 자세히 살펴보겠습니다.
MERL 100
디퓨즈 및 스페큘러 모델을 만들 때 아무렇게나 만드는 것은 아닙니다. 어떤 기준이 있어야 하며, 실제로 측정된 BRDF 모델을 사용하는 경우가 많습니다. 그중 하나가 MERL 100입니다.
[그림2. MERL 100]
(이미지: 다양한 재질의 BRDF 측정 샘플)
MERL 100은 100개의 등방성 재질(페인트, 나무, 금속, 섬유, 돌, 플라스틱 등)을 캡처한 데이터베이스입니다. 새로운 BRDF 모델이 나왔을 때 그 결과가 얼마나 실제와 일치하는지 확인하기 위한 **벤치마크(기준점)**로 사용됩니다. (이것을 반드시 이해할 필요는 없으며, 우리가 다루는 영역이 매우 물리적인 측정값에 기반하고 있음을 강조하기 위해 언급했습니다.)
1. 미세면 분포 함수(Distribution Function): D 함수
미세면(Microfacet) 모델은 폴리곤의 거대면(Macrosurface)이 [그림3]처럼 **미세면(Microsurface)**으로 구성되어 있다는 전제하에 반사나 굴절을 모델링하는 것을 의미합니다.
[그림3. Microsurface vs Macrosurface]
(이미지: 거대면(매끈한 표면)을 확대한 모습으로, 실제로는 수많은 미세한 면들로 이루어져 있음을 보여줌)
여러분은 반짝반짝 빛나는 면들은 매끈하고, 빛나지 않는 면들은 거칠다는 것을 경험적으로 알고 있을 것입니다(코팅 등으로 빛나는 경우는 제외).
하지만 이러한 미세면의 분포는 재질마다 다릅니다. 이를 알베도(Albedo) 설정하듯이 아티스트가 일일이 설정할 수는 없습니다. 게다가 미세면은 거의 눈에 보이지 않는 작은 면을 이야기합니다.
그러므로 몇 가지 매개변수만으로 분포를 계산할 수 있는 함수가 필요합니다. 그것이 바로 **미세면 분포 함수(Microfacet Distribution Function)**이며, 줄여서 D 함수라고 부릅니다. 일반적으로 이 D 함수는 통계적인 기법을 이용합니다.
이 D 함수는 스페큘러 하이라이트(Specular Peak)가 어느 방향을 향하게 되는지를 결정합니다. 우리는 스페큘러를 거울면 반사라고 생각하지만, 사실 입사각과 반사각이 정확히 일치하지 않을 수 있습니다. 이는 표면의 거칠기(미세면의 분포)에 영향을 받습니다. 거울면 반사에서 벗어나서 생기는 반사를 **"Off-specular reflection"**이라고 부릅니다.
[그림4. Off-specular reflection의 예]
(이미지: 표면의 거칠기에 따라 지표각에 가까워질수록 스페큘러의 방향(M)이 반사각과 달라지는 모습을 보여줌)
즉, D 함수는 거대면 내에서 우리에게 거울면 반사를 보여줄 수 있는 미세면의 양이 얼마나 되는지를 알려줍니다.
PBR Specular D의 기하학적 의미
PBR(Physically Based Rendering)에서 널리 사용되는 Cook-Torrance의 스페큘러(Specular) BRDF는 다음과 같이 정의됩니다.
[이미지: Cook-Torrance Specular BRDF 공식]
이 공식 중 D 함수는 미세면(microfacet) 기울기의 분산(Distribution) 함수입니다. 이 문서에서는 D 함수의 기하학적 의미를 설명합니다.
2. 미세면과 하프 벡터의 관계
PBR 이론의 핵심은 하나의 서피스(surface)가 여러 개의 미세면(microfacet)으로 구성되어 있다는 것입니다. 서피스를 구성하는 각 미세면은 서로 다른 노멀(normal)을 가지며, 거울면 반사(mirror reflection, 정반사)가 발생합니다.
많은 문서에서 미세면의 노멀을 m 또는 h로 표시합니다. 아마도 microfacet normal과 half vector의 약자인 것 같습니다. [그림1]은 서피스와 미세면의 관계를 보여줍니다.
[그림1. 미세면으로 구성된 서피스]
(이미지: 거친 표면을 확대한 모습으로, 작은 경사진 면들(미세면)이 모여 있음을 보여줌. 거대면의 노멀과 각 미세면의 노멀이 다름.)
미세면의 노멀을 m으로 표기하는 것은 직관적이지만, h(하프 벡터)로 표기할 수도 있다는 것은 언뜻 이해하기 어려울 수 있습니다. 하지만 Burley와 Cook-Torrance는 공통적으로 하프 벡터(half vector)가 미세면의 노멀을 표현한다고 설명합니다.
하프 벡터의 의미는 사용 맥락을 통해 이해하는 것이 좋습니다. 앞서 미세면이 거울면 반사를 보여준다고 가정했습니다. 이제 질문을 뒤집어 보죠.
"서피스 내에서 우리에게 거울면 반사를 보여줄 수 있는 기울기를 가진 미세면은 얼마나 많을까요?"
이것이 바로 Specular D 함수를 통해 얻고자 하는 값의 본질입니다. [그림2]의 가장 왼쪽 미세면이 거울면 반사를 보여주려면 어떤 기울기를 가져야 할까요? 여기서 n은 서피스 노멀이고 m은 미세면 노멀입니다.
[그림2. 샘플 미세면]
(이미지: 하나의 미세면이 그려져 있고, 빛 벡터(L), 뷰 벡터(V), 서피스 노멀(N), 미세면 노멀(m)이 표시되어 있음.)
거울면 반사는 "입사각과 반사각이 같은 반사"입니다. 따라서 아래 그림처럼 빛 벡터 l과 뷰 벡터 v의 절반인 하프 벡터(h)와 미세면 노멀(m)이 일치할 때 거울면 반사가 발생합니다.
[이미지: 하프 벡터(h)와 미세면 노멀(m)이 일치할 때 거울면 반사가 일어나는 다이어그램]
(이미지: 빛(l)과 뷰(v) 벡터 사이의 하프 벡터(h)가 미세면의 노멀(m)과 일치하는 상황을 보여줌.)
여기서 추론할 수 있는 것은, 뾰족한 미세면이 많으면 retroreflection(재귀반사)의 양이 많아진다는 것입니다. 무작위로 거칠면 난반사가 심해지고, 부드러우면(즉, m이 n과 거의 비슷한 면이 많으면) 정반사가 강해집니다.
결국 우리의 질문은 다음과 같이 바뀝니다.
"광원을 향하는 벡터 l과 관찰자(뷰)를 향하는 벡터 v가 주어졌을 때, 그 하프 벡터 h와 동일한 미세면 노멀 m은 얼마나 존재하나요?"
하프 벡터 h와 미세면 노멀 m의 각도가 0이 되는 미세면의 분포를 찾는 것이 Specular D 함수의 목적입니다. 따라서 일부 문헌에서는 이런 가정하에 "하프 벡터가 미세면의 노멀이다"라고 표현합니다.
Specular D 함수의 종류와 특징
[3]에서 Burley는 실측 데이터와 여러 Specular D 함수를 비교했습니다.
[그림3. Burley가 비교한 분포들]
(이미지: 실제 크롬의 반사 데이터(왼쪽)와 GGX, Beckmann 모델(오른쪽)을 비교한 그래프. GGX가 실제 데이터에 더 가까우나 완벽하지는 않음.)
왼쪽부터 실제 크롬 측정값, GGX 모델, Beckmann 모델의 결과입니다.
기존 모델 중에서는 GGX(Trowbridge-Reitz라고도 함)가 가장 좋았습니다. 그런데 실제 측정값을 보면 불타는 듯한 효과와 더 긴 꼬리 부분이 나타납니다. 그래서 Burley는 스페큘러 로브를 두 개 사용하는 방식을 만들었습니다.
하지만 실시간 렌더링에서는 계산을 두 번 하는 것이 너무 무겁습니다. 그래서 UE는 GGX만 사용합니다.
물론 다양한 변형 모델들이 있으며, Specular BRDF Reference에서 확인할 수 있습니다. 참고로 여기서 "Normal Distribution"은 통계의 정규분포가 아니라 "노멀 방향의 분포"를 뜻합니다. "Specular D"와 같은 의미입니다.
3. 미세면 그림자 함수(Geometry Function): G 함수
렌더링할 때 그림자가 없으면 매우 부자연스럽습니다. 미세면의 그림자는 큰 면의 그림자만큼 눈에 띄지는 않습니다. 거의 보이지 않기 때문에 "이 정도는 무시해도 되지 않을까?"라고 생각할 수 있습니다.
[그림5. 그림자 마스킹의 기하학]
(이미지: 미세면 사이에서 빛이 가려지거나 차폐되는 모습)
하지만! 에너지 보존 법칙을 위해서는 반드시 고려되어야 합니다. 미세면 그림자 마스킹도 아티스트가 작업할 수 있는 영역이 아니므로, 이것도 함수로 만듭니다. 기하(Geometry)와 관련된 것이므로 G 함수라고 부릅니다.
밑의 논문은 자세한 G함수에 대한 내용을 파악 할 수 있는 논문입니다.
4. 프레넬 함수(Fresnel Function): F 함수
모든 물체의 반사에는 프레넬 법칙이 적용된다고 했습니다. 당연히 이것과 관련된 함수도 있겠죠? 프레넬(Fresnel)의 머리글자를 따서 F 함수라고 부릅니다. (프레넬이 뭔지 기억이 가물가물하다면 [17. Fresnel이란] 문서를 참고하세요.)
일반적으로 금속일수록 거의 모든 각도에서 높은 반사율을 보이며, 비금속일수록 지표각(비스듬한 각도)에서 높은 반사율을 가집니다.
5. 세 가지 함수를 모아 봅시다
자, 위에서 언급한 세 개의 함수를 모아봅시다. 어떤 빛이 표면에 들어오면,
1.
미세면 분포 함수(D)에 의해 Off-specular reflection이 결정되고,
2.
기하학적 감쇠(G) 함수에 의해 에너지 보존 법칙이 적용되며,
3.
프레넬(F) 함수에 의해 반사율이 결정됩니다.
눈치가 빠른 분들은 D와 G가 표면의 **거칠기(Roughness)**와 관련이 있고, F가 **금속성(Metalicity)**과 관련이 있음을 알 수 있을 겁니다. 이를 제대로 표현하기 위해서는 복잡한 공식이 필요하지만, 여기서는 구체적으로 언급하지 않겠습니다.
그러므로 미세면과 프레넬을 고려한 Specular BRDF는 기본적으로 다음 식1과 같은 형태를 띱니다. 분모에 우리가 언급하지 않은 항들이 있지만, 이는 빛과 표면의 관계 및 에너지 보존을 위해 들어간 것이므로 크게 신경 쓸 필요는 없습니다.
식1. Specular BRDF (Cook-Torrance 모델)
식1은 Cook-Torrance의 BRDF 모델이며, D, F, G를 위해 어떤 알고리즘을 사용하느냐에 따라 결과가 조금씩 달라집니다. UE4의 경우, D를 위해 GGX, G를 위해 Smith Approximation, F를 위해 Schlick's approximation을 사용합니다.
여기서 식을 굳이 이해할 필요는 없습니다. 위에서 언급했듯이 Roughness 값은 D와 G에 영향을 주고, Metalicity 값은 F에 영향을 준다는 것만 알고 있으면 됩니다.
•
Roughness: 반사의 선명도 및 확산과 관련이 있습니다.
•
Metalicity: 반사의 세기 및 각도(프레넬)와 관련이 있습니다.
6. UE에서의 Metallic
UE에서의 Metallic은 프레넬과 관련이 있다고 했습니다. 정확히 말하자면 **F0 값(0도 입사각에서의 기본 반사율)**입니다. 이는 굴절률(Index Of Refraction, IOR) 값으로부터 결정됩니다. (기억이 나지 않는다면 [17. Fresnel이란]을 참고하세요.)
[그림6. 프레넬 공식 그래프]
(이미지: 0도에서 반사율이 F0부터 시작하여 지표각으로 갈수록 1에 가까워지는 그래프)
•
금속: 수직으로 내려다봤을 때(0도) 0.5 이상의 F0 값을 가집니다.
•
보석: 0.2 이하의 F0 값을 가집니다.
•
자연의 많은 물체(비금속): 0.05 이하의 F0 값을 가집니다.
F0 값이 낮을수록 지표각에 가까워져야 반사가 제대로 보입니다. 이 F0 값이 Metallic 값으로 사용됩니다. 즉, 높은 Metallic 값을 가진다면 아무 데서나 봐도 반사가 잘 보이고, 낮은 Metallic 값을 가진다면 지표각에 가까워야 반사가 잘 보인다는 의미입니다.
7. 언리얼 엔진의 SpecularColor (반짝이는 색상)
언리얼 엔진에서 SpecularColor가 무엇인지 알아봅시다. 원래 SpecularColor는 물체의 색이 아니라 빛의 색을 말합니다. 하지만 Metallic 값이 정확히 0이나 1인 경우는 드물기 때문에, 실제로는 빛의 색과 물체의 색이 섞입니다.
금속은 빛을 모두 흡수했다가 다시 내보냅니다. 그래서 금속에는 디퓨즈(확산광)가 없고, 스페큘러(반사광)만 있으며 금속 고유의 색이 나타납니다. 그런데 SpecularColor를 별도로 설정하면 성능과 메모리에 부담이 되므로, 언리얼 엔진 4에서는 BaseColor를 금속의 반사 색상처럼 사용합니다.
언리얼 엔진 4는 다음 공식으로 SpecularColor와 DiffuseColor를 계산합니다.
이 공식은 lerp 함수를 사용합니다. lerp(x, y, z)는 x와 y 사이의 값을 z에 따라 섞어줍니다. z가 0이면 x가 나오고, z가 1이면 y가 나옵니다.
•
완전한 금속(Metallic = 1): BaseColor를 반사 색상으로 사용합니다.
•
완전한 비금속(Metallic = 0): 0.08 * Specular.xxx를 반사 색상으로 사용합니다.
xxx는 같은 값을 RGB 세 채널 모두에 넣는다는 뜻입니다. 즉, Specular는 색상(컬러)이 아니라 하나의 숫자 값입니다.
[그림7. Material Specular 핀]
(이미지: 언리얼 엔진 Material Editor의 Specular 핀)
여기에 컬러를 넣는 분들이 있는데, 이름이 "Specular Color"가 아니라 "Specular"인 이유가 있습니다. 숫자 값만 받기 때문에 컬러를 넣으면 빨간색(R) 값만 사용됩니다([그림8] 참조).
[그림8. 잘못된 Specular 값 설정]
(이미지: Specular 핀에 컬러를 넣었을 때 R 채널만 사용되는 예시)
Specular 값에 0.08이 곱해지므로 매우 작은 값이 됩니다. 기본값이 0.5이므로, 실제로는 0.04가 됩니다. 즉, Metallic이 0이어도 반사광이 약 4% 정도 나타납니다.
lerp 공식에 따라 SpecularColor는 다음과 같이 변합니다.
Metallic | 공식 | 결과 |
0 | 0.08 * Specular.xxx * (1-0) + BaseColor.xyz * 0 | 0.08 * Specular.xxx |
0.3 | 0.08 * Specular.xxx * (1-0.3) + BaseColor.xyz * 0.3 | 0.056 * Specular.xxx + 0.3 * BaseColor.xyz |
0.6 | 0.08 * Specular.xxx * (1-0.6) + BaseColor.xyz * 0.6 | 0.032 * Specular.xxx + 0.6 * BaseColor.xyz |
1.0 | 0.08 * Specular.xxx * (1-1) + BaseColor.xyz * 1 | BaseColor.xyz |
BaseColor는 RGB 전체를 사용하고 Specular는 회색조입니다. 따라서 Metallic이 1에 가까우면 반사 색상에 BaseColor가 많이 섞이고, 0에 가까우면 BaseColor가 적게 섞입니다. BaseColor가 적게 섞인다는 것은 순수한 빛의 색에 가깝다는 뜻입니다. 대신 Specular에 0.08이 곱해져서 반사가 약해집니다.
[그림9. Metallic에 따른 Specular Color 변화 (Diffuse Off)]
(이미지: Metallic 값에 따라 SpecularColor가 BaseColor와 광원 색상 사이에서 보간되는 모습)
흰색 빛에서는 차이가 잘 안 보이니, 보라색 빛을 추가해 봅시다.
[그림10. 색상이 있는 광원을 추가했을 때의 결과 (Diffuse Off)]
(이미지: Metallic 값이 낮을수록 광원(보라색)의 색상이 Specular Color에 더 많이 반영됨)
[그림10]을 보면 Metallic이 낮을수록 빛의 원래 색이 반사에 더 많이 나타난다는 것을 확실히 알 수 있습니다.
비금속에서 반사의 강도를 조절하고 싶다면 "Specular" 핀을 사용하면 됩니다([그림11] 참조).
[그림11. Metallic = 0일 때 Specular 설정 결과 비교 (Diffuse Off)]
(이미지: Metallic이 0인 상태에서 Specular 핀의 값을 조절하여 하이라이트 세기가 변하는 모습)
비금속 재질에서 반사에 빛의 색을 그대로 유지하고 싶다면, 프로그래머에게 SpecularColor 공식을 수정해 달라고 요청하면 됩니다.
[그림11. Metallic = 0일 때 Specular 설정 결과 비교 (Diffuse Off)]
8. 언리얼 엔진 4의 Roughness
Roughness는 눈으로 보기에 가장 쉽게 이해할 수 있습니다. 내부적으로는 복잡한 계산에 사용되지만, 아티스트는 크게 신경 쓸 필요가 없습니다.
"거칠면 반사가 흐릿해지고, 매끄러우면 반사가 선명해진다"고 이해하면 됩니다.
[그림12. Metallic이 0.5일 때 Roughness 변화에 의한 결과 (Diffuse Off)]
(이미지: Roughness 값이 낮을수록 반사가 선명하고, 높을수록 뭉개지는 모습)
"거칠면 반사가 흐릿해지고, 매끄러우면 반사가 선명해진다"고 이해하면 됩니다.
9. 에너지 보존 법칙 (확산광과 반사광의 관계)
앞에서 에너지 보존 법칙을 언급했습니다. 여기서는 확산광(디퓨즈)과 반사광(스페큘러)의 관계에서 에너지 보존 법칙을 설명하겠습니다.
표면에 들어온 빛은 일부는 흡수되고, 일부는 반사되고, 일부는 통과합니다. 반사되는 빛은 확산광과 반사광으로 나뉩니다. 문제는 확산광과 반사광이 어떤 비율로 나뉘느냐입니다. 예전 방식에서는 작업자가 값을 직접 설정했습니다. 그러다 보니 원하는 결과를 만들려고 너무 많은 빛을 넣는 경우가 많았습니다.
조명을 잘 모르면 적절한 값을 설정하기 어렵고, 특히 여러 가지 조명이 있는 장면에서 맞추기는 더 어렵습니다.
[그림13. 에너지 보존을 적용하지 않은 경우]
(이미지: 가장 왼쪽은 과도하게 빛나고 가장 오른쪽은 선명하지 않은 결과)
[그림14. 에너지 보존 법칙이 적용된 경우]
(이미지: 물리적으로 올바른 에너지 보존이 적용된 결과)
하지만 PBR에서는 나가는 빛이 들어온 빛보다 많으면 안 됩니다. 빛이 흡수되거나 통과하지 않는다고 가정하면, 확산광 + 반사광의 양은 항상 들어온 빛의 양과 같아야 합니다. 그래서 언리얼 엔진에서는 Metallic 값으로 확산광의 양을 조절합니다.
DiffuseColor = BaseColor - BaseColor * Metallic;
Metallic이 커지면 반사광이 강해지고, 확산광은 줄어듭니다. 위에서 SpecularColor를 계산할 때 Metallic.xxx를 사용하기 때문에, Metallic이 크면 반사광이 늘어나고 Metallic이 작으면 확산광이 늘어납니다.
기존 방식에 익숙한 분들은 이게 어색할 수 있지만, 물리적으로 정확한 방법입니다. 조명 환경이 바뀌어도 자연스럽고, 작업자가 비율을 일일이 신경 쓰지 않아도 되니 매우 편리합니다.
DiffuseColor = BaseColor - BaseColor * Metallic;
21. 렌더링 방정식
제시된 이미지는 반사 방정식(Reflectance Equation), 또는 렌더링 방정식(Rendering Equation)의 구체적인 형태를 나타냅니다. 이 수식은 표면의 한 지점에서 특정 방향으로 반사되어 나가는 빛의 총량을 계산하는 데 사용됩니다.
수식의 각 항에 대한 상세 설명은 다음과 같습니다.
1. 좌변
•
(Outgoing Radiance):
◦
표면의 한 지점에서 관찰자(카메라) 방향 로 나가는 빛의 방사 휘도(Radiance)입니다.
◦
최종적으로 픽셀의 색상을 결정하는 값입니다.
2. 우변 (적분 내부)
•
(Integral over the Hemisphere):
◦
표면 법선(Normal)을 중심으로 한 반구(Hemisphere, ) 영역 전체에 대해 적분한다는 의미입니다.
◦
현실 세계에서는 빛이 단일 방향이 아닌 사방에서 들어오므로, 표면 위쪽의 모든 방향에서 들어오는 빛을 합산해야 합니다.
•
(BRDF):
◦
양방향 반사 분포 함수(Bidirectional Reflectance Distribution Function)입니다.
◦
입사 방향 에서 들어온 빛이 관찰 방향 로 얼마나 반사되는지 비율을 결정합니다.
◦
물체의 재질(거칠기, 금속성 등)을 정의하는 핵심 함수입니다.
•
(Component-wise Multiplication):
◦
성분별 곱셈을 의미합니다.
◦
컴퓨터 그래픽스에서 빛과 BRDF는 단일 스칼라 값이 아닌 RGB 벡터(Red, Green, Blue)로 표현되므로, 각 색상 채널끼리 별도로 곱셈이 수행됨을 명시합니다.
•
(Incoming Radiance):
◦
방향 에서 표면으로 들어오는 빛의 방사 휘도입니다.
◦
광원(Light Source)에서 직접 오는 빛일 수도 있고, 다른 물체에 반사되어 들어오는 간접광(Indirect Light)일 수도 있습니다.
•
(Cosine Term / Lambert's Cosine Law):
◦
표면 법선 벡터 과 입사 조명 벡터 의 내적(Dot Product)입니다.
◦
입사각의 코사인() 값과 같습니다.
◦
빛이 표면에 비스듬히 들어올수록 단위 면적당 도달하는 빛의 에너지가 감소하는 기하학적 감쇠 현상을 반영합니다.
반사광 계산 공식은 복잡하지만, 아티스트는 Metallic과 Roughness 두 가지만 알면 됩니다. 이 두 값으로 대부분의 재질을 표현할 수 있습니다. 각 재질의 올바른 값은 이미 정해져 있으니, 이를 정리해서 자료로 만들어 두면 작업이 훨씬 쉬워집니다.
Metallic은 간단합니다. 비금속은 0, 금속은 1로 설정하면 됩니다. 실제로 중요한 것은 Roughness입니다. 특수한 경우(여러 재질이 섞인 경우)가 아니면 Metallic에 많은 용량을 쓸 필요가 없습니다. Metallic 맵은 보통 거의 한 가지 색입니다. 텍스처를 따로 만든다면 Metallic 맵만 작은 크기로 만들어도 충분합니다. 이렇게 하면 최적화에도 도움이 됩니다.
참고문헌





















.png&blockId=2ad0b1ff-a61e-80d1-82d0-c27bb8d27418)











.png&blockId=2ad0b1ff-a61e-80fc-b227-e5c27fb9c12b)




















.gif&blockId=2af0b1ff-a61e-80af-95fd-db7cdd76bfc4)










.jpg&blockId=2af0b1ff-a61e-80b8-866f-d2dd647f2827)




.png&blockId=2af0b1ff-a61e-803b-881d-fb381332e6d8)



.gif&blockId=2af0b1ff-a61e-807e-abe4-f70c1a6d28f2)

.png&blockId=2af0b1ff-a61e-806e-a9c6-fc95a115bad9)
.png&blockId=2af0b1ff-a61e-808c-a871-c0702dfda683)
.png&blockId=2af0b1ff-a61e-8086-a5bd-de4d5e45c7d7)